Equivariant Frames and the Impossibility of Continuous Canonicalization

Canonicalization provides an architecture-agnostic method for enforcing equivariance, with generalizations such as frame-averaging recently gaining prominence as a lightweight and flexible alternative to equivariant architectures. Recent works have found an empirical benefit to using probabilistic frames instead, which learn weighted distributions over group elements. In this work, we provide strong theoretical justification for this phenomenon: for commonly-used groups, there is no efficiently computable choice of frame that preserves continuity of the function being averaged. In other words, unweighted frame-averaging can turn a smooth, non-symmetric function into a discontinuous, symmetric function. To address this fundamental robustness problem, we formally define and construct \emph{weighted} frames, which provably preserve continuity, and demonstrate their utility by constructing efficient and continuous weighted frames for the actions of $SO(2)$, $SO(3)$, and $S_n$ on point clouds.

On the hardness of learning under symmetries

We study the problem of learning equivariant neural networks via gradient descent. The incorporation of known symmetries ("equivariance") into neural nets has empirically improved the performance of learning pipelines, in domains ranging from biology to computer vision. However, a rich yet separate line of learning theoretic research has demonstrated that actually learning shallow, fully-connected (i.e. non-symmetric) networks has exponential complexity in the correlational statistical query (CSQ) model, a framework encompassing gradient descent. In this work, we ask: are known problem symmetries sufficient to alleviate the fundamental hardness of learning neural nets with gradient descent? We answer this question in the negative. In particular, we give lower bounds for shallow graph neural networks, convolutional networks, invariant polynomials, and frame-averaged networks for permutation subgroups, which all scale either superpolynomially or exponentially in the relevant input dimension. Therefore, in spite of the significant inductive bias imparted via symmetry, actually learning the complete classes of functions represented by equivariant neural networks via gradient descent remains hard.

Learning Polynomial Problems with $SL(2,\mathbb{R})$ Equivariance

Optimizing and certifying the positivity of polynomials are fundamental primitives across mathematics and engineering applications, from dynamical systems to operations research. However, solving these problems in practice requires large semidefinite programs, with poor scaling in dimension and degree. In this work, we demonstrate for the first time that neural networks can effectively solve such problems in a data-driven fashion, achieving tenfold speedups while retaining high accuracy. Moreover, we observe that these polynomial learning problems are equivariant to the non-compact group $SL(2,\mathbb{R})$, which consists of area-preserving linear transformations. We therefore adapt our learning pipelines to accommodate this structure, including data augmentation, a new $SL(2,\mathbb{R})$-equivariant architecture, and an architecture equivariant with respect to its maximal compact subgroup, $SO(2, \mathbb{R})$. Surprisingly, the most successful approaches in practice do not enforce equivariance to the entire group, which we prove arises from an unusual lack of architecture universality for $SL(2,\mathbb{R})$ in particular. A consequence of this result, which is of independent interest, is that there exists an equivariant function for which there is no sequence of equivariant polynomials multiplied by arbitrary invariants that approximates the original function. This is a rare example of a symmetric problem where data augmentation outperforms a fully equivariant architecture, and provides interesting lessons in both theory and practice for other problems with non-compact symmetries.

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

Self-Supervised Learning with Lie Symmetries for Partial Differential Equations

Machine learning for differential equations paves the way for computationally efficient alternatives to numerical solvers, with potentially broad impacts in science and engineering. Though current algorithms typically require simulated training data tailored to a given setting, one may instead wish to learn useful information from heterogeneous sources, or from real dynamical systems observations that are messy or incomplete. In this work, we learn general-purpose representations of PDEs from heterogeneous data by implementing joint embedding methods for self-supervised learning (SSL), a framework for unsupervised representation learning that has had notable success in computer vision. Our representation outperforms baseline approaches to invariant tasks, such as regressing the coefficients of a PDE, while also improving the time-stepping performance of neural solvers. We hope that our proposed methodology will prove useful in the eventual development of general-purpose foundation models for PDEs.

GULP: a prediction-based metric between representations

Comparing the representations learned by different neural networks has recently emerged as a key tool to understand various architectures and ultimately optimize them. In this work, we introduce GULP, a family of distance measures between representations that is explicitly motivated by downstream predictive tasks. By construction, GULP provides uniform control over the difference in prediction performance between two representations, with respect to regularized linear prediction tasks. Moreover, it satisfies several desirable structural properties, such as the triangle inequality and invariance under orthogonal transformations, and thus lends itself to data embedding and visualization. We extensively evaluate GULP relative to other methods, and demonstrate that it correctly differentiates between architecture families, converges over the course of training, and captures generalization performance on downstream linear tasks.

Distilling Model Failures as Directions in Latent Space

Existing methods for isolating hard subpopulations and spurious correlations in datasets often require human intervention. This can make these methods labor-intensive and dataset-specific. To address these shortcomings, we present a scalable method for automatically distilling a model's failure modes. Specifically, we harness linear classifiers to identify consistent error patterns, and, in turn, induce a natural representation of these failure modes as directions within the feature space. We demonstrate that this framework allows us to discover and automatically caption challenging subpopulations within the training dataset, and intervene to improve the model's performance on these subpopulations. Code available at https://github.com/MadryLab/failure-directions

Implicit Bias of Linear Equivariant Networks

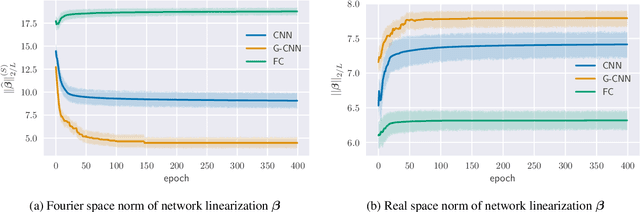
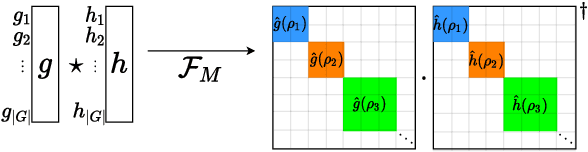
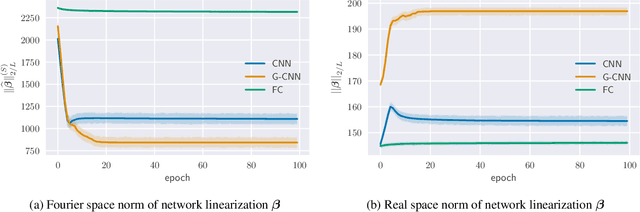
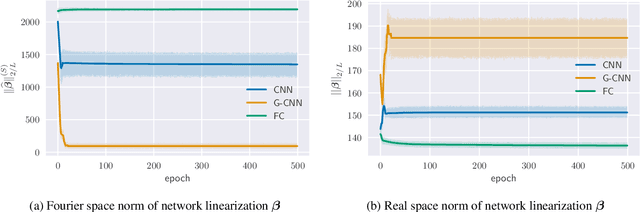
Group equivariant convolutional neural networks (G-CNNs) are generalizations of convolutional neural networks (CNNs) which excel in a wide range of scientific and technical applications by explicitly encoding group symmetries, such as rotations and permutations, in their architectures. Although the success of G-CNNs is driven by the explicit symmetry bias of their convolutional architecture, a recent line of work has proposed that the implicit bias of training algorithms on a particular parameterization (or architecture) is key to understanding generalization for overparameterized neural nets. In this context, we show that $L$-layer full-width linear G-CNNs trained via gradient descent in a binary classification task converge to solutions with low-rank Fourier matrix coefficients, regularized by the $2/L$-Schatten matrix norm. Our work strictly generalizes previous analysis on the implicit bias of linear CNNs to linear G-CNNs over all finite groups, including the challenging setting of non-commutative symmetry groups (such as permutations). We validate our theorems via experiments on a variety of groups and empirically explore more realistic nonlinear networks, which locally capture similar regularization patterns. Finally, we provide intuitive interpretations of our Fourier space implicit regularization results in real space via uncertainty principles.

Phase Retrieval with Holography and Untrained Priors: Tackling the Challenges of Low-Photon Nanoscale Imaging

Phase retrieval is the inverse problem of recovering a signal from magnitude-only Fourier measurements, and underlies numerous imaging modalities, such as Coherent Diffraction Imaging (CDI). A variant of this setup, known as holography, includes a reference object that is placed adjacent to the specimen of interest before measurements are collected. The resulting inverse problem, known as holographic phase retrieval, is well-known to have improved problem conditioning relative to the original. This innovation, i.e. Holographic CDI, becomes crucial at the nanoscale, where imaging specimens such as viruses, proteins, and crystals require low-photon measurements. This data is highly corrupted by Poisson shot noise, and often lacks low-frequency content as well. In this work, we introduce a dataset-free deep learning framework for holographic phase retrieval adapted to these challenges. The key ingredients of our approach are the explicit and flexible incorporation of the physical forward model into an automatic differentiation procedure, the Poisson log-likelihood objective function, and an optional untrained deep image prior. We perform extensive evaluation under realistic conditions. Compared to competing classical methods, our method recovers signal from higher noise levels and is more resilient to suboptimal reference design, as well as to large missing regions of low frequencies in the observations. To the best of our knowledge, this is the first work to consider a dataset-free machine learning approach for holographic phase retrieval.