Towards Low-Photon Nanoscale Imaging: Holographic Phase Retrieval via Maximum Likelihood Optimization

A new algorithmic framework is presented for holographic phase retrieval via maximum likelihood optimization, which allows for practical and robust image reconstruction. This framework is especially well-suited for holographic coherent diffraction imaging in the \textit{low-photon regime}, where data is highly corrupted by Poisson shot noise. Thus, this methodology provides a viable solution towards the advent of \textit{low-photon nanoscale imaging}, which is a fundamental challenge facing the current state of imaging technologies. Practical optimization algorithms are derived and implemented, and extensive numerical simulations demonstrate significantly improved image reconstruction versus the leading algorithms currently in use. Further experiments compare the performance of popular holographic reference geometries to determine the optimal combined physical setup and algorithm pipeline for practical implementation. Additional features of these methods are also demonstrated, which allow for fewer experimental constraints.

Phase Retrieval with Holography and Untrained Priors: Tackling the Challenges of Low-Photon Nanoscale Imaging

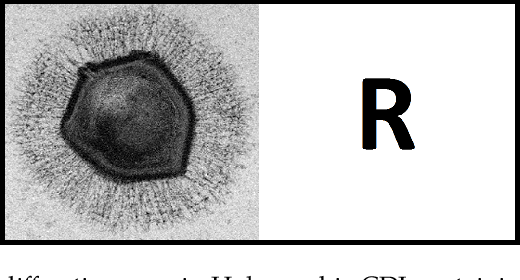
Phase retrieval is the inverse problem of recovering a signal from magnitude-only Fourier measurements, and underlies numerous imaging modalities, such as Coherent Diffraction Imaging (CDI). A variant of this setup, known as holography, includes a reference object that is placed adjacent to the specimen of interest before measurements are collected. The resulting inverse problem, known as holographic phase retrieval, is well-known to have improved problem conditioning relative to the original. This innovation, i.e. Holographic CDI, becomes crucial at the nanoscale, where imaging specimens such as viruses, proteins, and crystals require low-photon measurements. This data is highly corrupted by Poisson shot noise, and often lacks low-frequency content as well. In this work, we introduce a dataset-free deep learning framework for holographic phase retrieval adapted to these challenges. The key ingredients of our approach are the explicit and flexible incorporation of the physical forward model into an automatic differentiation procedure, the Poisson log-likelihood objective function, and an optional untrained deep image prior. We perform extensive evaluation under realistic conditions. Compared to competing classical methods, our method recovers signal from higher noise levels and is more resilient to suboptimal reference design, as well as to large missing regions of low frequencies in the observations. To the best of our knowledge, this is the first work to consider a dataset-free machine learning approach for holographic phase retrieval.

Dual-Reference Design for Holographic Coherent Diffraction Imaging

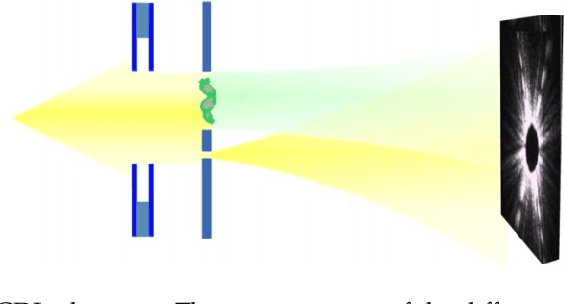
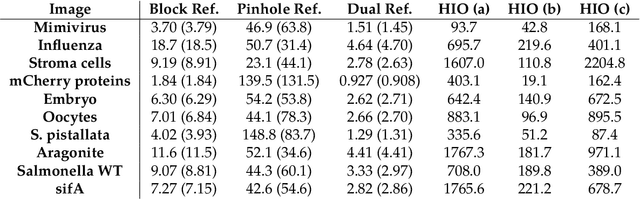
A new reference design is introduced for Holographic Coherent Diffraction Imaging. This consists of two reference portions - being "block" and "pinhole" shaped regions - adjacent to the imaging specimen. Expected error analysis on data following a Poisson shot noise model shows that the dual-reference scheme produces smaller weighting of error across the frequency spectrum than does the leading single-reference schemes. Numerical experiments on simulated data also shows the dual-reference scheme achieving a smaller recovery error than the leading single-reference schemes.