On the hardness of learning under symmetries

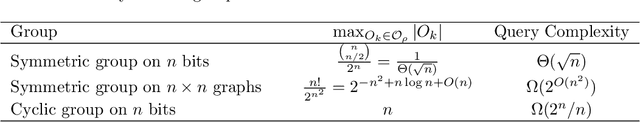
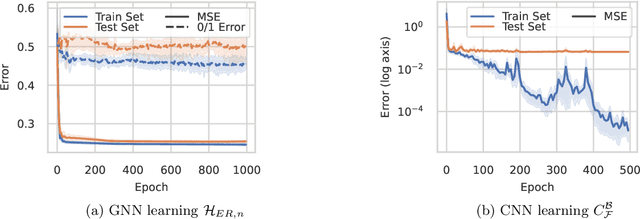
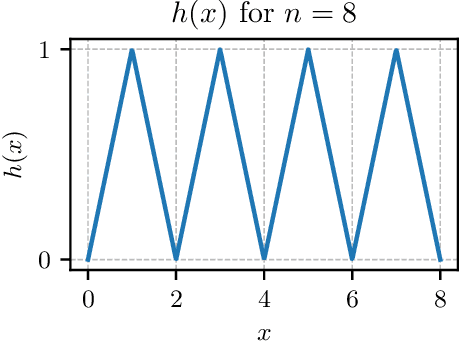
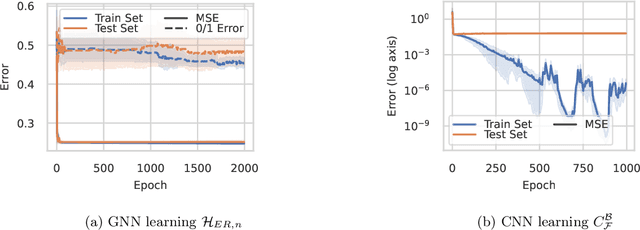
We study the problem of learning equivariant neural networks via gradient descent. The incorporation of known symmetries ("equivariance") into neural nets has empirically improved the performance of learning pipelines, in domains ranging from biology to computer vision. However, a rich yet separate line of learning theoretic research has demonstrated that actually learning shallow, fully-connected (i.e. non-symmetric) networks has exponential complexity in the correlational statistical query (CSQ) model, a framework encompassing gradient descent. In this work, we ask: are known problem symmetries sufficient to alleviate the fundamental hardness of learning neural nets with gradient descent? We answer this question in the negative. In particular, we give lower bounds for shallow graph neural networks, convolutional networks, invariant polynomials, and frame-averaged networks for permutation subgroups, which all scale either superpolynomially or exponentially in the relevant input dimension. Therefore, in spite of the significant inductive bias imparted via symmetry, actually learning the complete classes of functions represented by equivariant neural networks via gradient descent remains hard.

A Poincaré Inequality and Consistency Results for Signal Sampling on Large Graphs

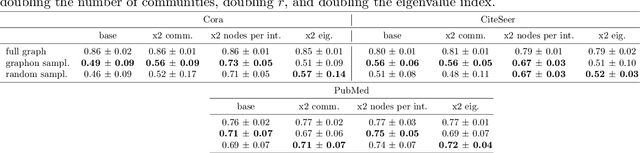
Large-scale graph machine learning is challenging as the complexity of learning models scales with the graph size. Subsampling the graph is a viable alternative, but sampling on graphs is nontrivial as graphs are non-Euclidean. Existing graph sampling techniques require not only computing the spectra of large matrices but also repeating these computations when the graph changes, e.g., grows. In this paper, we introduce a signal sampling theory for a type of graph limit -- the graphon. We prove a Poincar\'e inequality for graphon signals and show that complements of node subsets satisfying this inequality are unique sampling sets for Paley-Wiener spaces of graphon signals. Exploiting connections with spectral clustering and Gaussian elimination, we prove that such sampling sets are consistent in the sense that unique sampling sets on a convergent graph sequence converge to unique sampling sets on the graphon. We then propose a related graphon signal sampling algorithm for large graphs, and demonstrate its good empirical performance on graph machine learning tasks.

Limits, approximation and size transferability for GNNs on sparse graphs via graphops

Can graph neural networks generalize to graphs that are different from the graphs they were trained on, e.g., in size? In this work, we study this question from a theoretical perspective. While recent work established such transferability and approximation results via graph limits, e.g., via graphons, these only apply non-trivially to dense graphs. To include frequently encountered sparse graphs such as bounded-degree or power law graphs, we take a perspective of taking limits of operators derived from graphs, such as the aggregation operation that makes up GNNs. This leads to the recently introduced limit notion of graphops (Backhausz and Szegedy, 2022). We demonstrate how the operator perspective allows us to develop quantitative bounds on the distance between a finite GNN and its limit on an infinite graph, as well as the distance between the GNN on graphs of different sizes that share structural properties, under a regularity assumption verified for various graph sequences. Our results hold for dense and sparse graphs, and various notions of graph limits.

Training invariances and the low-rank phenomenon: beyond linear networks

The implicit bias induced by the training of neural networks has become a topic of rigorous study. In the limit of gradient flow and gradient descent with appropriate step size, it has been shown that when one trains a deep linear network with logistic or exponential loss on linearly separable data, the weights converge to rank-$1$ matrices. In this paper, we extend this theoretical result to the much wider class of nonlinear ReLU-activated feedforward networks containing fully-connected layers and skip connections. To the best of our knowledge, this is the first time a low-rank phenomenon is proven rigorously for these architectures, and it reflects empirical results in the literature. The proof relies on specific local training invariances, sometimes referred to as alignment, which we show to hold for a wide set of ReLU architectures. Our proof relies on a specific decomposition of the network into a multilinear function and another ReLU network whose weights are constant under a certain parameter directional convergence.