Implicit Bias of Linear Equivariant Networks
Paper and Code
Oct 12, 2021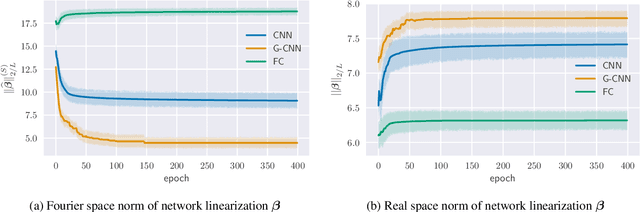
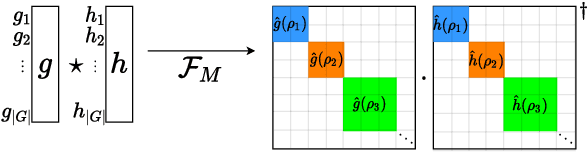
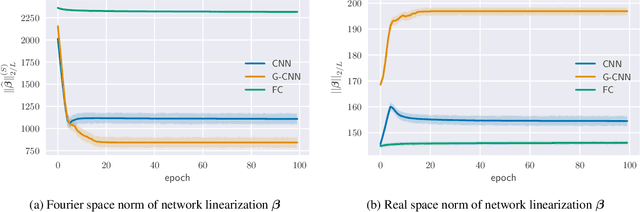
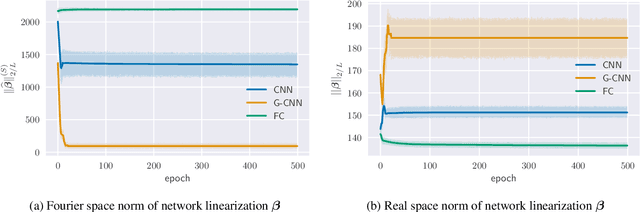
Group equivariant convolutional neural networks (G-CNNs) are generalizations of convolutional neural networks (CNNs) which excel in a wide range of scientific and technical applications by explicitly encoding group symmetries, such as rotations and permutations, in their architectures. Although the success of G-CNNs is driven by the explicit symmetry bias of their convolutional architecture, a recent line of work has proposed that the implicit bias of training algorithms on a particular parameterization (or architecture) is key to understanding generalization for overparameterized neural nets. In this context, we show that $L$-layer full-width linear G-CNNs trained via gradient descent in a binary classification task converge to solutions with low-rank Fourier matrix coefficients, regularized by the $2/L$-Schatten matrix norm. Our work strictly generalizes previous analysis on the implicit bias of linear CNNs to linear G-CNNs over all finite groups, including the challenging setting of non-commutative symmetry groups (such as permutations). We validate our theorems via experiments on a variety of groups and empirically explore more realistic nonlinear networks, which locally capture similar regularization patterns. Finally, we provide intuitive interpretations of our Fourier space implicit regularization results in real space via uncertainty principles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge