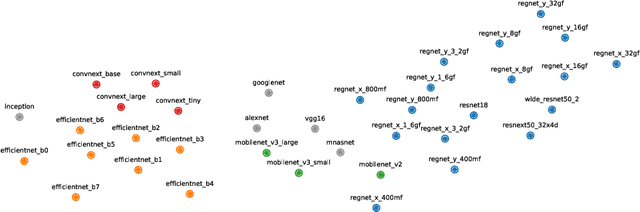
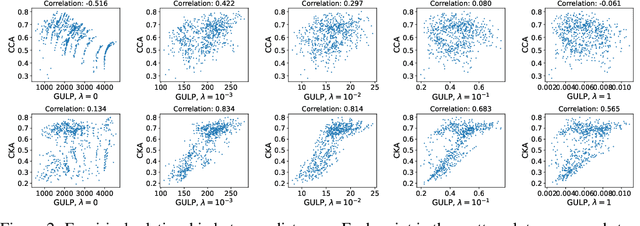
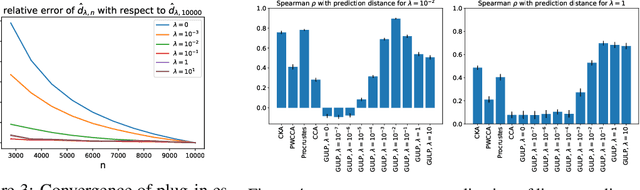
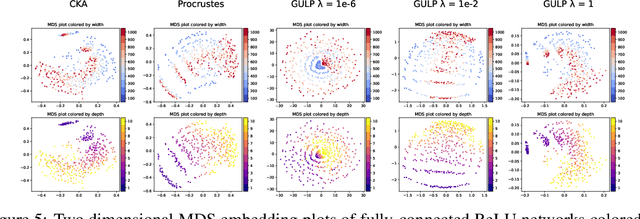
Comparing the representations learned by different neural networks has recently emerged as a key tool to understand various architectures and ultimately optimize them. In this work, we introduce GULP, a family of distance measures between representations that is explicitly motivated by downstream predictive tasks. By construction, GULP provides uniform control over the difference in prediction performance between two representations, with respect to regularized linear prediction tasks. Moreover, it satisfies several desirable structural properties, such as the triangle inequality and invariance under orthogonal transformations, and thus lends itself to data embedding and visualization. We extensively evaluate GULP relative to other methods, and demonstrate that it correctly differentiates between architecture families, converges over the course of training, and captures generalization performance on downstream linear tasks.

GULP: a prediction-based metric between representations