Improving Equivariant Networks with Probabilistic Symmetry Breaking

Equivariance encodes known symmetries into neural networks, often enhancing generalization. However, equivariant networks cannot break symmetries: the output of an equivariant network must, by definition, have at least the same self-symmetries as the input. This poses an important problem, both (1) for prediction tasks on domains where self-symmetries are common, and (2) for generative models, which must break symmetries in order to reconstruct from highly symmetric latent spaces. This fundamental limitation can be addressed by considering equivariant conditional distributions, instead of equivariant functions. We present novel theoretical results that establish necessary and sufficient conditions for representing such distributions. Concretely, this representation provides a practical framework for breaking symmetries in any equivariant network via randomized canonicalization. Our method, SymPE (Symmetry-breaking Positional Encodings), admits a simple interpretation in terms of positional encodings. This approach expands the representational power of equivariant networks while retaining the inductive bias of symmetry, which we justify through generalization bounds. Experimental results demonstrate that SymPE significantly improves performance of group-equivariant and graph neural networks across diffusion models for graphs, graph autoencoders, and lattice spin system modeling.

On the Identifiability of Causal Abstractions

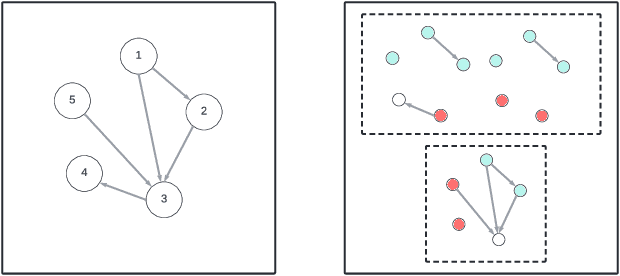
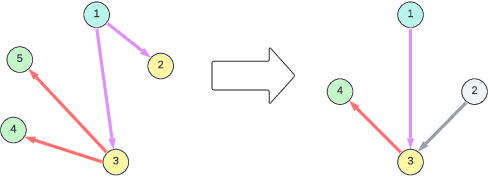
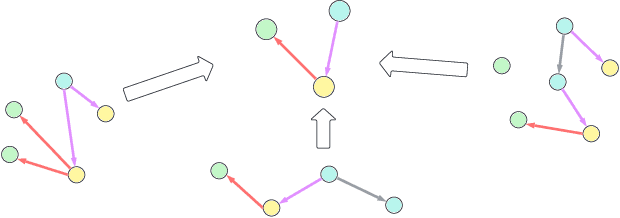
Causal representation learning (CRL) enhances machine learning models' robustness and generalizability by learning structural causal models associated with data-generating processes. We focus on a family of CRL methods that uses contrastive data pairs in the observable space, generated before and after a random, unknown intervention, to identify the latent causal model. (Brehmer et al., 2022) showed that this is indeed possible, given that all latent variables can be intervened on individually. However, this is a highly restrictive assumption in many systems. In this work, we instead assume interventions on arbitrary subsets of latent variables, which is more realistic. We introduce a theoretical framework that calculates the degree to which we can identify a causal model, given a set of possible interventions, up to an abstraction that describes the system at a higher level of granularity.

SymmCD: Symmetry-Preserving Crystal Generation with Diffusion Models

Generating novel crystalline materials has potential to lead to advancements in fields such as electronics, energy storage, and catalysis. The defining characteristic of crystals is their symmetry, which plays a central role in determining their physical properties. However, existing crystal generation methods either fail to generate materials that display the symmetries of real-world crystals, or simply replicate the symmetry information from examples in a database. To address this limitation, we propose SymmCD, a novel diffusion-based generative model that explicitly incorporates crystallographic symmetry into the generative process. We decompose crystals into two components and learn their joint distribution through diffusion: 1) the asymmetric unit, the smallest subset of the crystal which can generate the whole crystal through symmetry transformations, and; 2) the symmetry transformations needed to be applied to each atom in the asymmetric unit. We also use a novel and interpretable representation for these transformations, enabling generalization across different crystallographic symmetry groups. We showcase the competitive performance of SymmCD on a subset of the Materials Project, obtaining diverse and valid crystals with realistic symmetries and predicted properties.

Symmetry-Aware Generative Modeling through Learned Canonicalization

Generative modeling of symmetric densities has a range of applications in AI for science, from drug discovery to physics simulations. The existing generative modeling paradigm for invariant densities combines an invariant prior with an equivariant generative process. However, we observe that this technique is not necessary and has several drawbacks resulting from the limitations of equivariant networks. Instead, we propose to model a learned slice of the density so that only one representative element per orbit is learned. To accomplish this, we learn a group-equivariant canonicalization network that maps training samples to a canonical pose and train a non-equivariant generative model over these canonicalized samples. We implement this idea in the context of diffusion models. Our preliminary experimental results on molecular modeling are promising, demonstrating improved sample quality and faster inference time.

Symmetry Breaking and Equivariant Neural Networks

Using symmetry as an inductive bias in deep learning has been proven to be a principled approach for sample-efficient model design. However, the relationship between symmetry and the imperative for equivariance in neural networks is not always obvious. Here, we analyze a key limitation that arises in equivariant functions: their incapacity to break symmetry at the level of individual data samples. In response, we introduce a novel notion of 'relaxed equivariance' that circumvents this limitation. We further demonstrate how to incorporate this relaxation into equivariant multilayer perceptrons (E-MLPs), offering an alternative to the noise-injection method. The relevance of symmetry breaking is then discussed in various application domains: physics, graph representation learning, combinatorial optimization and equivariant decoding.

Equivariant Adaptation of Large Pre-Trained Models

Equivariant networks are specifically designed to ensure consistent behavior with respect to a set of input transformations, leading to higher sample efficiency and more accurate and robust predictions. However, redesigning each component of prevalent deep neural network architectures to achieve chosen equivariance is a difficult problem and can result in a computationally expensive network during both training and inference. A recently proposed alternative towards equivariance that removes the architectural constraints is to use a simple canonicalization network that transforms the input to a canonical form before feeding it to an unconstrained prediction network. We show here that this approach can effectively be used to make a large pre-trained network equivariant. However, we observe that the produced canonical orientations can be misaligned with those of the training distribution, hindering performance. Using dataset-dependent priors to inform the canonicalization function, we are able to make large pre-trained models equivariant while maintaining their performance. This significantly improves the robustness of these models to deterministic transformations of the data, such as rotations. We believe this equivariant adaptation of large pre-trained models can help their domain-specific applications with known symmetry priors.

Using Multiple Vector Channels Improves E(n)-Equivariant Graph Neural Networks

We present a natural extension to E(n)-equivariant graph neural networks that uses multiple equivariant vectors per node. We formulate the extension and show that it improves performance across different physical systems benchmark tasks, with minimal differences in runtime or number of parameters. The proposed multichannel EGNN outperforms the standard singlechannel EGNN on N-body charged particle dynamics, molecular property predictions, and predicting the trajectories of solar system bodies. Given the additional benefits and minimal additional cost of multi-channel EGNN, we suggest that this extension may be of practical use to researchers working in machine learning for the physical sciences

Equivariant Networks for Crystal Structures

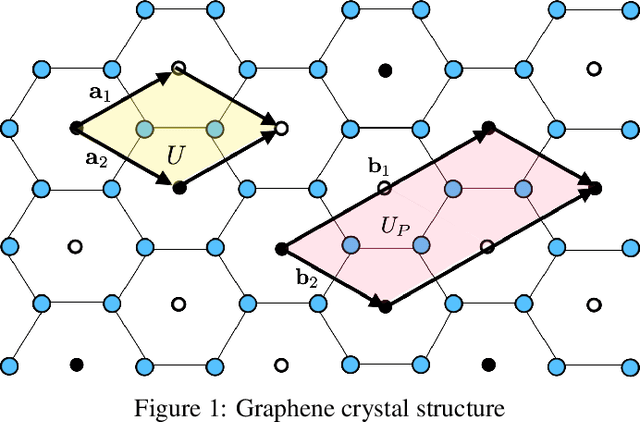
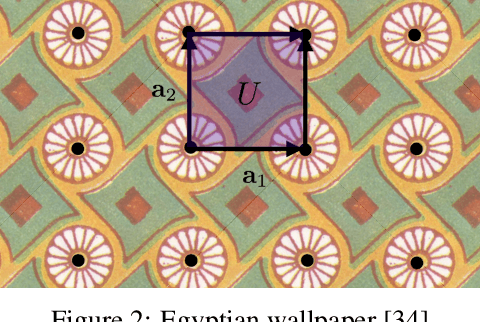
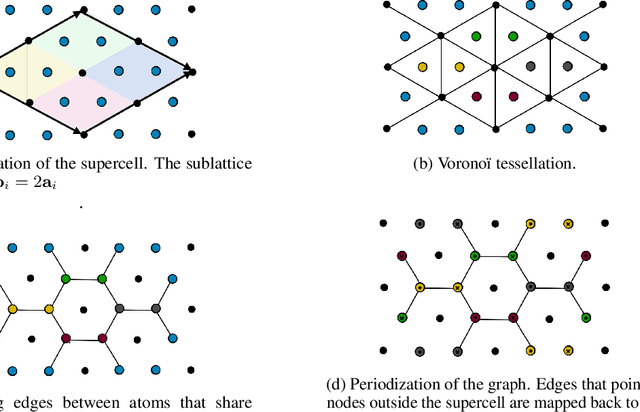
Supervised learning with deep models has tremendous potential for applications in materials science. Recently, graph neural networks have been used in this context, drawing direct inspiration from models for molecules. However, materials are typically much more structured than molecules, which is a feature that these models do not leverage. In this work, we introduce a class of models that are equivariant with respect to crystalline symmetry groups. We do this by defining a generalization of the message passing operations that can be used with more general permutation groups, or that can alternatively be seen as defining an expressive convolution operation on the crystal graph. Empirically, these models achieve competitive results with state-of-the-art on property prediction tasks.

Equivariance with Learned Canonicalization Functions

Symmetry-based neural networks often constrain the architecture in order to achieve invariance or equivariance to a group of transformations. In this paper, we propose an alternative that avoids this architectural constraint by learning to produce a canonical representation of the data. These canonicalization functions can readily be plugged into non-equivariant backbone architectures. We offer explicit ways to implement them for many groups of interest. We show that this approach enjoys universality while providing interpretable insights. Our main hypothesis is that learning a neural network to perform canonicalization is better than using predefined heuristics. Our results show that learning the canonicalization function indeed leads to better results and that the approach achieves excellent performance in practice.

Prediction of Large Magnetic Moment Materials With Graph Neural Networks and Random Forests

Magnetic materials are crucial components of many technologies that could drive the ecological transition, including electric motors, wind turbine generators and magnetic refrigeration systems. Discovering materials with large magnetic moments is therefore an increasing priority. Here, using state-of-the-art machine learning methods, we scan the Inorganic Crystal Structure Database (ICSD) of hundreds of thousands of existing materials to find those that are ferromagnetic and have large magnetic moments. Crystal graph convolutional neural networks (CGCNN), materials graph network (MEGNet) and random forests are trained on the Materials Project database that contains the results of high-throughput DFT predictions. For random forests, we use a stochastic method to select nearly one hundred relevant descriptors based on chemical composition and crystal structure. This turns out to give results for the test sets that are comparable to those of neural networks. The comparison between these different machine learning approaches gives an estimate of the errors for our predictions on the ICSD database.