Equivariant Networks for Crystal Structures
Paper and Code
Nov 15, 2022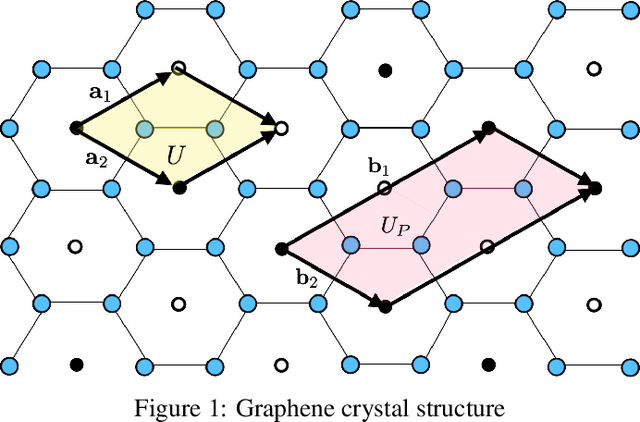

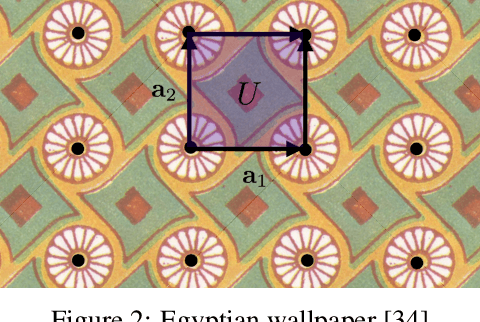
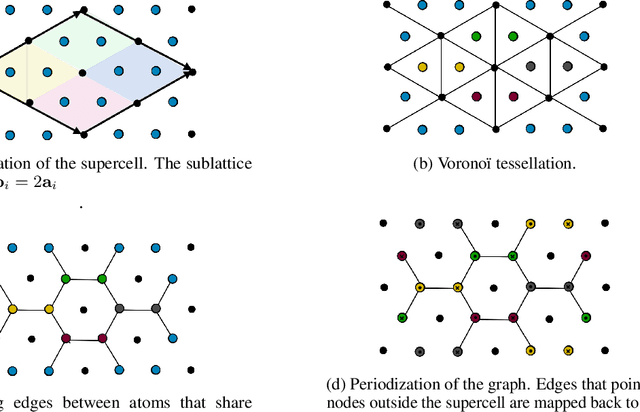
Supervised learning with deep models has tremendous potential for applications in materials science. Recently, graph neural networks have been used in this context, drawing direct inspiration from models for molecules. However, materials are typically much more structured than molecules, which is a feature that these models do not leverage. In this work, we introduce a class of models that are equivariant with respect to crystalline symmetry groups. We do this by defining a generalization of the message passing operations that can be used with more general permutation groups, or that can alternatively be seen as defining an expressive convolution operation on the crystal graph. Empirically, these models achieve competitive results with state-of-the-art on property prediction tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge