Disciplined Geodesically Convex Programming

Convex programming plays a fundamental role in machine learning, data science, and engineering. Testing convexity structure in nonlinear programs relies on verifying the convexity of objectives and constraints. \citet{grant2006disciplined} introduced a framework, Disciplined Convex Programming (DCP), for automating this verification task for a wide range of convex functions that can be decomposed into basic convex functions (atoms) using convexity-preserving compositions and transformations (rules). However, the restriction to Euclidean convexity concepts can limit the applicability of the framework. For instance, many notable instances of statistical estimators and matrix-valued (sub)routines in machine learning applications are Euclidean non-convex, but exhibit geodesic convexity through a more general Riemannian lens. In this work, we extend disciplined programming to this setting by introducing Disciplined Geodesically Convex Programming (DGCP). We determine convexity-preserving compositions and transformations for geodesically convex functions on general Cartan-Hadamard manifolds, as well as for the special case of symmetric positive definite matrices, a common setting in matrix-valued optimization. For the latter, we also define a basic set of atoms. Our paper is accompanied by a Julia package SymbolicAnalysis.jl, which provides functionality for testing and certifying DGCP-compliant expressions. Our library interfaces with manifold optimization software, which allows for directly solving verified geodesically convex programs.

Bayesian Neural Ordinary Differential Equations

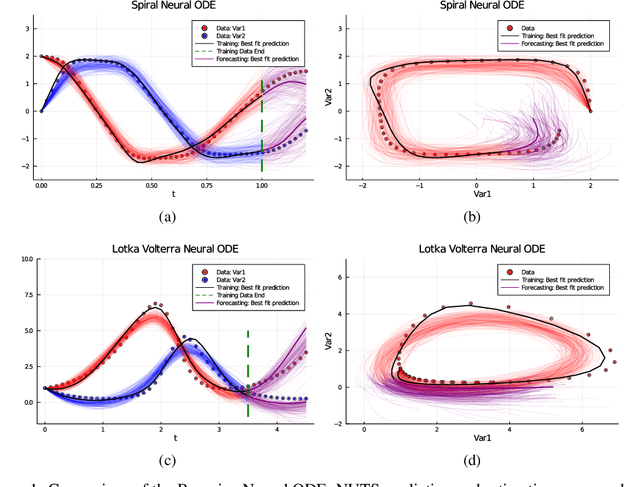
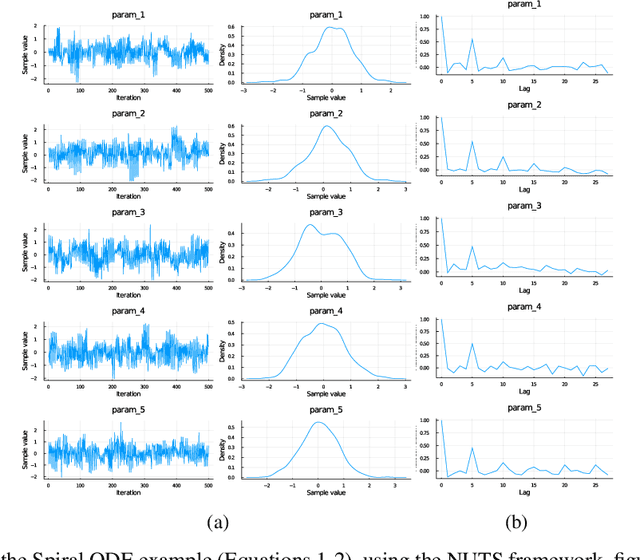
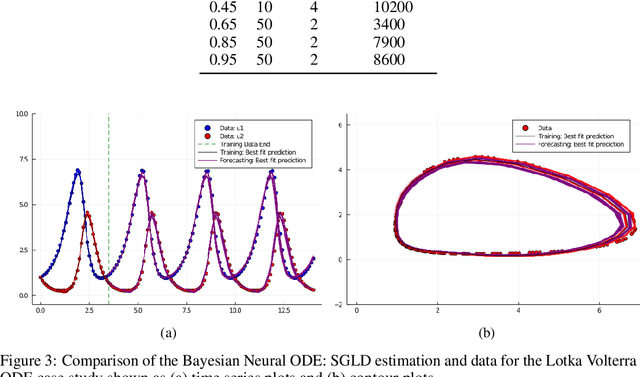
Recently, Neural Ordinary Differential Equations has emerged as a powerful framework for modeling physical simulations without explicitly defining the ODEs governing the system, but learning them via machine learning. However, the question: Can Bayesian learning frameworks be integrated with Neural ODEs to robustly quantify the uncertainty in the weights of a Neural ODE? remains unanswered. In an effort to address this question, we demonstrate the successful integration of Neural ODEs with two methods of Bayesian Inference: (a) The No-U-Turn MCMC sampler (NUTS) and (b) Stochastic Langevin Gradient Descent (SGLD). We test the performance of our Bayesian Neural ODE approach on classical physical systems, as well as on standard machine learning datasets like MNIST, using GPU acceleration. Finally, considering a simple example, we demonstrate the probabilistic identification of model specification in partially-described dynamical systems using universal ordinary differential equations. Together, this gives a scientific machine learning tool for probabilistic estimation of epistemic uncertainties.

DiffEqFlux.jl - A Julia Library for Neural Differential Equations

DiffEqFlux.jl is a library for fusing neural networks and differential equations. In this work we describe differential equations from the viewpoint of data science and discuss the complementary nature between machine learning models and differential equations. We demonstrate the ability to incorporate DifferentialEquations.jl-defined differential equation problems into a Flux-defined neural network, and vice versa. The advantages of being able to use the entire DifferentialEquations.jl suite for this purpose is demonstrated by counter examples where simple integration strategies fail, but the sophisticated integration strategies provided by the DifferentialEquations.jl library succeed. This is followed by a demonstration of delay differential equations and stochastic differential equations inside of neural networks. We show high-level functionality for defining neural ordinary differential equations (neural networks embedded into the differential equation) and describe the extra models in the Flux model zoo which includes neural stochastic differential equations. We conclude by discussing the various adjoint methods used for backpropogation of the differential equation solvers. DiffEqFlux.jl is an important contribution to the area, as it allows the full weight of the differential equation solvers developed from decades of research in the scientific computing field to be readily applied to the challenges posed by machine learning and data science.