Symplectic Neural Flows for Modeling and Discovery

Hamilton's equations are fundamental for modeling complex physical systems, where preserving key properties such as energy and momentum is crucial for reliable long-term simulations. Geometric integrators are widely used for this purpose, but neural network-based methods that incorporate these principles remain underexplored. This work introduces SympFlow, a time-dependent symplectic neural network designed using parameterized Hamiltonian flow maps. This design allows for backward error analysis and ensures the preservation of the symplectic structure. SympFlow allows for two key applications: (i) providing a time-continuous symplectic approximation of the exact flow of a Hamiltonian system--purely based on the differential equations it satisfies, and (ii) approximating the flow map of an unknown Hamiltonian system relying on trajectory data. We demonstrate the effectiveness of SympFlow on diverse problems, including chaotic and dissipative systems, showing improved energy conservation compared to general-purpose numerical methods and accurate

Benchmarking learned algorithms for computed tomography image reconstruction tasks

Computed tomography (CT) is a widely used non-invasive diagnostic method in various fields, and recent advances in deep learning have led to significant progress in CT image reconstruction. However, the lack of large-scale, open-access datasets has hindered the comparison of different types of learned methods. To address this gap, we use the 2DeteCT dataset, a real-world experimental computed tomography dataset, for benchmarking machine learning based CT image reconstruction algorithms. We categorize these methods into post-processing networks, learned/unrolled iterative methods, learned regularizer methods, and plug-and-play methods, and provide a pipeline for easy implementation and evaluation. Using key performance metrics, including SSIM and PSNR, our benchmarking results showcase the effectiveness of various algorithms on tasks such as full data reconstruction, limited-angle reconstruction, sparse-angle reconstruction, low-dose reconstruction, and beam-hardening corrected reconstruction. With this benchmarking study, we provide an evaluation of a range of algorithms representative for different categories of learned reconstruction methods on a recently published dataset of real-world experimental CT measurements. The reproducible setup of methods and CT image reconstruction tasks in an open-source toolbox enables straightforward addition and comparison of new methods later on. The toolbox also provides the option to load the 2DeteCT dataset differently for extensions to other problems and different CT reconstruction tasks.

Hamiltonian Matching for Symplectic Neural Integrators

Hamilton's equations of motion form a fundamental framework in various branches of physics, including astronomy, quantum mechanics, particle physics, and climate science. Classical numerical solvers are typically employed to compute the time evolution of these systems. However, when the system spans multiple spatial and temporal scales numerical errors can accumulate, leading to reduced accuracy. To address the challenges of evolving such systems over long timescales, we propose SympFlow, a novel neural network-based symplectic integrator, which is the composition of a sequence of exact flow maps of parametrised time-dependent Hamiltonian functions. This architecture allows for a backward error analysis: we can identify an underlying Hamiltonian function of the architecture and use it to define a Hamiltonian matching objective function, which we use for training. In numerical experiments, we show that SympFlow exhibits promising results, with qualitative energy conservation behaviour similar to that of time-stepping symplectic integrators.

Lie Algebra Canonicalization: Equivariant Neural Operators under arbitrary Lie Groups

The quest for robust and generalizable machine learning models has driven recent interest in exploiting symmetries through equivariant neural networks. In the context of PDE solvers, recent works have shown that Lie point symmetries can be a useful inductive bias for Physics-Informed Neural Networks (PINNs) through data and loss augmentation. Despite this, directly enforcing equivariance within the model architecture for these problems remains elusive. This is because many PDEs admit non-compact symmetry groups, oftentimes not studied beyond their infinitesimal generators, making them incompatible with most existing equivariant architectures. In this work, we propose Lie aLgebrA Canonicalization (LieLAC), a novel approach that exploits only the action of infinitesimal generators of the symmetry group, circumventing the need for knowledge of the full group structure. To achieve this, we address existing theoretical issues in the canonicalization literature, establishing connections with frame averaging in the case of continuous non-compact groups. Operating within the framework of canonicalization, LieLAC can easily be integrated with unconstrained pre-trained models, transforming inputs to a canonical form before feeding them into the existing model, effectively aligning the input for model inference according to allowed symmetries. LieLAC utilizes standard Lie group descent schemes, achieving equivariance in pre-trained models. Finally, we showcase LieLAC's efficacy on tasks of invariant image classification and Lie point symmetry equivariant neural PDE solvers using pre-trained models.

Contractive Systems Improve Graph Neural Networks Against Adversarial Attacks

Graph Neural Networks (GNNs) have established themselves as a key component in addressing diverse graph-based tasks. Despite their notable successes, GNNs remain susceptible to input perturbations in the form of adversarial attacks. This paper introduces an innovative approach to fortify GNNs against adversarial perturbations through the lens of contractive dynamical systems. Our method introduces graph neural layers based on differential equations with contractive properties, which, as we show, improve the robustness of GNNs. A distinctive feature of the proposed approach is the simultaneous learned evolution of both the node features and the adjacency matrix, yielding an intrinsic enhancement of model robustness to perturbations in the input features and the connectivity of the graph. We mathematically derive the underpinnings of our novel architecture and provide theoretical insights to reason about its expected behavior. We demonstrate the efficacy of our method through numerous real-world benchmarks, reading on par or improved performance compared to existing methods.

Convergent regularization in inverse problems and linear plug-and-play denoisers

Plug-and-play (PnP) denoising is a popular iterative framework for solving imaging inverse problems using off-the-shelf image denoisers. Their empirical success has motivated a line of research that seeks to understand the convergence of PnP iterates under various assumptions on the denoiser. While a significant amount of research has gone into establishing the convergence of the PnP iteration for different regularity conditions on the denoisers, not much is known about the asymptotic properties of the converged solution as the noise level in the measurement tends to zero, i.e., whether PnP methods are provably convergent regularization schemes under reasonable assumptions on the denoiser. This paper serves two purposes: first, we provide an overview of the classical regularization theory in inverse problems and survey a few notable recent data-driven methods that are provably convergent regularization schemes. We then continue to discuss PnP algorithms and their established convergence guarantees. Subsequently, we consider PnP algorithms with linear denoisers and propose a novel spectral filtering technique to control the strength of regularization arising from the denoiser. Further, by relating the implicit regularization of the denoiser to an explicit regularization functional, we rigorously show that PnP with linear denoisers leads to a convergent regularization scheme. More specifically, we prove that in the limit as the noise vanishes, the PnP reconstruction converges to the minimizer of a regularization potential subject to the solution satisfying the noiseless operator equation. The theoretical analysis is corroborated by numerical experiments for the classical inverse problem of tomographic image reconstruction.

Designing Stable Neural Networks using Convex Analysis and ODEs

Motivated by classical work on the numerical integration of ordinary differential equations we present a ResNet-styled neural network architecture that encodes non-expansive (1-Lipschitz) operators, as long as the spectral norms of the weights are appropriately constrained. This is to be contrasted with the ordinary ResNet architecture which, even if the spectral norms of the weights are constrained, has a Lipschitz constant that, in the worst case, grows exponentially with the depth of the network. Further analysis of the proposed architecture shows that the spectral norms of the weights can be further constrained to ensure that the network is an averaged operator, making it a natural candidate for a learned denoiser in Plug-and-Play algorithms. Using a novel adaptive way of enforcing the spectral norm constraints, we show that, even with these constraints, it is possible to train performant networks. The proposed architecture is applied to the problem of adversarially robust image classification, to image denoising, and finally to the inverse problem of deblurring.

Dynamical systems' based neural networks

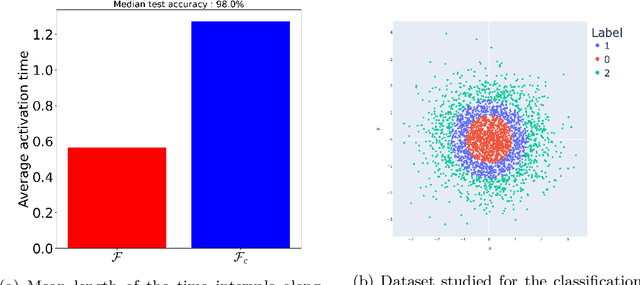
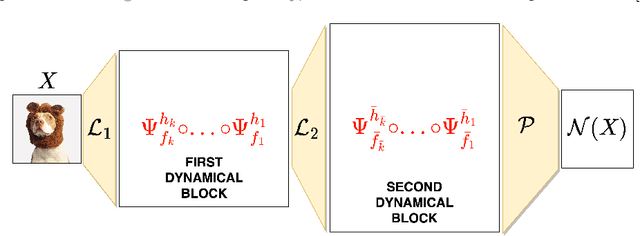
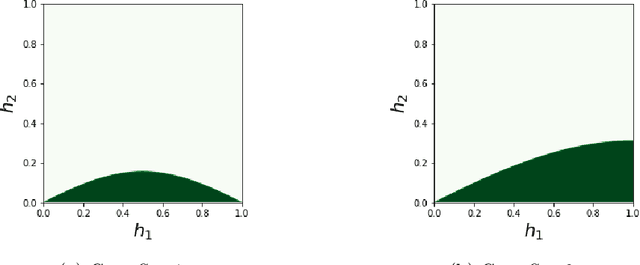
Neural networks have gained much interest because of their effectiveness in many applications. However, their mathematical properties are generally not well understood. If there is some underlying geometric structure inherent to the data or to the function to approximate, it is often desirable to take this into account in the design of the neural network. In this work, we start with a non-autonomous ODE and build neural networks using a suitable, structure-preserving, numerical time-discretisation. The structure of the neural network is then inferred from the properties of the ODE vector field. Besides injecting more structure into the network architectures, this modelling procedure allows a better theoretical understanding of their behaviour. We present two universal approximation results and demonstrate how to impose some particular properties on the neural networks. A particular focus is on 1-Lipschitz architectures including layers that are not 1-Lipschitz. These networks are expressive and robust against adversarial attacks, as shown for the CIFAR-10 dataset.

Imaging with Equivariant Deep Learning

From early image processing to modern computational imaging, successful models and algorithms have relied on a fundamental property of natural signals: symmetry. Here symmetry refers to the invariance property of signal sets to transformations such as translation, rotation or scaling. Symmetry can also be incorporated into deep neural networks in the form of equivariance, allowing for more data-efficient learning. While there has been important advances in the design of end-to-end equivariant networks for image classification in recent years, computational imaging introduces unique challenges for equivariant network solutions since we typically only observe the image through some noisy ill-conditioned forward operator that itself may not be equivariant. We review the emerging field of equivariant imaging and show how it can provide improved generalization and new imaging opportunities. Along the way we show the interplay between the acquisition physics and group actions and links to iterative reconstruction, blind compressed sensing and self-supervised learning.

Equivariant neural networks for inverse problems

In recent years the use of convolutional layers to encode an inductive bias (translational equivariance) in neural networks has proven to be a very fruitful idea. The successes of this approach have motivated a line of research into incorporating other symmetries into deep learning methods, in the form of group equivariant convolutional neural networks. Much of this work has been focused on roto-translational symmetry of $\mathbf R^d$, but other examples are the scaling symmetry of $\mathbf R^d$ and rotational symmetry of the sphere. In this work, we demonstrate that group equivariant convolutional operations can naturally be incorporated into learned reconstruction methods for inverse problems that are motivated by the variational regularisation approach. Indeed, if the regularisation functional is invariant under a group symmetry, the corresponding proximal operator will satisfy an equivariance property with respect to the same group symmetry. As a result of this observation, we design learned iterative methods in which the proximal operators are modelled as group equivariant convolutional neural networks. We use roto-translationally equivariant operations in the proposed methodology and apply it to the problems of low-dose computerised tomography reconstruction and subsampled magnetic resonance imaging reconstruction. The proposed methodology is demonstrated to improve the reconstruction quality of a learned reconstruction method with a little extra computational cost at training time but without any extra cost at test time.