CBCT-IQ: A Publicly Available Annotated Cone-Beam CT Dataset for Image Quality Assessment and Benchmarking

Medical image quality plays a critical role in diagnostic accuracy, especially in X-ray-based imaging modalities such as cone-beam computed tomography (CBCT), where image quality must be balanced against radiation dose. While expert visual evaluation remains the clinical standard for image quality evaluation, it is time-consuming, subjective and affected by inter-observer variability, emphasizing the need for reliable quantitative image quality assessment (IQA) methods. However, the development and validation of such IQA methods have been limited by the lack of publicly available CBCT datasets with expert image quality annotations. In this study, we provide the first open-access CBCT IQA dataset containing 1,764 annotated image slices acquired using systematic variations in image acquisition and reconstruction parameters. Three clinical experts graded the overall image quality and a predefined regions of interest (ROI) using a four-level scoring scheme. In addition, we benchmark 26 full reference- and no reference-based IQA measures against expert annotations and introduce an exploratory IQA measure-based ranking capable of distinguishing subtle image quality differences. This dataset introduced a standardized benchmark for future CBCT IQA research and provides a valuable resource for the development and validation of new IQA methods, enabling reproducible research and advancing CBCT IQA.

DeepCormack: Fermi surface tomography using model-based data-driven algorithms

The experimental reconstruction of the 3D two-photon momentum density (TPMD) via angular correlation of electron-positron annihilation radiation (ACAR) is a particularly useful method for studying material Fermi surfaces. It does not rely on low temperatures, UHV conditions, or strong magnetic fields, and enables the study of the spin-resolved electronic structure of materials. Yet, it remains a challenging inverse problem. Typically, 10^8 positron annihilation events are measured for 3--6 projections of the TPMD at different angles. The standard reconstruction approach is an ACAR adaptation of Cormack's method (the MCM) that leverages the inherent symmetry in the crystal's structure. However, the poor signal-to-noise ratio means collecting data of sufficient quality for Fermi surface studies can take months per sample. We present DeepCormack, a family of data-driven model-based reconstruction algorithms that augments the MCM by integrating supervised deep-learning models (CNN, MLP, and UNet) at various stages. To overcome the lack of large experimental training sets, we propose a method which leverages singular value decomposition with dynamic mode decomposition to generate realistic synthetic TPMD volumes, requiring only a single reference momentum density computed via density functional theory. On test data, DeepCormack improves reconstruction quality over MCM by about 8.5 dB PSNR at 200M counts and remains stable at reduced counts, enabling significantly faster acquisition times. Generalisation to experimental data depends strongly on how well the training distribution from the reference momentum density matches the sample. We therefore recommend pairing DeepCormack with a DFT calculation of the target material to create sample-specific training data. Our proposed method offers either much higher quality reconstructions, or enables significantly faster ones, on the order of weeks.

Design Choices in Splitting-Based Self-Supervised Sparse-View CT Reconstruction

Self-supervised data splitting has emerged as a promising paradigm for sparse-view CT reconstruction, enabling training from incomplete measurements without fully sampled ground truth. However, the influence of key design choices, including partitioning strategy, preprocessing, and inference, remains insufficiently understood. In this work, we introduce a unified framework that decomposes splitting-based reconstruction into these three components, enabling controlled comparison of existing methods and two incremental extensions: multi-partition splitting and an alternative inference strategy. Experiments on simulated LoDoPaB-CT data under independent and correlated noise, together with validation on the real-world 2DeteCT dataset, show that the optimal partitioning strategy strongly depends on the measurement noise structure. Lattice-based splitting performs favorably under independent noise, whereas angular masking is more robust under correlated noise and real measured data. Multi-partition splitting consistently improves over pure projection-wise splitting in several settings. Complementary perceptual and structural metrics, including LPIPS and HaarPSI, reveal differences between masking strategies that are less apparent from PSNR and SSIM alone. These results provide practical guidelines for designing self-supervised sparse-view CT reconstruction methods and highlight the limitations of common independence assumptions in realistic imaging environments.

No-reference based automatic parameter optimization for iterative reconstruction using a novel search space aware crow search algorithm

Iterative reconstruction technique's ability to reduce radiation exposure by using fewer projections has attracted significant attention. However, these methods typically require a precise tuning of several hyperparameters, which can have a major impact on reconstruction quality. Manually setting these parameters is time-consuming and increases the workload for human operators. In this paper, we introduce a novel fully automatic parameter optimization framework that can be applied to a wide range of Cone-beam computed tomography (CBCT) iterative reconstruction algorithms to determine optimal parameters without requiring a reference reconstruction. The proposed method incorporates a modified crow search algorithm (CSA) featuring a superior set-dependent local search mechanism, a search-space-aware global search strategy, and an objective-driven balance between local and global search. Additionally, to ensure an effective initial population, we propose a chaotic diagonal linear uniform initialization scheme that accelerates algorithm convergence. The performance of the proposed framework was evaluated on three imaging machines and four real datasets, as well as three different iterative reconstruction methods with the highest number of tunable parameters, representing the most challenging senario. The results indicate that the proposed method could outperform manual settings and CSA, with an 4.19% improvement in average fitness and 4.89% and 3.82% improvements on CHILL@UK and RPI_AXIS, respectively, which are two benchmark no-reference learning-based quality metrics. In addition, the qualitative results clearly show the superiority of the proposed method by maintaining fine details sharply. The overall performance of the proposed framework across different comparison scenarios demonstrates its effectiveness and robustness across all cases.

LamiGauss: Pitching Radiative Gaussian for Sparse-View X-ray Laminography Reconstruction

X-ray Computed Laminography (CL) is essential for non-destructive inspection of plate-like structures in applications such as microchips and composite battery materials, where traditional computed tomography (CT) struggles due to geometric constraints. However, reconstructing high-quality volumes from laminographic projections remains challenging, particularly under highly sparse-view acquisition conditions. In this paper, we propose a reconstruction algorithm, namely LamiGauss, that combines Gaussian Splatting radiative rasterization with a dedicated detector-to-world transformation model incorporating the laminographic tilt angle. LamiGauss leverages an initialization strategy that explicitly filters out common laminographic artifacts from the preliminary reconstruction, preventing redundant Gaussians from being allocated to false structures and thereby concentrating model capacity on representing the genuine object. Our approach effectively optimizes directly from sparse projections, enabling accurate and efficient reconstruction with limited data. Extensive experiments on both synthetic and real datasets demonstrate the effectiveness and superiority of the proposed method over existing techniques. LamiGauss uses only 3$\%$ of full views to achieve superior performance over the iterative method optimized on a full dataset.

Smooth Model Compression without Fine-Tuning

Compressing and pruning large machine learning models has become a critical step towards their deployment in real-world applications. Standard pruning and compression techniques are typically designed without taking the structure of the network's weights into account, limiting their effectiveness. We explore the impact of smooth regularization on neural network training and model compression. By applying nuclear norm, first- and second-order derivative penalties of the weights during training, we encourage structured smoothness while preserving predictive performance on par with non-smooth models. We find that standard pruning methods often perform better when applied to these smooth models. Building on this observation, we apply a Singular-Value-Decomposition-based compression method that exploits the underlying smooth structure and approximates the model's weight tensors by smaller low-rank tensors. Our approach enables state-of-the-art compression without any fine-tuning - reaching up to $91\%$ accuracy on a smooth ResNet-18 on CIFAR-10 with $70\%$ fewer parameters.

Noisier2Inverse: Self-Supervised Learning for Image Reconstruction with Correlated Noise

We propose Noisier2Inverse, a correction-free self-supervised deep learning approach for general inverse prob- lems. The proposed method learns a reconstruction function without the need for ground truth samples and is ap- plicable in cases where measurement noise is statistically correlated. This includes computed tomography, where detector imperfections or photon scattering create correlated noise patterns, as well as microscopy and seismic imaging, where physical interactions during measurement introduce dependencies in the noise structure. Similar to Noisier2Noise, a key step in our approach is the generation of noisier data from which the reconstruction net- work learns. However, unlike Noisier2Noise, the proposed loss function operates in measurement space and is trained to recover an extrapolated image instead of the original noisy one. This eliminates the need for an extrap- olation step during inference, which would otherwise suffer from ill-posedness. We numerically demonstrate that our method clearly outperforms previous self-supervised approaches that account for correlated noise.

Benchmarking learned algorithms for computed tomography image reconstruction tasks

Computed tomography (CT) is a widely used non-invasive diagnostic method in various fields, and recent advances in deep learning have led to significant progress in CT image reconstruction. However, the lack of large-scale, open-access datasets has hindered the comparison of different types of learned methods. To address this gap, we use the 2DeteCT dataset, a real-world experimental computed tomography dataset, for benchmarking machine learning based CT image reconstruction algorithms. We categorize these methods into post-processing networks, learned/unrolled iterative methods, learned regularizer methods, and plug-and-play methods, and provide a pipeline for easy implementation and evaluation. Using key performance metrics, including SSIM and PSNR, our benchmarking results showcase the effectiveness of various algorithms on tasks such as full data reconstruction, limited-angle reconstruction, sparse-angle reconstruction, low-dose reconstruction, and beam-hardening corrected reconstruction. With this benchmarking study, we provide an evaluation of a range of algorithms representative for different categories of learned reconstruction methods on a recently published dataset of real-world experimental CT measurements. The reproducible setup of methods and CT image reconstruction tasks in an open-source toolbox enables straightforward addition and comparison of new methods later on. The toolbox also provides the option to load the 2DeteCT dataset differently for extensions to other problems and different CT reconstruction tasks.

Learned denoising with simulated and experimental low-dose CT data

Like in many other research fields, recent developments in computational imaging have focused on developing machine learning (ML) approaches to tackle its main challenges. To improve the performance of computational imaging algorithms, machine learning methods are used for image processing tasks such as noise reduction. Generally, these ML methods heavily rely on the availability of high-quality data on which they are trained. This work explores the application of ML methods, specifically convolutional neural networks (CNNs), in the context of noise reduction for computed tomography (CT) imaging. We utilize a large 2D computed tomography dataset for machine learning to carry out for the first time a comprehensive study on the differences between the observed performances of algorithms trained on simulated noisy data and on real-world experimental noisy data. The study compares the performance of two common CNN architectures, U-Net and MSD-Net, that are trained and evaluated on both simulated and experimental noisy data. The results show that while sinogram denoising performed better with simulated noisy data if evaluated in the sinogram domain, the performance did not carry over to the reconstruction domain where training on experimental noisy data shows a higher performance in denoising experimental noisy data. Training the algorithms in an end-to-end fashion from sinogram to reconstruction significantly improved model performance, emphasizing the importance of matching raw measurement data to high-quality CT reconstructions. The study furthermore suggests the need for more sophisticated noise simulation approaches to bridge the gap between simulated and real-world data in CT image denoising applications and gives insights into the challenges and opportunities in leveraging simulated data for machine learning in computational imaging.

A study of why we need to reassess full reference image quality assessment with medical images

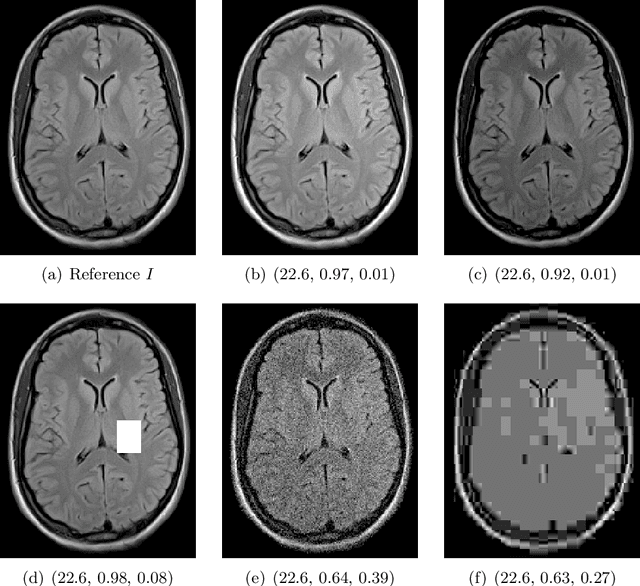
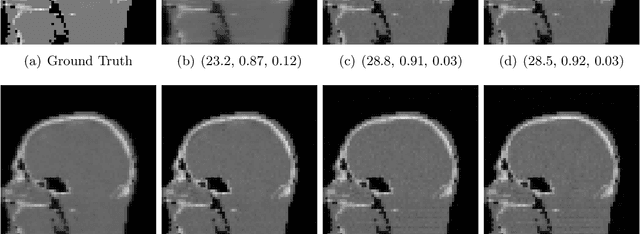
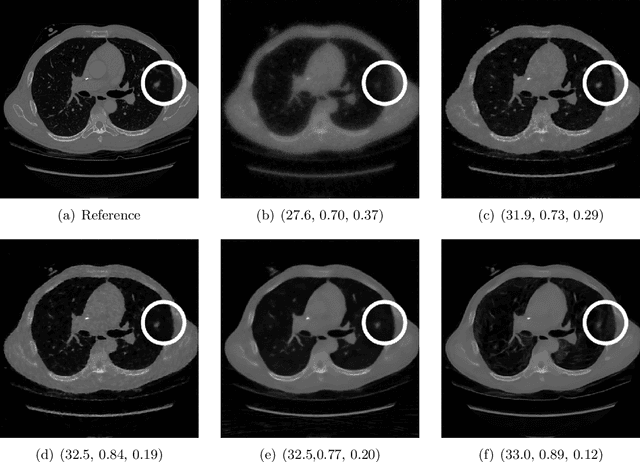
Image quality assessment (IQA) is not just indispensable in clinical practice to ensure high standards, but also in the development stage of novel algorithms that operate on medical images with reference data. This paper provides a structured and comprehensive collection of examples where the two most common full reference (FR) image quality measures prove to be unsuitable for the assessment of novel algorithms using different kinds of medical images, including real-world MRI, CT, OCT, X-Ray, digital pathology and photoacoustic imaging data. In particular, the FR-IQA measures PSNR and SSIM are known and tested for working successfully in many natural imaging tasks, but discrepancies in medical scenarios have been noted in the literature. Inconsistencies arising in medical images are not surprising, as they have very different properties than natural images which have not been targeted nor tested in the development of the mentioned measures, and therefore might imply wrong judgement of novel methods for medical images. Therefore, improvement is urgently needed in particular in this era of AI to increase explainability, reproducibility and generalizability in machine learning for medical imaging and beyond. On top of the pitfalls we will provide ideas for future research as well as suggesting guidelines for the usage of FR-IQA measures applied to medical images.