Enhancing the Utility of Higher-Order Information in Relational Learning

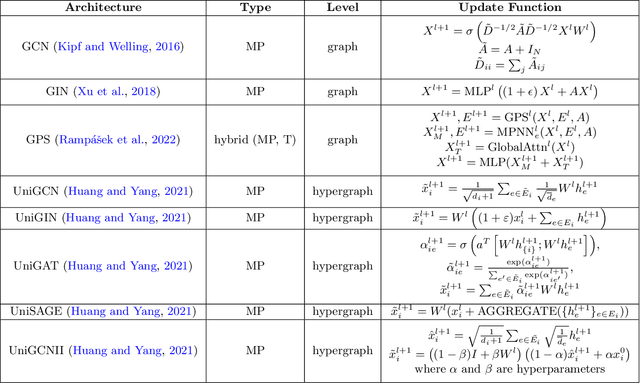
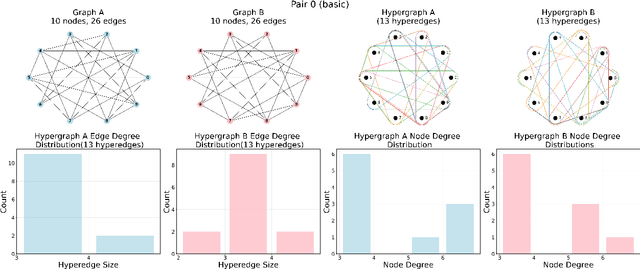
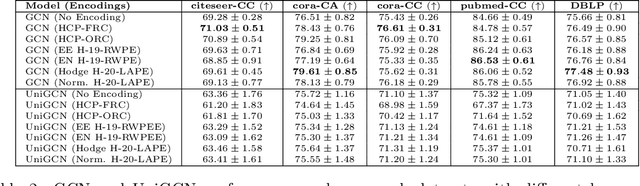
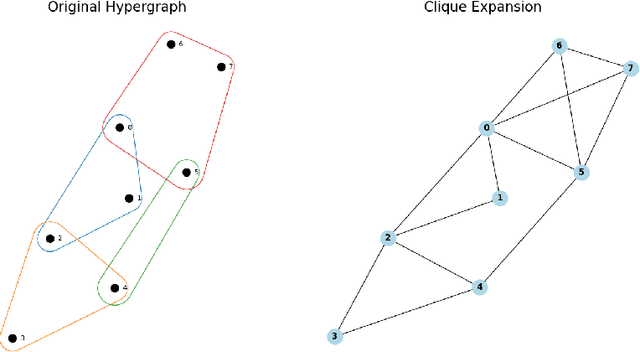
Higher-order information is crucial for relational learning in many domains where relationships extend beyond pairwise interactions. Hypergraphs provide a natural framework for modeling such relationships, which has motivated recent extensions of graph neural net- work architectures to hypergraphs. However, comparisons between hypergraph architectures and standard graph-level models remain limited. In this work, we systematically evaluate a selection of hypergraph-level and graph-level architectures, to determine their effectiveness in leveraging higher-order information in relational learning. Our results show that graph-level architectures applied to hypergraph expansions often outperform hypergraph- level ones, even on inputs that are naturally parametrized as hypergraphs. As an alternative approach for leveraging higher-order information, we propose hypergraph-level encodings based on classical hypergraph characteristics. While these encodings do not significantly improve hypergraph architectures, they yield substantial performance gains when combined with graph-level models. Our theoretical analysis shows that hypergraph-level encodings provably increase the representational power of message-passing graph neural networks beyond that of their graph-level counterparts.

Multimodal Medical Code Tokenizer

Foundation models trained on patient electronic health records (EHRs) require tokenizing medical data into sequences of discrete vocabulary items. Existing tokenizers treat medical codes from EHRs as isolated textual tokens. However, each medical code is defined by its textual description, its position in ontological hierarchies, and its relationships to other codes, such as disease co-occurrences and drug-treatment associations. Medical vocabularies contain more than 600,000 codes with critical information for clinical reasoning. We introduce MedTok, a multimodal medical code tokenizer that uses the text descriptions and relational context of codes. MedTok processes text using a language model encoder and encodes the relational structure with a graph encoder. It then quantizes both modalities into a unified token space, preserving modality-specific and cross-modality information. We integrate MedTok into five EHR models and evaluate it on operational and clinical tasks across in-patient and out-patient datasets, including outcome prediction, diagnosis classification, drug recommendation, and risk stratification. Swapping standard EHR tokenizers with MedTok improves AUPRC across all EHR models, by 4.10% on MIMIC-III, 4.78% on MIMIC-IV, and 11.30% on EHRShot, with the largest gains in drug recommendation. Beyond EHR modeling, we demonstrate using MedTok tokenizer with medical QA systems. Our results demonstrate the potential of MedTok as a unified tokenizer for medical codes, improving tokenization for medical foundation models.

Unitary convolutions for learning on graphs and groups

Data with geometric structure is ubiquitous in machine learning often arising from fundamental symmetries in a domain, such as permutation-invariance in graphs and translation-invariance in images. Group-convolutional architectures, which encode symmetries as inductive bias, have shown great success in applications, but can suffer from instabilities as their depth increases and often struggle to learn long range dependencies in data. For instance, graph neural networks experience instability due to the convergence of node representations (over-smoothing), which can occur after only a few iterations of message-passing, reducing their effectiveness in downstream tasks. Here, we propose and study unitary group convolutions, which allow for deeper networks that are more stable during training. The main focus of the paper are graph neural networks, where we show that unitary graph convolutions provably avoid over-smoothing. Our experimental results confirm that unitary graph convolutional networks achieve competitive performance on benchmark datasets compared to state-of-the-art graph neural networks. We complement our analysis of the graph domain with the study of general unitary convolutions and analyze their role in enhancing stability in general group convolutional architectures.

Effective Structural Encodings via Local Curvature Profiles

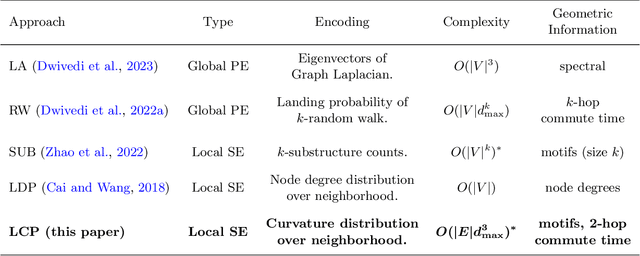
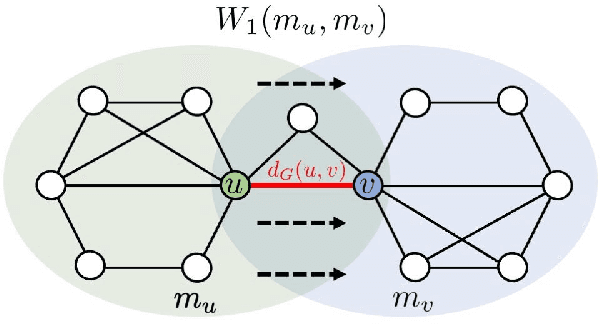
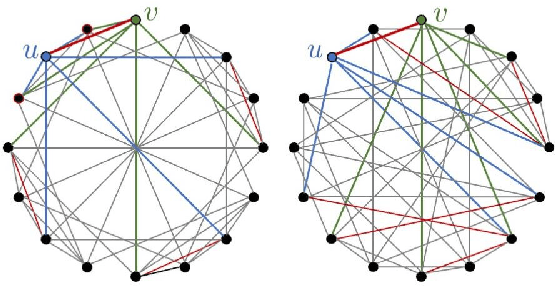
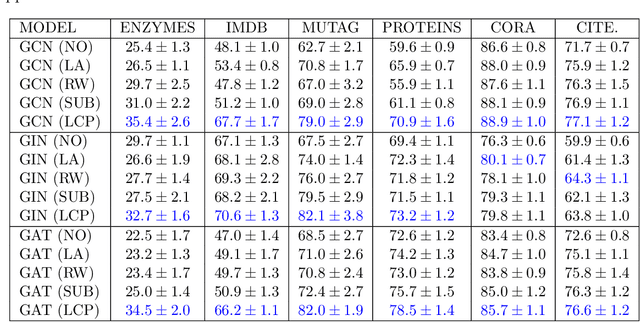
Structural and Positional Encodings can significantly improve the performance of Graph Neural Networks in downstream tasks. Recent literature has begun to systematically investigate differences in the structural properties that these approaches encode, as well as performance trade-offs between them. However, the question of which structural properties yield the most effective encoding remains open. In this paper, we investigate this question from a geometric perspective. We propose a novel structural encoding based on discrete Ricci curvature (Local Curvature Profiles, short LCP) and show that it significantly outperforms existing encoding approaches. We further show that combining local structural encodings, such as LCP, with global positional encodings improves downstream performance, suggesting that they capture complementary geometric information. Finally, we compare different encoding types with (curvature-based) rewiring techniques. Rewiring has recently received a surge of interest due to its ability to improve the performance of Graph Neural Networks by mitigating over-smoothing and over-squashing effects. Our results suggest that utilizing curvature information for structural encodings delivers significantly larger performance increases than rewiring.

Mitigating Over-Smoothing and Over-Squashing using Augmentations of Forman-Ricci Curvature

While Graph Neural Networks (GNNs) have been successfully leveraged for learning on graph-structured data across domains, several potential pitfalls have been described recently. Those include the inability to accurately leverage information encoded in long-range connections (over-squashing), as well as difficulties distinguishing the learned representations of nearby nodes with growing network depth (over-smoothing). An effective way to characterize both effects is discrete curvature: Long-range connections that underlie over-squashing effects have low curvature, whereas edges that contribute to over-smoothing have high curvature. This observation has given rise to rewiring techniques, which add or remove edges to mitigate over-smoothing and over-squashing. Several rewiring approaches utilizing graph characteristics, such as curvature or the spectrum of the graph Laplacian, have been proposed. However, existing methods, especially those based on curvature, often require expensive subroutines and careful hyperparameter tuning, which limits their applicability to large-scale graphs. Here we propose a rewiring technique based on Augmented Forman-Ricci curvature (AFRC), a scalable curvature notation, which can be computed in linear time. We prove that AFRC effectively characterizes over-smoothing and over-squashing effects in message-passing GNNs. We complement our theoretical results with experiments, which demonstrate that the proposed approach achieves state-of-the-art performance while significantly reducing the computational cost in comparison with other methods. Utilizing fundamental properties of discrete curvature, we propose effective heuristics for hyperparameters in curvature-based rewiring, which avoids expensive hyperparameter searches, further improving the scalability of the proposed approach.

Understanding and Mitigating Extrapolation Failures in Physics-Informed Neural Networks

Physics-informed Neural Networks (PINNs) have recently gained popularity in the scientific community due to their effective approximation of partial differential equations (PDEs) using deep neural networks. However, their application has been generally limited to interpolation scenarios, where predictions rely on inputs within the support of the training set. In real-world applications, extrapolation is often required, but the out of domain behavior of PINNs is understudied. In this paper, we provide a detailed investigation of PINNs' extrapolation behavior and provide evidence against several previously held assumptions: we study the effects of different model choices on extrapolation and find that once the model can achieve zero interpolation error, further increases in architecture size or in the number of points sampled have no effect on extrapolation behavior. We also show that for some PDEs, PINNs perform nearly as well in extrapolation as in interpolation. By analyzing the Fourier spectra of the solution functions, we characterize the PDEs that yield favorable extrapolation behavior, and show that the presence of high frequencies in the solution function is not to blame for poor extrapolation behavior. Finally, we propose a transfer learning-based strategy based on our Fourier results, which decreases extrapolation errors in PINNs by up to $82 \%$.