Rethinking the Relationship between Recurrent and Non-Recurrent Neural Networks: A Study in Sparsity

Neural networks (NN) can be divided into two broad categories, recurrent and non-recurrent. Both types of neural networks are popular and extensively studied, but they are often treated as distinct families of machine learning algorithms. In this position paper, we argue that there is a closer relationship between these two types of neural networks than is normally appreciated. We show that many common neural network models, such as Recurrent Neural Networks (RNN), Multi-Layer Perceptrons (MLP), and even deep multi-layer transformers, can all be represented as iterative maps. The close relationship between RNNs and other types of NNs should not be surprising. In particular, RNNs are known to be Turing complete, and therefore capable of representing any computable function (such as any other types of NNs), but herein we argue that the relationship runs deeper and is more practical than this. For example, RNNs are often thought to be more difficult to train than other types of NNs, with RNNs being plagued by issues such as vanishing or exploding gradients. However, as we demonstrate in this paper, MLPs, RNNs, and many other NNs lie on a continuum, and this perspective leads to several insights that illuminate both theoretical and practical aspects of NNs.

Graph Coordinates and Conventional Neural Networks -- An Alternative for Graph Neural Networks

Graph-based data present unique challenges and opportunities for machine learning. Graph Neural Networks (GNNs), and especially those algorithms that capture graph topology through message passing for neighborhood aggregation, have been a leading solution. However, these networks often require substantial computational resources and may not optimally leverage the information contained in the graph's topology, particularly for large-scale or complex graphs. We propose Topology Coordinate Neural Network (TCNN) and Directional Virtual Coordinate Neural Network (DVCNN) as novel and efficient alternatives to message passing GNNs, that directly leverage the graph's topology, sidestepping the computational challenges presented by competing algorithms. Our proposed methods can be viewed as a reprise of classic techniques for graph embedding for neural network feature engineering, but they are novel in that our embedding techniques leverage ideas in Graph Coordinates (GC) that are lacking in current practice. Experimental results, benchmarked against the Open Graph Benchmark Leaderboard, demonstrate that TCNN and DVCNN achieve competitive or superior performance to message passing GNNs. For similar levels of accuracy and ROC-AUC, TCNN and DVCNN need far fewer trainable parameters than contenders of the OGBN Leaderboard. The proposed TCNN architecture requires fewer parameters than any neural network method currently listed in the OGBN Leaderboard for both OGBN-Proteins and OGBN-Products datasets. Conversely, our methods achieve higher performance for a similar number of trainable parameters. By providing an efficient and effective alternative to message passing GNNs, our work expands the toolbox of techniques for graph-based machine learning.

Reconstruction of Fragmented Trajectories of Collective Motion using Hadamard Deep Autoencoders

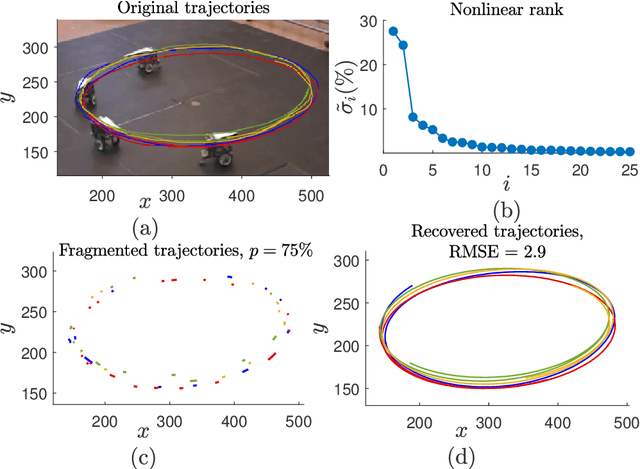
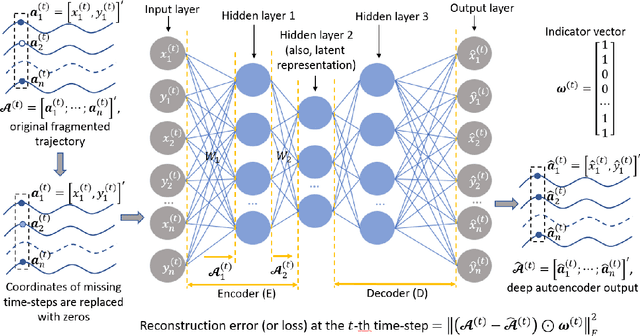
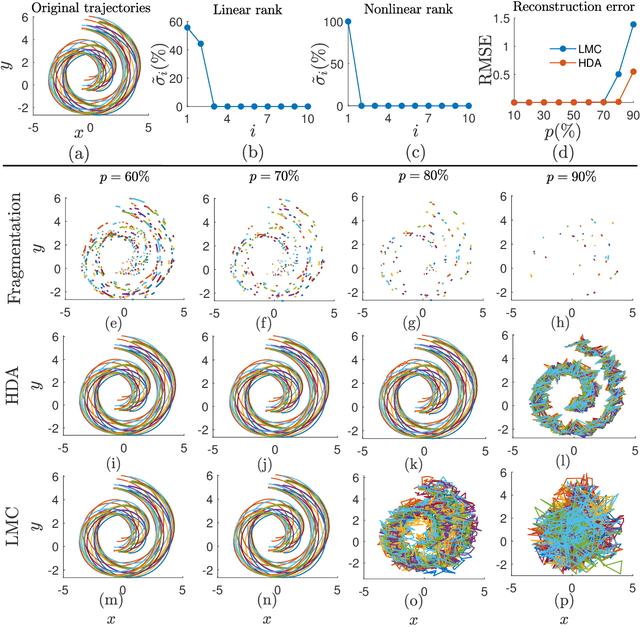
Learning dynamics of collectively moving agents such as fish or humans is an active field in research. Due to natural phenomena such as occlusion and change of illumination, the multi-object methods tracking such dynamics might lose track of the agents where that might result fragmentation in the constructed trajectories. Here, we present an extended deep autoencoder (DA) that we train only on fully observed segments of the trajectories by defining its loss function as the Hadamard product of a binary indicator matrix with the absolute difference between the outputs and the labels. The trajectories of the agents practicing collective motion is low-rank due to mutual interactions and dependencies between the agents that we utilize as the underlying pattern that our Hadamard deep autoencoder (HDA) codes during its training. The performance of our HDA is compared with that of a low-rank matrix completion scheme in the context of fragmented trajectory reconstruction.

A Pre-training Oracle for Predicting Distances in Social Networks

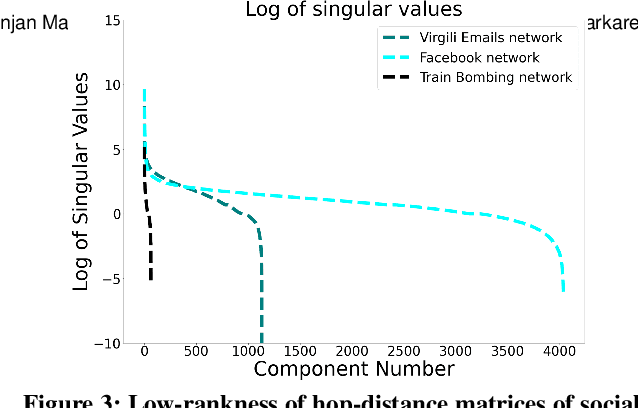
In this paper, we propose a novel method to make distance predictions in real-world social networks. As predicting missing distances is a difficult problem, we take a two-stage approach. Structural parameters for families of synthetic networks are first estimated from a small set of measurements of a real-world network and these synthetic networks are then used to pre-train the predictive neural networks. Since our model first searches for the most suitable synthetic graph parameters which can be used as an "oracle" to create arbitrarily large training data sets, we call our approach "Oracle Search Pre-training" (OSP). For example, many real-world networks exhibit a Power law structure in their node degree distribution, so a Power law model can provide a foundation for the desired oracle to generate synthetic pre-training networks, if the appropriate Power law graph parameters can be estimated. Accordingly, we conduct experiments on real-world Facebook, Email, and Train Bombing networks and show that OSP outperforms models without pre-training, models pre-trained with inaccurate parameters, and other distance prediction schemes such as Low-rank Matrix Completion. In particular, we achieve a prediction error of less than one hop with only 1% of sampled distances from the social network. OSP can be easily extended to other domains such as random networks by choosing an appropriate model to generate synthetic training data, and therefore promises to impact many different network learning problems.

Blind Image Denoising and Inpainting Using Robust Hadamard Autoencoders

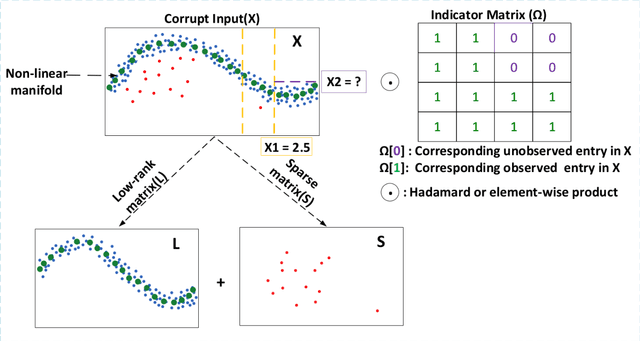
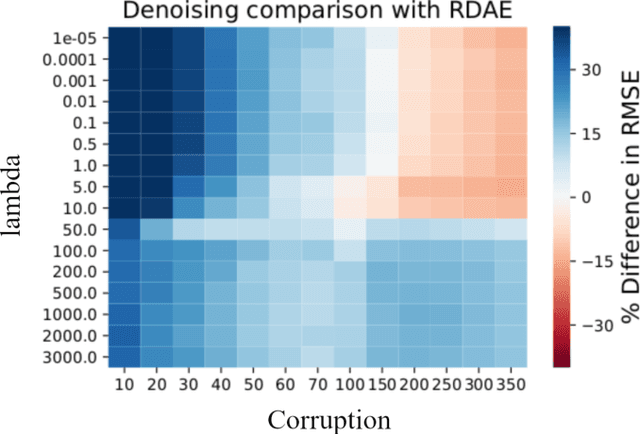
In this paper, we demonstrate how deep autoencoders can be generalized to the case of inpainting and denoising, even when no clean training data is available. In particular, we show how neural networks can be trained to perform all of these tasks simultaneously. While, deep autoencoders implemented by way of neural networks have demonstrated potential for denoising and anomaly detection, standard autoencoders have the drawback that they require access to clean data for training. However, recent work in Robust Deep Autoencoders (RDAEs) shows how autoencoders can be trained to eliminate outliers and noise in a dataset without access to any clean training data. Inspired by this work, we extend RDAEs to the case where data are not only noisy and have outliers, but also only partially observed. Moreover, the dataset we train the neural network on has the properties that all entries have noise, some entries are corrupted by large mistakes, and many entries are not even known. Given such an algorithm, many standard tasks, such as denoising, image inpainting, and unobserved entry imputation can all be accomplished simultaneously within the same framework. Herein we demonstrate these techniques on standard machine learning tasks, such as image inpainting and denoising for the MNIST and CIFAR10 datasets. However, these approaches are not only applicable to image processing problems, but also have wide ranging impacts on datasets arising from real-world problems, such as manufacturing and network processing, where noisy, partially observed data naturally arise.

Machine Learning in LiDAR 3D point clouds

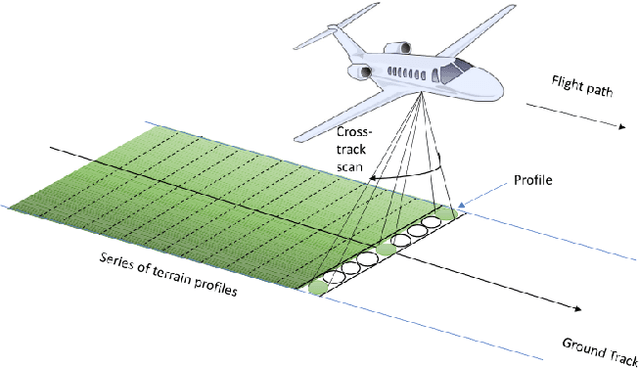
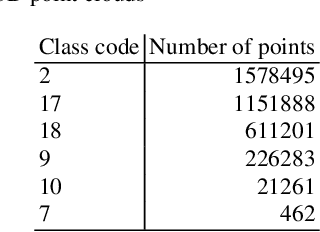
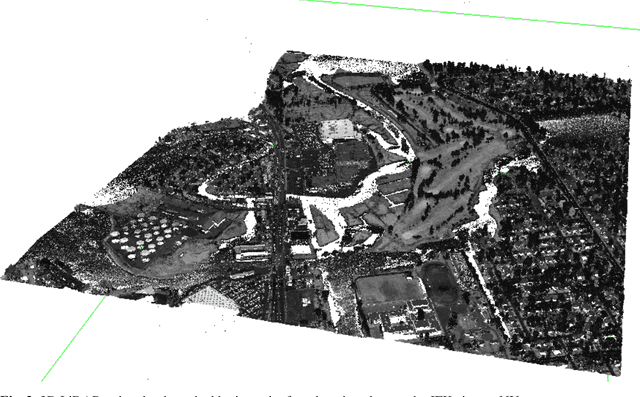
LiDAR point clouds contain measurements of complicated natural scenes and can be used to update digital elevation models, glacial monitoring, detecting faults and measuring uplift detecting, forest inventory, detect shoreline and beach volume changes, landslide risk analysis, habitat mapping, and urban development, among others. A very important application is the classification of the 3D cloud into elementary classes. For example, it can be used to differentiate between vegetation, man-made structures, and water. Our goal is to present a preliminary comparison study for the classification of 3D point cloud LiDAR data that includes several types of feature engineering. In particular, we demonstrate that providing context by augmenting each point in the LiDAR point cloud with information about its neighboring points can improve the performance of downstream learning algorithms. We also experiment with several dimension reduction strategies, ranging from Principal Component Analysis (PCA) to neural network-based auto-encoders, and demonstrate how they affect classification performance in LiDAR point clouds. For instance, we observe that combining feature engineering with a dimension reduction a method such as PCA, there is an improvement in the accuracy of the classification with respect to doing a straightforward classification with the raw data.

A Patch-based Image Denoising Method Using Eigenvectors of the Geodesics' Gramian Matrix

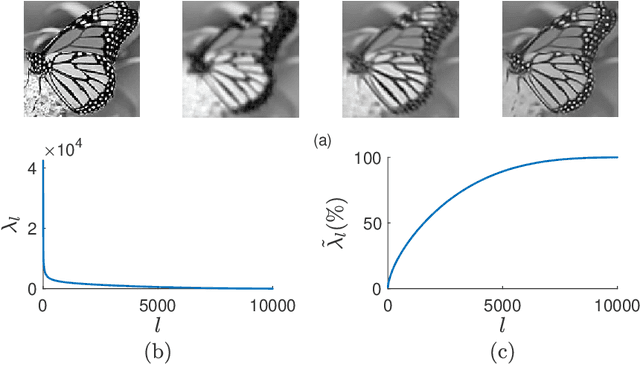
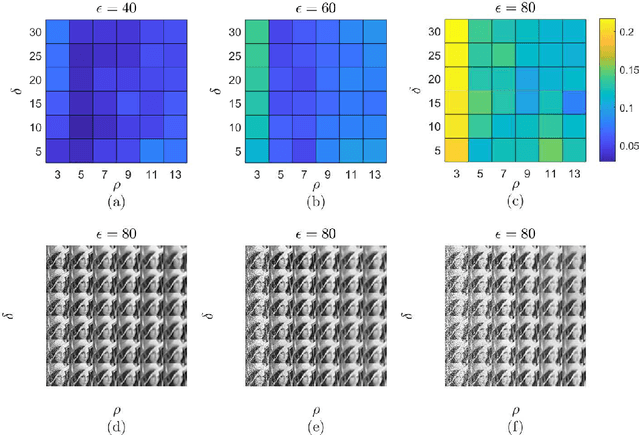
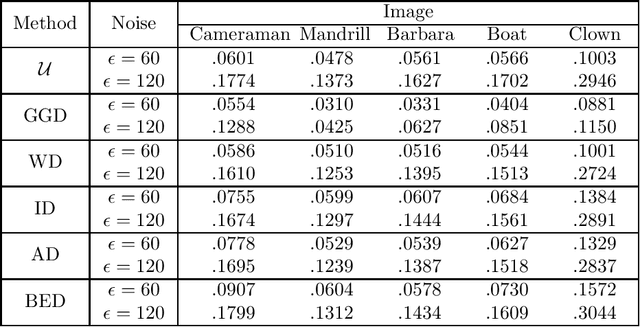
With the sophisticated modern technology in the camera industry, the demand for accurate and visually pleasing images is increasing. However, the quality of images captured by cameras are inevitably degraded by noise. Thus, some processing on images is required to filter out the noise without losing vital image features such as edges, corners, etc. Even though the current literature offers a variety of denoising methods, fidelity and efficiency of their denoising are sometimes uncertain. Thus, here we propose a novel and computationally efficient image denoising method that is capable of producing an accurate output. This method inputs patches partitioned from the image rather than pixels that are well known for preserving image smoothness. Then, it performs denoising on the manifold underlying the patch-space rather than that in the image domain to better preserve the features across the whole image. We validate the performance of this method against benchmark image processing methods.

Bounded Manifold Completion

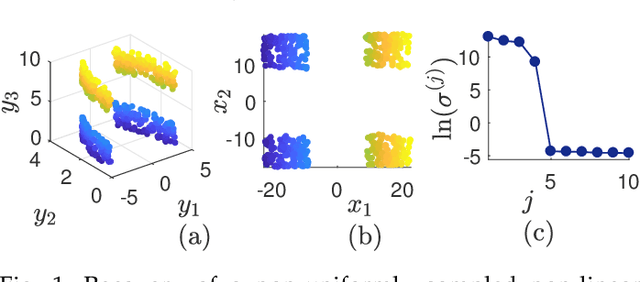
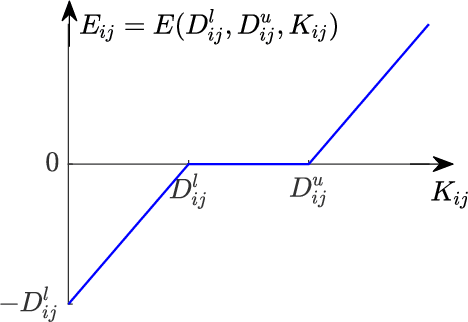
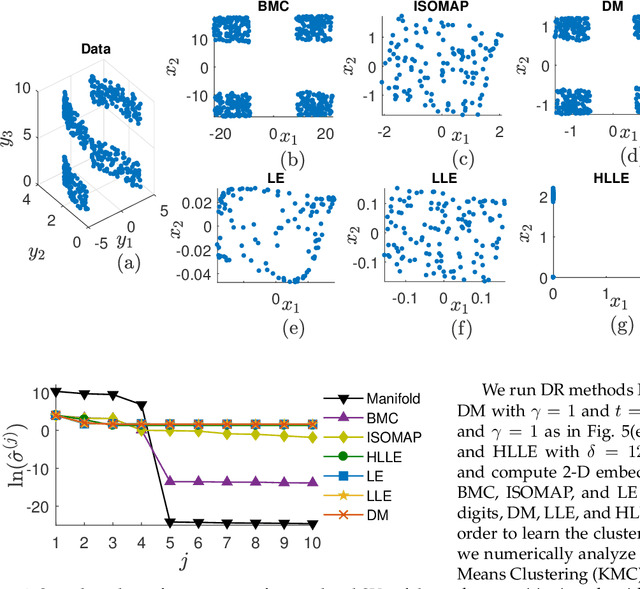
Nonlinear dimensionality reduction or, equivalently, the approximation of high-dimensional data using a low-dimensional nonlinear manifold is an active area of research. In this paper, we will present a thematically different approach to detect the existence of a low-dimensional manifold of a given dimension that lies within a set of bounds derived from a given point cloud. A matrix representing the appropriately defined distances on a low-dimensional manifold is low-rank, and our method is based on current techniques for recovering a partially observed matrix from a small set of fully observed entries that can be implemented as a low-rank Matrix Completion (MC) problem. MC methods are currently used to solve challenging real-world problems, such as image inpainting and recommender systems, and we leverage extent efficient optimization techniques that use a nuclear norm convex relaxation as a surrogate for non-convex and discontinuous rank minimization. Our proposed method provides several advantages over current nonlinear dimensionality reduction techniques, with the two most important being theoretical guarantees on the detection of low-dimensional embeddings and robustness to non-uniformity in the sampling of the manifold. We validate the performance of this approach using both a theoretical analysis as well as synthetic and real-world benchmark datasets.

Dimension Estimation Using Autoencoders

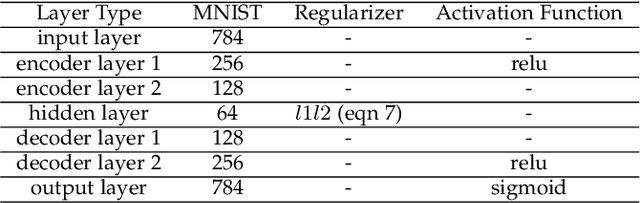
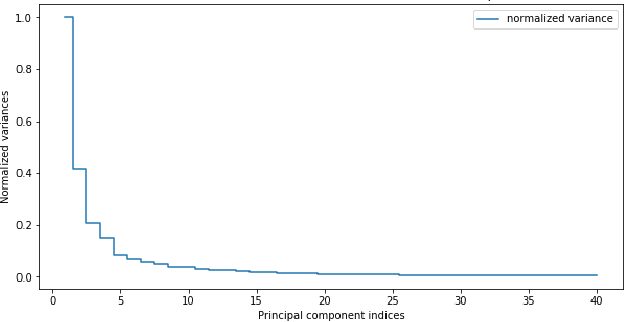
Dimension Estimation (DE) and Dimension Reduction (DR) are two closely related topics, but with quite different goals. In DE, one attempts to estimate the intrinsic dimensionality or number of latent variables in a set of measurements of a random vector. However, in DR, one attempts to project a random vector, either linearly or non-linearly, to a lower dimensional space that preserves the information contained in the original higher dimensional space. Of course, these two ideas are quite closely linked since, for example, doing DR to a dimension smaller than suggested by DE will likely lead to information loss. Accordingly, in this paper we will focus on a particular class of deep neural networks called autoencoders which are used extensively for DR but are less well studied for DE. We show that several important questions arise when using autoencoders for DE, above and beyond those that arise for more classic DR/DE techniques such as Principal Component Analysis. We address autoencoder architectural choices and regularization techniques that allow one to transform autoencoder latent layer representations into estimates of intrinsic dimension.

A Nonlinear Dimensionality Reduction Framework Using Smooth Geodesics

Existing dimensionality reduction methods are adept at revealing hidden underlying manifolds arising from high-dimensional data and thereby producing a low-dimensional representation. However, the smoothness of the manifolds produced by classic techniques over sparse and noisy data is not guaranteed. In fact, the embedding generated using such data may distort the geometry of the manifold and thereby produce an unfaithful embedding. Herein, we propose a framework for nonlinear dimensionality reduction that generates a manifold in terms of smooth geodesics that is designed to treat problems in which manifold measurements are either sparse or corrupted by noise. Our method generates a network structure for given high-dimensional data using a nearest neighbors search and then produces piecewise linear shortest paths that are defined as geodesics. Then, we fit points in each geodesic by a smoothing spline to emphasize the smoothness. The robustness of this approach for sparse and noisy datasets is demonstrated by the implementation of the method on synthetic and real-world datasets.