Efficient and Robust Remote Sensing Image Denoising Using Randomized Approximation of Geodesics' Gramian on the Manifold Underlying the Patch Space

Remote sensing images are widely utilized in many disciplines such as feature recognition and scene semantic segmentation. However, due to environmental factors and the issues of the imaging system, the image quality is often degraded which may impair subsequent visual tasks. Even though denoising remote sensing images plays an essential role before applications, the current denoising algorithms fail to attain optimum performance since these images possess complex features in the texture. Denoising frameworks based on artificial neural networks have shown better performance; however, they require exhaustive training with heterogeneous samples that extensively consume resources like power, memory, computation, and latency. Thus, here we present a computationally efficient and robust remote sensing image denoising method that doesn't require additional training samples. This method partitions patches of a remote-sensing image in which a low-rank manifold, representing the noise-free version of the image, underlies the patch space. An efficient and robust approach to revealing this manifold is a randomized approximation of the singular value spectrum of the geodesics' Gramian matrix of the patch space. The method asserts a unique emphasis on each color channel during denoising so the three denoised channels are merged to produce the final image.

Efficient Noise Filtration of Images by Low-Rank Singular Vector Approximations of Geodesics' Gramian Matrix

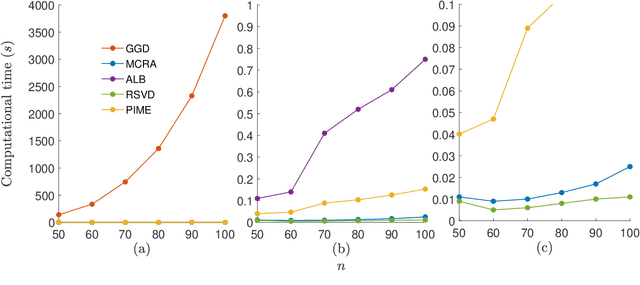
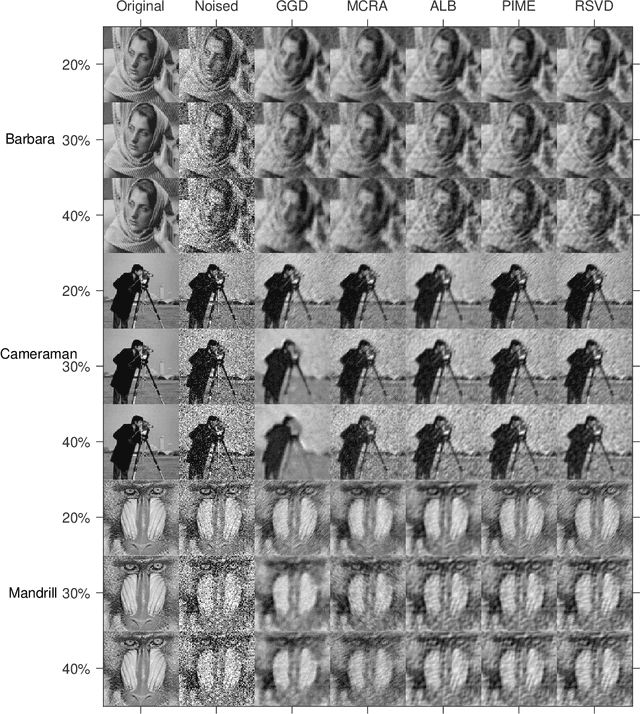
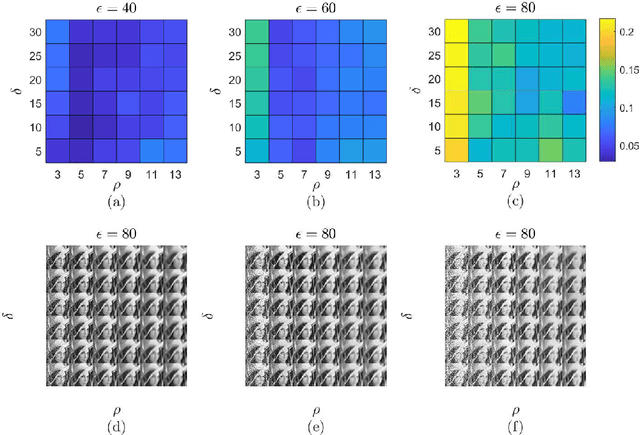
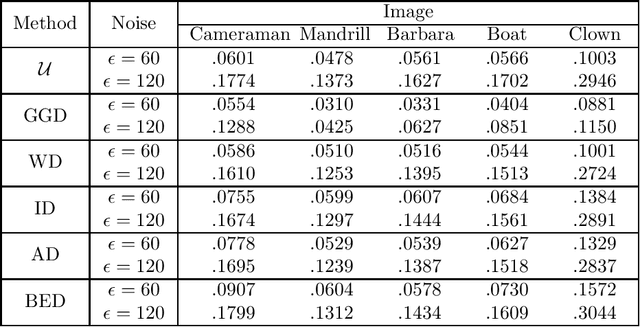
Modern society is interested in capturing high-resolution and fine-quality images due to the surge of sophisticated cameras. However, the noise contamination in the images not only inferior people's expectations but also conversely affects the subsequent processes if such images are utilized in computer vision tasks such as remote sensing, object tracking, etc. Even though noise filtration plays an essential role, real-time processing of a high-resolution image is limited by the hardware limitations of the image-capturing instruments. Geodesic Gramian Denoising (GGD) is a manifold-based noise filtering method that we introduced in our past research which utilizes a few prominent singular vectors of the geodesics' Gramian matrix for the noise filtering process. The applicability of GDD is limited as it encounters $\mathcal{O}(n^6)$ when denoising a given image of size $n\times n$ since GGD computes the prominent singular vectors of a $n^2 \times n^2$ data matrix that is implemented by singular value decomposition (SVD). In this research, we increase the efficiency of our GGD framework by replacing its SVD step with four diverse singular vector approximation techniques. Here, we compare both the computational time and the noise filtering performance between the four techniques integrated into GGD.

Fraud Detection Using Optimized Machine Learning Tools Under Imbalance Classes

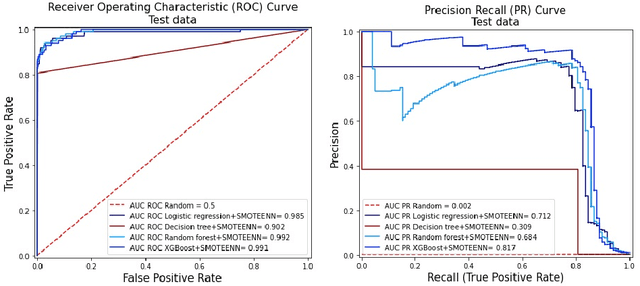
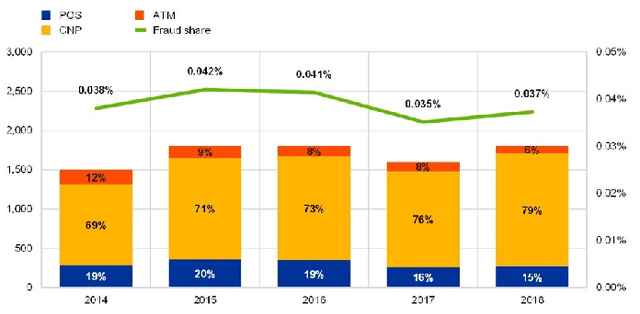
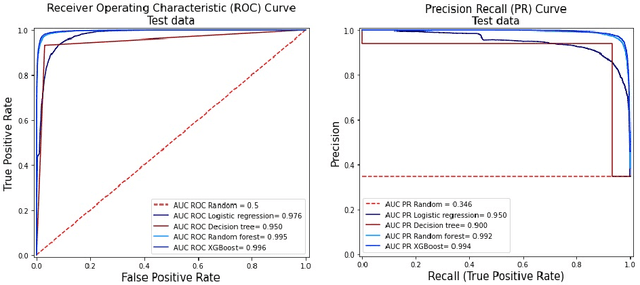
Fraud detection is a challenging task due to the changing nature of fraud patterns over time and the limited availability of fraud examples to learn such sophisticated patterns. Thus, fraud detection with the aid of smart versions of machine learning (ML) tools is essential to assure safety. Fraud detection is a primary ML classification task; however, the optimum performance of the corresponding ML tool relies on the usage of the best hyperparameter values. Moreover, classification under imbalanced classes is quite challenging as it causes poor performance in minority classes, which most ML classification techniques ignore. Thus, we investigate four state-of-the-art ML techniques, namely, logistic regression, decision trees, random forest, and extreme gradient boost, that are suitable for handling imbalance classes to maximize precision and simultaneously reduce false positives. First, these classifiers are trained on two original benchmark unbalanced fraud detection datasets, namely, phishing website URLs and fraudulent credit card transactions. Then, three synthetically balanced datasets are produced for each original data set by implementing the sampling frameworks, namely, RandomUnderSampler, SMOTE, and SMOTEENN. The optimum hyperparameters for all the 16 experiments are revealed using the method RandomzedSearchCV. The validity of the 16 approaches in the context of fraud detection is compared using two benchmark performance metrics, namely, area under the curve of receiver operating characteristics (AUC ROC) and area under the curve of precision and recall (AUC PR). For both phishing website URLs and credit card fraud transaction datasets, the results indicate that extreme gradient boost trained on the original data shows trustworthy performance in the imbalanced dataset and manages to outperform the other three methods in terms of both AUC ROC and AUC PR.

Real-time Forecasting of Time Series in Financial Markets Using Sequentially Trained Many-to-one LSTMs

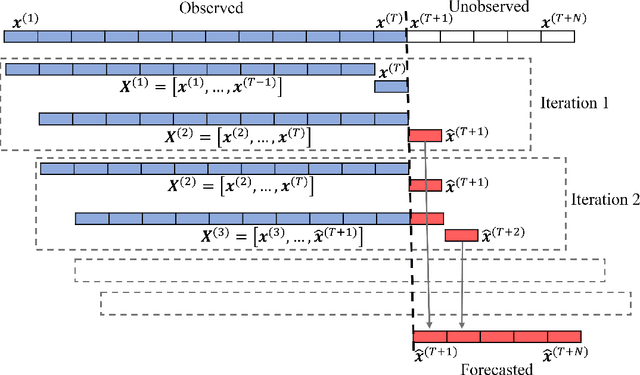
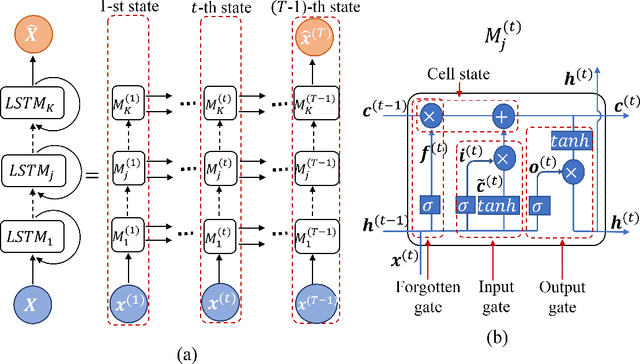
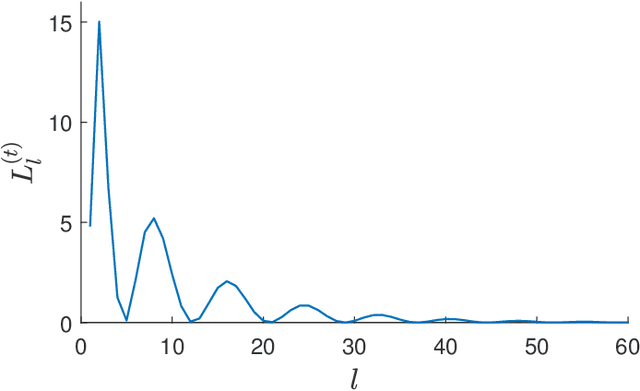
Financial markets are highly complex and volatile; thus, learning about such markets for the sake of making predictions is vital to make early alerts about crashes and subsequent recoveries. People have been using learning tools from diverse fields such as financial mathematics and machine learning in the attempt of making trustworthy predictions on such markets. However, the accuracy of such techniques had not been adequate until artificial neural network (ANN) frameworks were developed. Moreover, making accurate real-time predictions of financial time series is highly subjective to the ANN architecture in use and the procedure of training it. Long short-term memory (LSTM) is a member of the recurrent neural network family which has been widely utilized for time series predictions. Especially, we train two LSTMs with a known length, say $T$ time steps, of previous data and predict only one time step ahead. At each iteration, while one LSTM is employed to find the best number of epochs, the second LSTM is trained only for the best number of epochs to make predictions. We treat the current prediction as in the training set for the next prediction and train the same LSTM. While classic ways of training result in more error when the predictions are made further away in the test period, our approach is capable of maintaining a superior accuracy as training increases when it proceeds through the testing period. The forecasting accuracy of our approach is validated using three time series from each of the three diverse financial markets: stock, cryptocurrency, and commodity. The results are compared with those of an extended Kalman filter, an autoregressive model, and an autoregressive integrated moving average model.

Geodesic Gramian Denoising Applied to the Images Contaminated With Noise Sampled From Diverse Probability Distributions

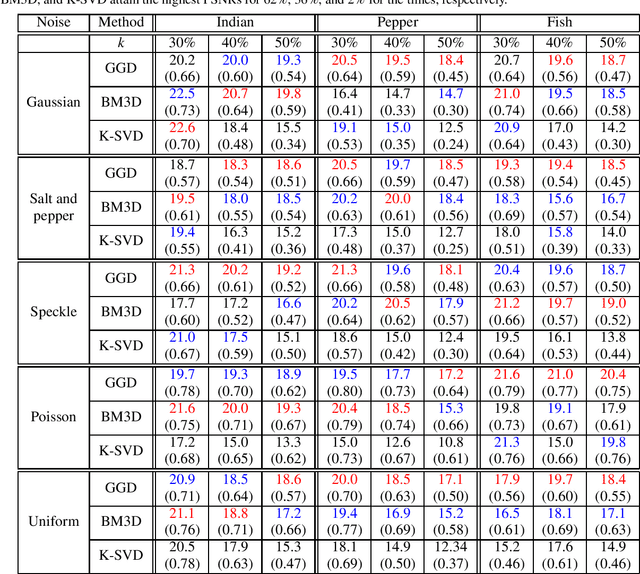
As quotidian use of sophisticated cameras surges, people in modern society are more interested in capturing fine-quality images. However, the quality of the images might be inferior to people's expectations due to the noise contamination in the images. Thus, filtering out the noise while preserving vital image features is an essential requirement. Current existing denoising methods have their own assumptions on the probability distribution in which the contaminated noise is sampled for the method to attain its expected denoising performance. In this paper, we utilize our recent Gramian-based filtering scheme to remove noise sampled from five prominent probability distributions from selected images. This method preserves image smoothness by adopting patches partitioned from the image, rather than pixels, and retains vital image features by performing denoising on the manifold underlying the patch space rather than in the image domain. We validate its denoising performance, using three benchmark computer vision test images applied to two state-of-the-art denoising methods, namely BM3D and K-SVD.

Recurrent Neural Networks for Dynamical Systems: Applications to Ordinary Differential Equations, Collective Motion, and Hydrological Modeling

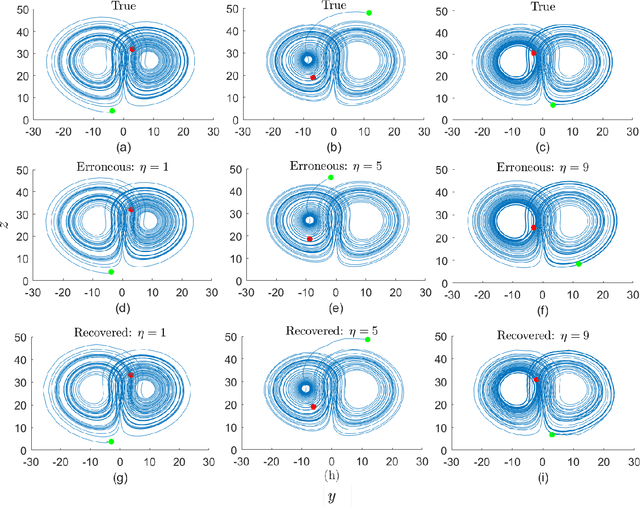
Classical methods of solving spatiotemporal dynamical systems include statistical approaches such as autoregressive integrated moving average, which assume linear and stationary relationships between systems' previous outputs. Development and implementation of linear methods are relatively simple, but they often do not capture non-linear relationships in the data. Thus, artificial neural networks (ANNs) are receiving attention from researchers in analyzing and forecasting dynamical systems. Recurrent neural networks (RNN), derived from feed-forward ANNs, use internal memory to process variable-length sequences of inputs. This allows RNNs to applicable for finding solutions for a vast variety of problems in spatiotemporal dynamical systems. Thus, in this paper, we utilize RNNs to treat some specific issues associated with dynamical systems. Specifically, we analyze the performance of RNNs applied to three tasks: reconstruction of correct Lorenz solutions for a system with a formulation error, reconstruction of corrupted collective motion trajectories, and forecasting of streamflow time series possessing spikes, representing three fields, namely, ordinary differential equations, collective motion, and hydrological modeling, respectively. We train and test RNNs uniquely in each task to demonstrate the broad applicability of RNNs in reconstruction and forecasting the dynamics of dynamical systems.

Reconstruction of Fragmented Trajectories of Collective Motion using Hadamard Deep Autoencoders

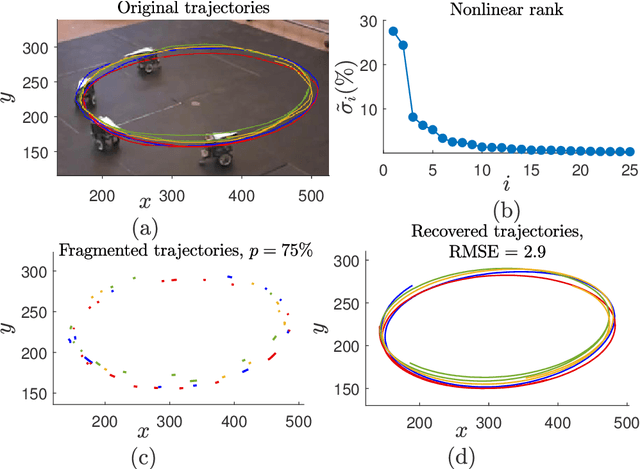
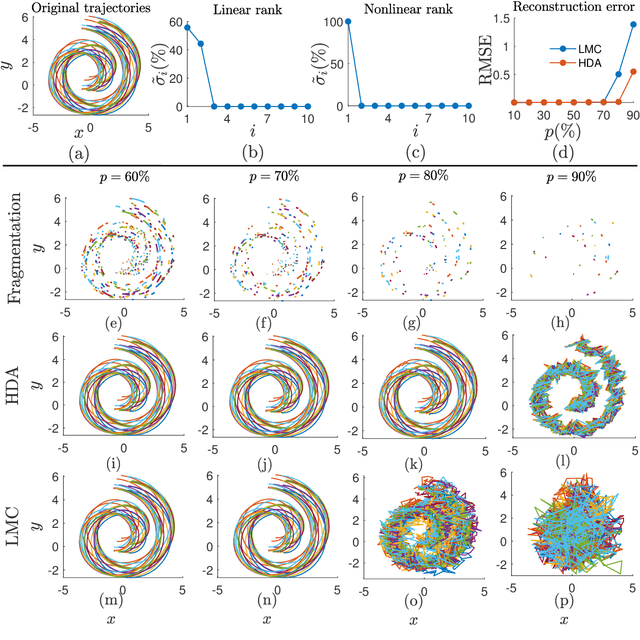
Learning dynamics of collectively moving agents such as fish or humans is an active field in research. Due to natural phenomena such as occlusion and change of illumination, the multi-object methods tracking such dynamics might lose track of the agents where that might result fragmentation in the constructed trajectories. Here, we present an extended deep autoencoder (DA) that we train only on fully observed segments of the trajectories by defining its loss function as the Hadamard product of a binary indicator matrix with the absolute difference between the outputs and the labels. The trajectories of the agents practicing collective motion is low-rank due to mutual interactions and dependencies between the agents that we utilize as the underlying pattern that our Hadamard deep autoencoder (HDA) codes during its training. The performance of our HDA is compared with that of a low-rank matrix completion scheme in the context of fragmented trajectory reconstruction.

A Patch-based Image Denoising Method Using Eigenvectors of the Geodesics' Gramian Matrix

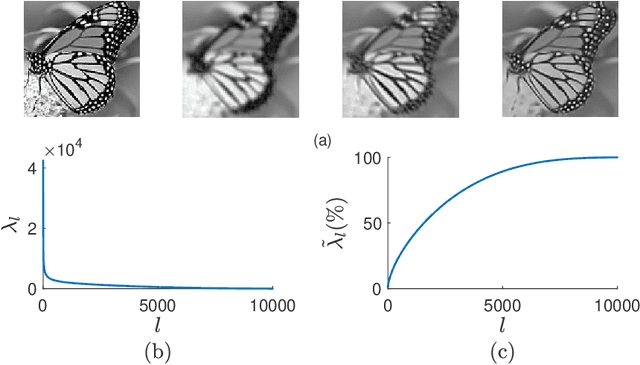
With the sophisticated modern technology in the camera industry, the demand for accurate and visually pleasing images is increasing. However, the quality of images captured by cameras are inevitably degraded by noise. Thus, some processing on images is required to filter out the noise without losing vital image features such as edges, corners, etc. Even though the current literature offers a variety of denoising methods, fidelity and efficiency of their denoising are sometimes uncertain. Thus, here we propose a novel and computationally efficient image denoising method that is capable of producing an accurate output. This method inputs patches partitioned from the image rather than pixels that are well known for preserving image smoothness. Then, it performs denoising on the manifold underlying the patch-space rather than that in the image domain to better preserve the features across the whole image. We validate the performance of this method against benchmark image processing methods.

Bounded Manifold Completion

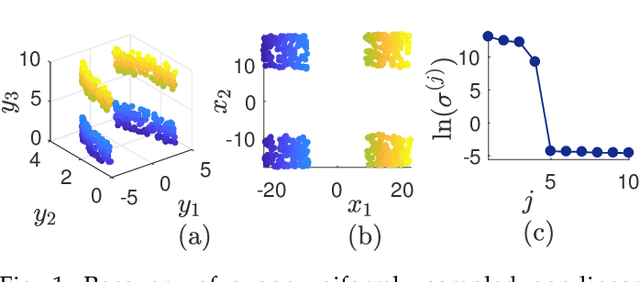
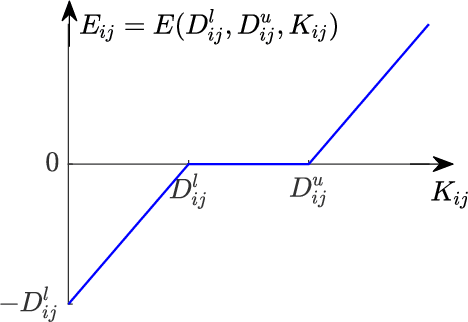
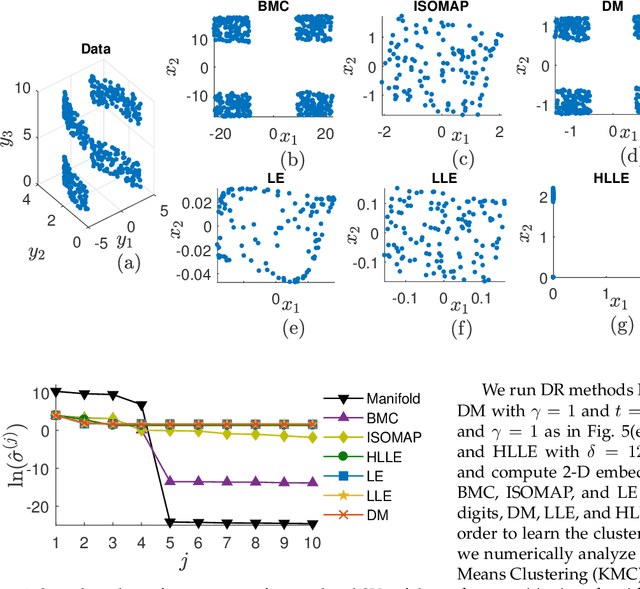
Nonlinear dimensionality reduction or, equivalently, the approximation of high-dimensional data using a low-dimensional nonlinear manifold is an active area of research. In this paper, we will present a thematically different approach to detect the existence of a low-dimensional manifold of a given dimension that lies within a set of bounds derived from a given point cloud. A matrix representing the appropriately defined distances on a low-dimensional manifold is low-rank, and our method is based on current techniques for recovering a partially observed matrix from a small set of fully observed entries that can be implemented as a low-rank Matrix Completion (MC) problem. MC methods are currently used to solve challenging real-world problems, such as image inpainting and recommender systems, and we leverage extent efficient optimization techniques that use a nuclear norm convex relaxation as a surrogate for non-convex and discontinuous rank minimization. Our proposed method provides several advantages over current nonlinear dimensionality reduction techniques, with the two most important being theoretical guarantees on the detection of low-dimensional embeddings and robustness to non-uniformity in the sampling of the manifold. We validate the performance of this approach using both a theoretical analysis as well as synthetic and real-world benchmark datasets.

A Nonlinear Dimensionality Reduction Framework Using Smooth Geodesics

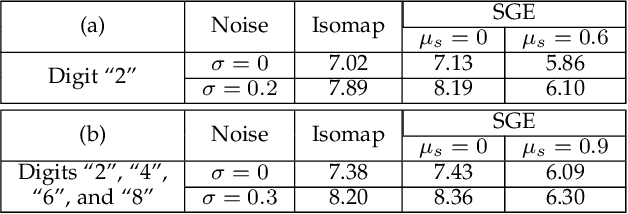
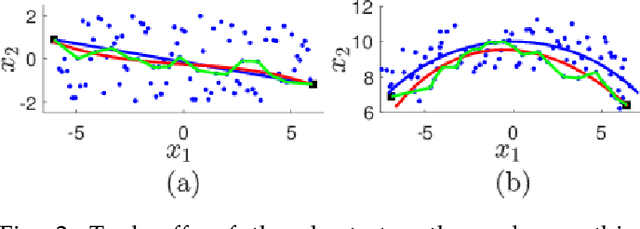
Existing dimensionality reduction methods are adept at revealing hidden underlying manifolds arising from high-dimensional data and thereby producing a low-dimensional representation. However, the smoothness of the manifolds produced by classic techniques over sparse and noisy data is not guaranteed. In fact, the embedding generated using such data may distort the geometry of the manifold and thereby produce an unfaithful embedding. Herein, we propose a framework for nonlinear dimensionality reduction that generates a manifold in terms of smooth geodesics that is designed to treat problems in which manifold measurements are either sparse or corrupted by noise. Our method generates a network structure for given high-dimensional data using a nearest neighbors search and then produces piecewise linear shortest paths that are defined as geodesics. Then, we fit points in each geodesic by a smoothing spline to emphasize the smoothness. The robustness of this approach for sparse and noisy datasets is demonstrated by the implementation of the method on synthetic and real-world datasets.