Tree-based Learning for High-Fidelity Prediction of Chaos

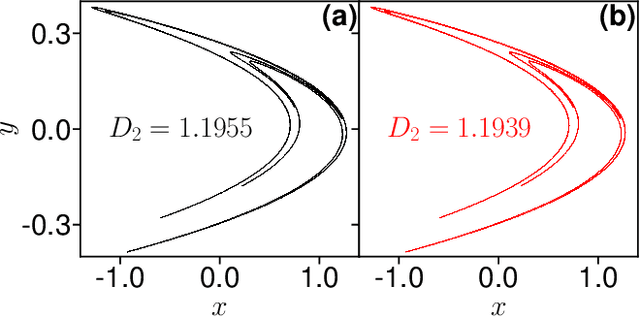
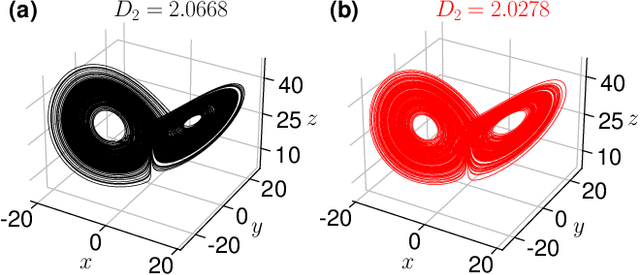
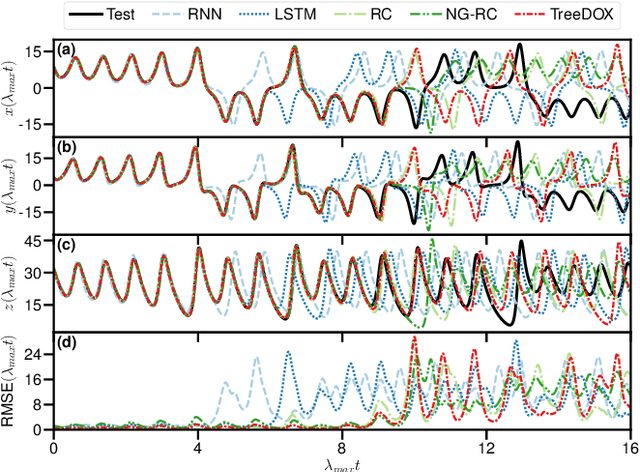
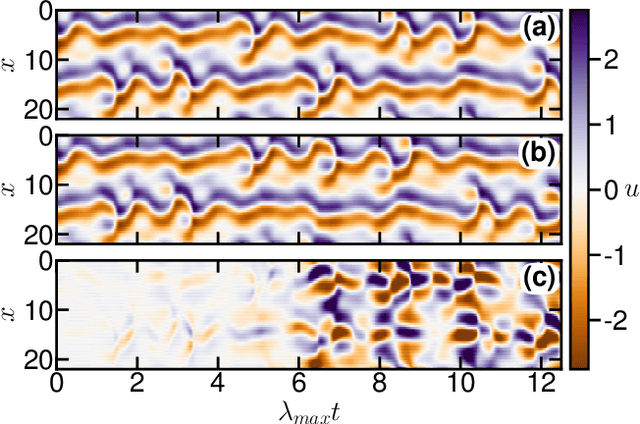
Model-free forecasting of the temporal evolution of chaotic systems is crucial but challenging. Existing solutions require hyperparameter tuning, significantly hindering their wider adoption. In this work, we introduce a tree-based approach not requiring hyperparameter tuning: TreeDOX. It uses time delay overembedding as explicit short-term memory and Extra-Trees Regressors to perform feature reduction and forecasting. We demonstrate the state-of-the-art performance of TreeDOX using the Henon map, Lorenz and Kuramoto-Sivashinsky systems, and the real-world Southern Oscillation Index.

Analysis of tidal flows through the Strait of Gibraltar using Dynamic Mode Decomposition

The Strait of Gibraltar is a region characterized by intricate oceanic sub-mesoscale features, influenced by topography, tidal forces, instabilities, and nonlinear hydraulic processes, all governed by the nonlinear equations of fluid motion. In this study, we aim to uncover the underlying physics of these phenomena within 3D MIT general circulation model simulations, including waves, eddies, and gyres. To achieve this, we employ Dynamic Mode Decomposition (DMD) to break down simulation snapshots into Koopman modes, with distinct exponential growth/decay rates and oscillation frequencies. Our objectives encompass evaluating DMD's efficacy in capturing known features, unveiling new elements, ranking modes, and exploring order reduction. We also introduce modifications to enhance DMD's robustness, numerical accuracy, and robustness of eigenvalues. DMD analysis yields a comprehensive understanding of flow patterns, internal wave formation, and the dynamics of the Strait of Gibraltar, its meandering behaviors, and the formation of a secondary gyre, notably the Western Alboran Gyre, as well as the propagation of Kelvin and coastal-trapped waves along the African coast. In doing so, it significantly advances our comprehension of intricate oceanographic phenomena and underscores the immense utility of DMD as an analytical tool for such complex datasets, suggesting that DMD could serve as a valuable addition to the toolkit of oceanographers.

Autoencoding for the 'Good Dictionary' of eigen pairs of the Koopman Operator

Reduced order modelling relies on representing complex dynamical systems using simplified modes, which can be achieved through Koopman operator analysis. However, computing Koopman eigen pairs for high-dimensional observable data can be inefficient. This paper proposes using deep autoencoders, a type of deep learning technique, to perform non-linear geometric transformations on raw data before computing Koopman eigen vectors. The encoded data produced by the deep autoencoder is diffeomorphic to a manifold of the dynamical system, and has a significantly lower dimension than the raw data. To handle high-dimensional time series data, Takens's time delay embedding is presented as a pre-processing technique. The paper concludes by presenting examples of these techniques in action.

Recurrent Neural Networks for Dynamical Systems: Applications to Ordinary Differential Equations, Collective Motion, and Hydrological Modeling

Classical methods of solving spatiotemporal dynamical systems include statistical approaches such as autoregressive integrated moving average, which assume linear and stationary relationships between systems' previous outputs. Development and implementation of linear methods are relatively simple, but they often do not capture non-linear relationships in the data. Thus, artificial neural networks (ANNs) are receiving attention from researchers in analyzing and forecasting dynamical systems. Recurrent neural networks (RNN), derived from feed-forward ANNs, use internal memory to process variable-length sequences of inputs. This allows RNNs to applicable for finding solutions for a vast variety of problems in spatiotemporal dynamical systems. Thus, in this paper, we utilize RNNs to treat some specific issues associated with dynamical systems. Specifically, we analyze the performance of RNNs applied to three tasks: reconstruction of correct Lorenz solutions for a system with a formulation error, reconstruction of corrupted collective motion trajectories, and forecasting of streamflow time series possessing spikes, representing three fields, namely, ordinary differential equations, collective motion, and hydrological modeling, respectively. We train and test RNNs uniquely in each task to demonstrate the broad applicability of RNNs in reconstruction and forecasting the dynamics of dynamical systems.

Randomized Projection Learning Method forDynamic Mode Decomposition

A data-driven analysis method known as dynamic mode decomposition (DMD) approximates the linear Koopman operator on projected space. In the spirit of Johnson-Lindenstrauss Lemma, we will use random projection to estimate the DMD modes in reduced dimensional space. In practical applications, snapshots are in high dimensional observable space and the DMD operator matrix is massive. Hence, computing DMD with the full spectrum is infeasible, so our main computational goal is estimating the eigenvalue and eigenvectors of the DMD operator in a projected domain. We will generalize the current algorithm to estimate a projected DMD operator. We focus on a powerful and simple random projection algorithm that will reduce the computational and storage cost. While clearly, a random projection simplifies the algorithmic complexity of a detailed optimal projection, as we will show, generally the results can be excellent nonetheless, and quality understood through a well-developed theory of random projections. We will demonstrate that modes can be calculated for a low cost by the projected data with sufficient dimension. Keyword: Koopman Operator, Dynamic Mode Decomposition(DMD), Johnson-Lindenstrauss Lemma, Random Projection, Data-driven method.

On Geometry of Information Flow for Causal Inference

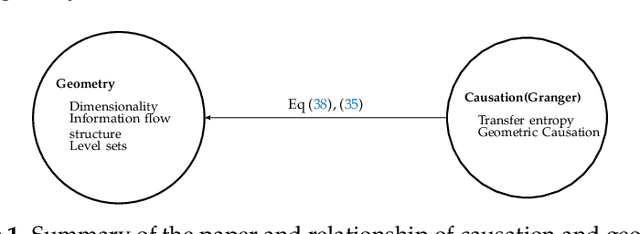
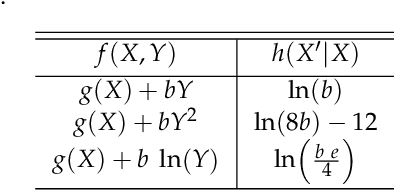
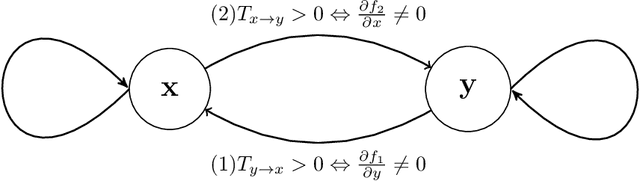
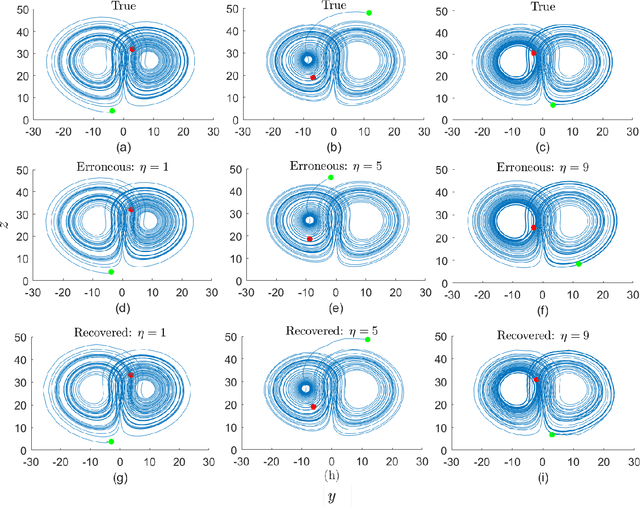
Causal inference is perhaps one of the most fundamental concepts in science, beginning originally from the works of some of the ancient philosophers, through today, but also weaved strongly in current work from statisticians, machine learning experts, and scientists from many other fields. This paper takes the perspective of information flow, which includes the Nobel prize winning work on Granger-causality, and the recently highly popular transfer entropy, these being probabilistic in nature. Our main contribution will be to develop analysis tools that will allow a geometric interpretation of information flow as a causal inference indicated by positive transfer entropy. We will describe the effective dimensionality of an underlying manifold as projected into the outcome space that summarizes information flow. Therefore contrasting the probabilistic and geometric perspectives, we will introduce a new measure of causal inference based on the fractal correlation dimension conditionally applied to competing explanations of future forecasts, which we will write $GeoC_{y\rightarrow x}$. This avoids some of the boundedness issues that we show exist for the transfer entropy, $T_{y\rightarrow x}$. We will highlight our discussions with data developed from synthetic models of successively more complex nature: then include the H\'{e}non map example, and finally a real physiological example relating breathing and heart rate function. Keywords: Causal Inference; Transfer Entropy; Differential Entropy; Correlation Dimension; Pinsker's Inequality; Frobenius-Perron operator.

A Nonlinear Dimensionality Reduction Framework Using Smooth Geodesics

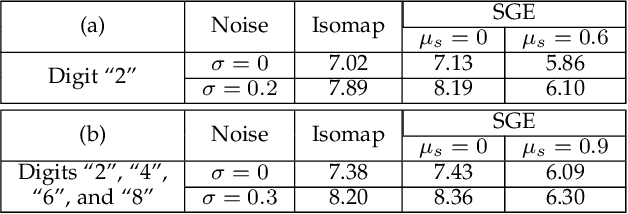
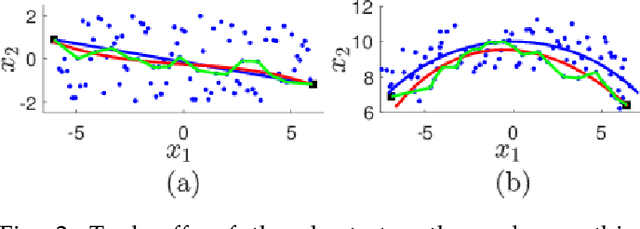
Existing dimensionality reduction methods are adept at revealing hidden underlying manifolds arising from high-dimensional data and thereby producing a low-dimensional representation. However, the smoothness of the manifolds produced by classic techniques over sparse and noisy data is not guaranteed. In fact, the embedding generated using such data may distort the geometry of the manifold and thereby produce an unfaithful embedding. Herein, we propose a framework for nonlinear dimensionality reduction that generates a manifold in terms of smooth geodesics that is designed to treat problems in which manifold measurements are either sparse or corrupted by noise. Our method generates a network structure for given high-dimensional data using a nearest neighbors search and then produces piecewise linear shortest paths that are defined as geodesics. Then, we fit points in each geodesic by a smoothing spline to emphasize the smoothness. The robustness of this approach for sparse and noisy datasets is demonstrated by the implementation of the method on synthetic and real-world datasets.

Go With the Flow, on Jupiter and Snow. Coherence From Model-Free Video Data without Trajectories

Viewing a data set such as the clouds of Jupiter, coherence is readily apparent to human observers, especially the Great Red Spot, but also other great storms and persistent structures. There are now many different definitions and perspectives mathematically describing coherent structures, but we will take an image processing perspective here. We describe an image processing perspective inference of coherent sets from a fluidic system directly from image data, without attempting to first model underlying flow fields, related to a concept in image processing called motion tracking. In contrast to standard spectral methods for image processing which are generally related to a symmetric affinity matrix, leading to standard spectral graph theory, we need a not symmetric affinity which arises naturally from the underlying arrow of time. We develop an anisotropic, directed diffusion operator corresponding to flow on a directed graph, from a directed affinity matrix developed with coherence in mind, and corresponding spectral graph theory from the graph Laplacian. Our methodology is not offered as more accurate than other traditional methods of finding coherent sets, but rather our approach works with alternative kinds of data sets, in the absence of vector field. Our examples will include partitioning the weather and cloud structures of Jupiter, and a local to Potsdam, N.Y. lake-effect snow event on Earth, as well as the benchmark test double-gyre system.

Detecting phase transitions in collective behavior using manifold's curvature

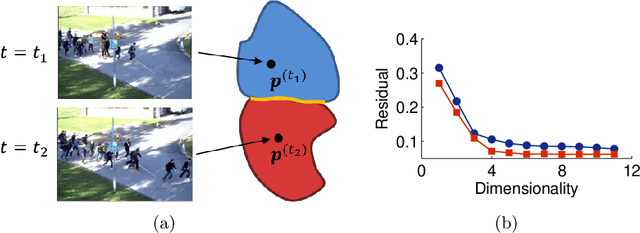
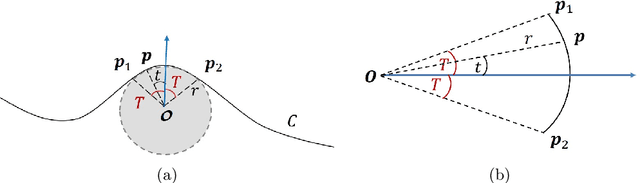
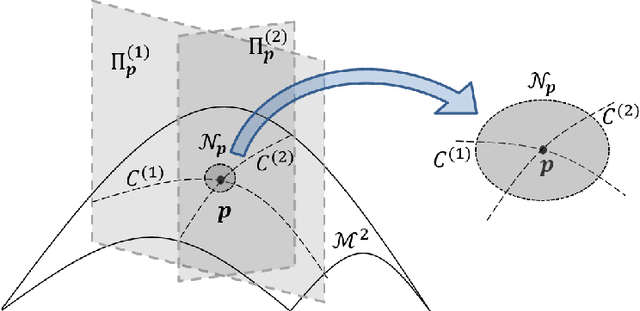
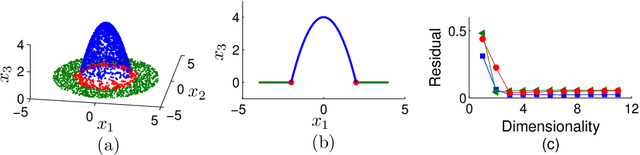
If a given behavior of a multi-agent system restricts the phase variable to a invariant manifold, then we define a phase transition as change of physical characteristics such as speed, coordination, and structure. We define such a phase transition as splitting an underlying manifold into two sub-manifolds with distinct dimensionalities around the singularity where the phase transition physically exists. Here, we propose a method of detecting phase transitions and splitting the manifold into phase transitions free sub-manifolds. Therein, we utilize a relationship between curvature and singular value ratio of points sampled in a curve, and then extend the assertion into higher-dimensions using the shape operator. Then we attest that the same phase transition can also be approximated by singular value ratios computed locally over the data in a neighborhood on the manifold. We validate the phase transitions detection method using one particle simulation and three real world examples.

Dimensionality Reduction of Collective Motion by Principal Manifolds

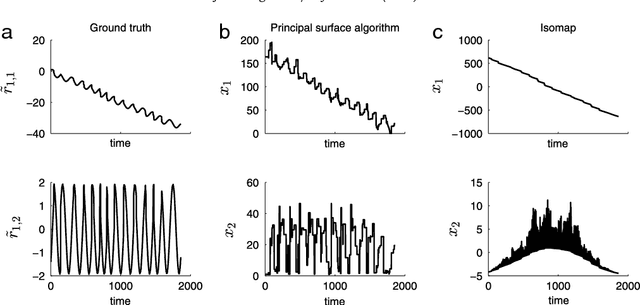
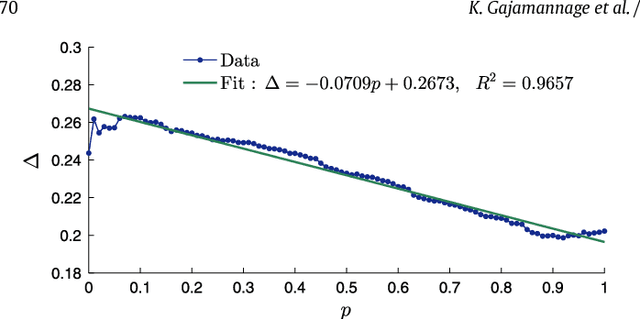
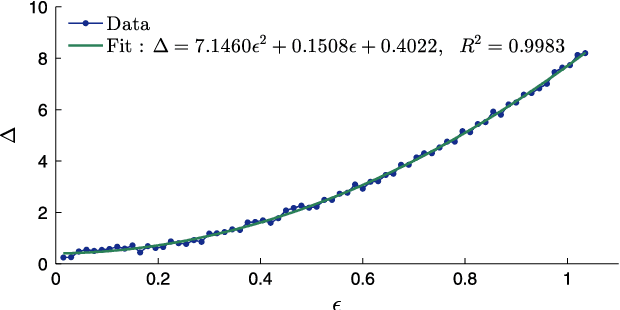
While the existence of low-dimensional embedding manifolds has been shown in patterns of collective motion, the current battery of nonlinear dimensionality reduction methods are not amenable to the analysis of such manifolds. This is mainly due to the necessary spectral decomposition step, which limits control over the mapping from the original high-dimensional space to the embedding space. Here, we propose an alternative approach that demands a two-dimensional embedding which topologically summarizes the high-dimensional data. In this sense, our approach is closely related to the construction of one-dimensional principal curves that minimize orthogonal error to data points subject to smoothness constraints. Specifically, we construct a two-dimensional principal manifold directly in the high-dimensional space using cubic smoothing splines, and define the embedding coordinates in terms of geodesic distances. Thus, the mapping from the high-dimensional data to the manifold is defined in terms of local coordinates. Through representative examples, we show that compared to existing nonlinear dimensionality reduction methods, the principal manifold retains the original structure even in noisy and sparse datasets. The principal manifold finding algorithm is applied to configurations obtained from a dynamical system of multiple agents simulating a complex maneuver called predator mobbing, and the resulting two-dimensional embedding is compared with that of a well-established nonlinear dimensionality reduction method.