Dimensionality Reduction of Collective Motion by Principal Manifolds

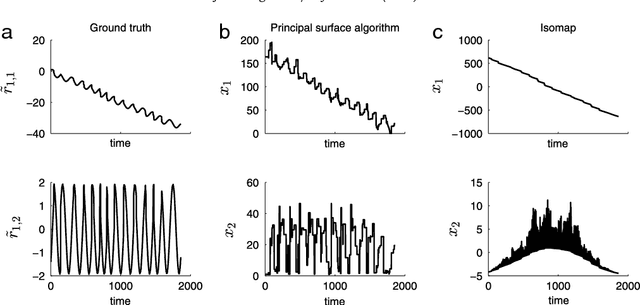
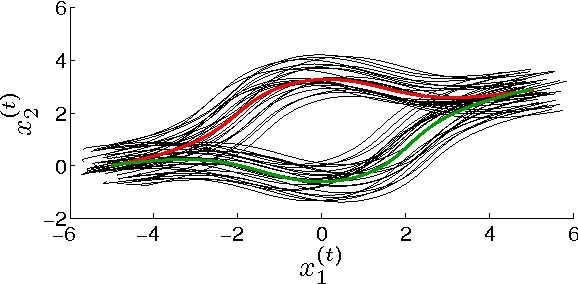
While the existence of low-dimensional embedding manifolds has been shown in patterns of collective motion, the current battery of nonlinear dimensionality reduction methods are not amenable to the analysis of such manifolds. This is mainly due to the necessary spectral decomposition step, which limits control over the mapping from the original high-dimensional space to the embedding space. Here, we propose an alternative approach that demands a two-dimensional embedding which topologically summarizes the high-dimensional data. In this sense, our approach is closely related to the construction of one-dimensional principal curves that minimize orthogonal error to data points subject to smoothness constraints. Specifically, we construct a two-dimensional principal manifold directly in the high-dimensional space using cubic smoothing splines, and define the embedding coordinates in terms of geodesic distances. Thus, the mapping from the high-dimensional data to the manifold is defined in terms of local coordinates. Through representative examples, we show that compared to existing nonlinear dimensionality reduction methods, the principal manifold retains the original structure even in noisy and sparse datasets. The principal manifold finding algorithm is applied to configurations obtained from a dynamical system of multiple agents simulating a complex maneuver called predator mobbing, and the resulting two-dimensional embedding is compared with that of a well-established nonlinear dimensionality reduction method.

Identifying manifolds underlying group motion in Vicsek agents

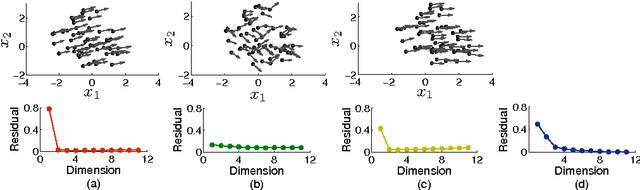
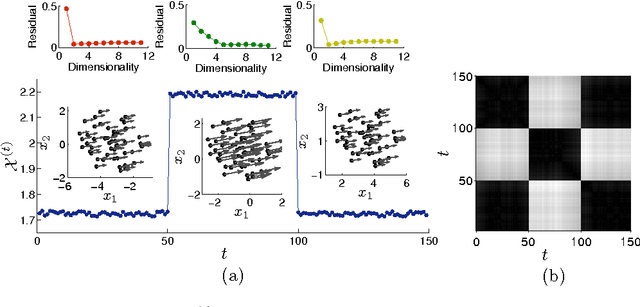
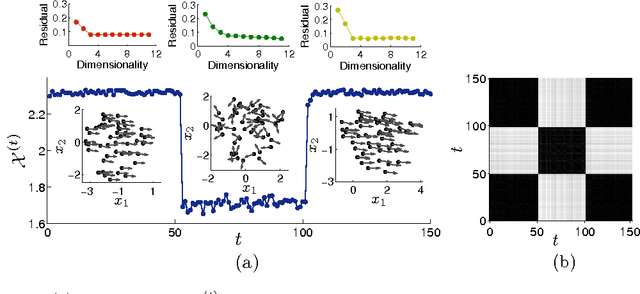
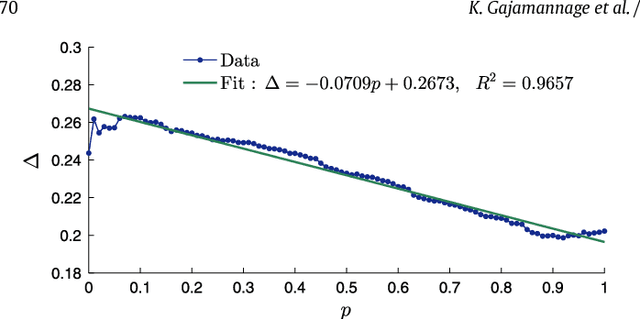
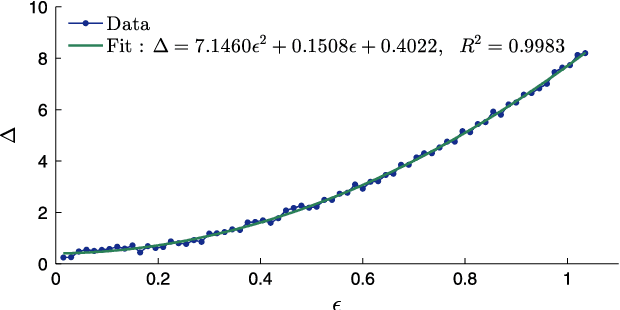
Collective motion of animal groups often undergoes changes due to perturbations. In a topological sense, we describe these changes as switching between low-dimensional embedding manifolds underlying a group of evolving agents. To characterize such manifolds, first we introduce a simple mapping of agents between time-steps. Then, we construct a novel metric which is susceptible to variations in the collective motion, thus revealing distinct underlying manifolds. The method is validated through three sample scenarios simulated using a Vicsek model, namely switching of speed, coordination, and structure of a group. Combined with a dimensionality reduction technique that is used to infer the dimensionality of the embedding manifold, this approach provides an effective model-free framework for the analysis of collective behavior across animal species.