Efficient and Robust Remote Sensing Image Denoising Using Randomized Approximation of Geodesics' Gramian on the Manifold Underlying the Patch Space

Remote sensing images are widely utilized in many disciplines such as feature recognition and scene semantic segmentation. However, due to environmental factors and the issues of the imaging system, the image quality is often degraded which may impair subsequent visual tasks. Even though denoising remote sensing images plays an essential role before applications, the current denoising algorithms fail to attain optimum performance since these images possess complex features in the texture. Denoising frameworks based on artificial neural networks have shown better performance; however, they require exhaustive training with heterogeneous samples that extensively consume resources like power, memory, computation, and latency. Thus, here we present a computationally efficient and robust remote sensing image denoising method that doesn't require additional training samples. This method partitions patches of a remote-sensing image in which a low-rank manifold, representing the noise-free version of the image, underlies the patch space. An efficient and robust approach to revealing this manifold is a randomized approximation of the singular value spectrum of the geodesics' Gramian matrix of the patch space. The method asserts a unique emphasis on each color channel during denoising so the three denoised channels are merged to produce the final image.

Recurrent Neural Networks for Dynamical Systems: Applications to Ordinary Differential Equations, Collective Motion, and Hydrological Modeling

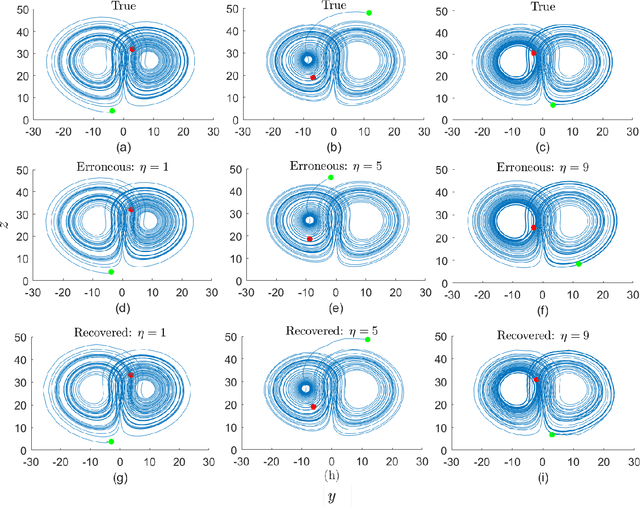
Classical methods of solving spatiotemporal dynamical systems include statistical approaches such as autoregressive integrated moving average, which assume linear and stationary relationships between systems' previous outputs. Development and implementation of linear methods are relatively simple, but they often do not capture non-linear relationships in the data. Thus, artificial neural networks (ANNs) are receiving attention from researchers in analyzing and forecasting dynamical systems. Recurrent neural networks (RNN), derived from feed-forward ANNs, use internal memory to process variable-length sequences of inputs. This allows RNNs to applicable for finding solutions for a vast variety of problems in spatiotemporal dynamical systems. Thus, in this paper, we utilize RNNs to treat some specific issues associated with dynamical systems. Specifically, we analyze the performance of RNNs applied to three tasks: reconstruction of correct Lorenz solutions for a system with a formulation error, reconstruction of corrupted collective motion trajectories, and forecasting of streamflow time series possessing spikes, representing three fields, namely, ordinary differential equations, collective motion, and hydrological modeling, respectively. We train and test RNNs uniquely in each task to demonstrate the broad applicability of RNNs in reconstruction and forecasting the dynamics of dynamical systems.