Federated learning model for predicting major postoperative complications

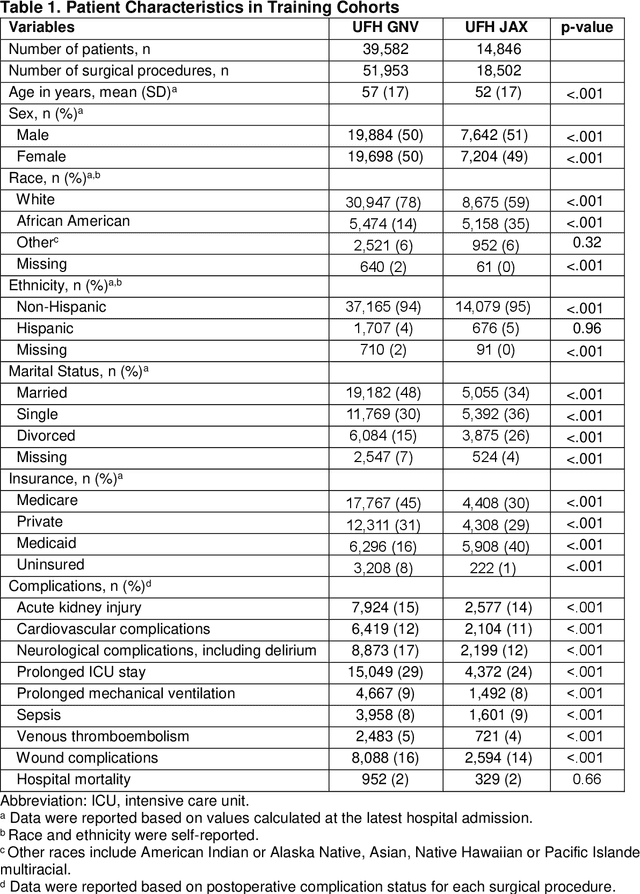
Background: The accurate prediction of postoperative complication risk using Electronic Health Records (EHR) and artificial intelligence shows great potential. Training a robust artificial intelligence model typically requires large-scale and diverse datasets. In reality, collecting medical data often encounters challenges surrounding privacy protection. Methods: This retrospective cohort study includes adult patients who were admitted to UFH Gainesville (GNV) (n = 79,850) and Jacksonville (JAX) (n = 28,636) for any type of inpatient surgical procedure. Using perioperative and intraoperative features, we developed federated learning models to predict nine major postoperative complications (i.e., prolonged intensive care unit stay and mechanical ventilation). We compared federated learning models with local learning models trained on a single site and central learning models trained on pooled dataset from two centers. Results: Our federated learning models achieved the area under the receiver operating characteristics curve (AUROC) values ranged from 0.81 for wound complications to 0.92 for prolonged ICU stay at UFH GNV center. At UFH JAX center, these values ranged from 0.73-0.74 for wound complications to 0.92-0.93 for hospital mortality. Federated learning models achieved comparable AUROC performance to central learning models, except for prolonged ICU stay, where the performance of federated learning models was slightly higher than central learning models at UFH GNV center, but slightly lower at UFH JAX center. In addition, our federated learning model obtained comparable performance to the best local learning model at each center, demonstrating strong generalizability. Conclusion: Federated learning is shown to be a useful tool to train robust and generalizable models from large scale data across multiple institutions where data protection barriers are high.

Efficient Noise Filtration of Images by Low-Rank Singular Vector Approximations of Geodesics' Gramian Matrix

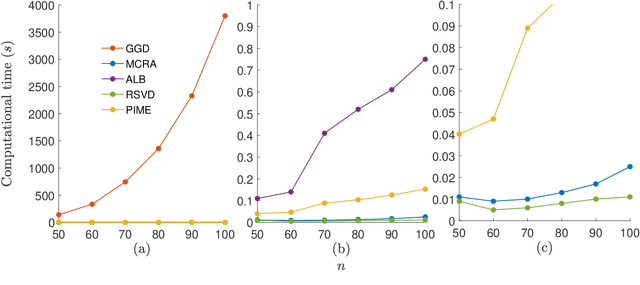
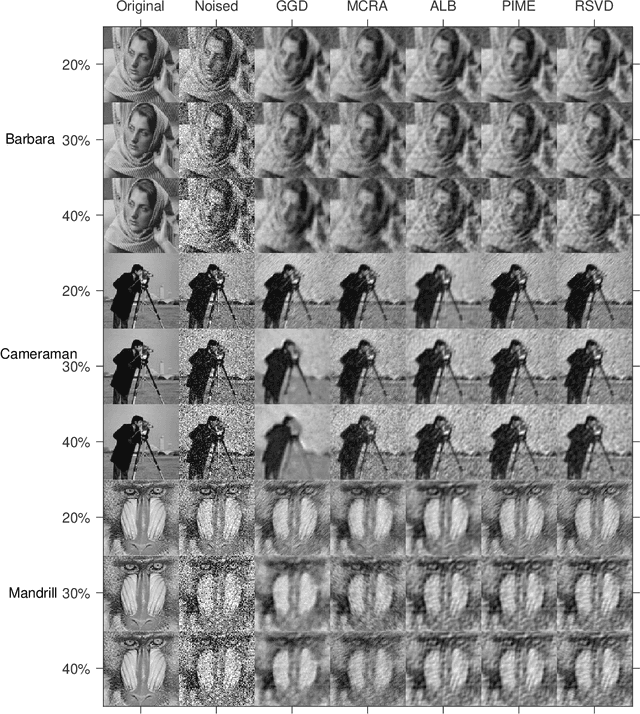
Modern society is interested in capturing high-resolution and fine-quality images due to the surge of sophisticated cameras. However, the noise contamination in the images not only inferior people's expectations but also conversely affects the subsequent processes if such images are utilized in computer vision tasks such as remote sensing, object tracking, etc. Even though noise filtration plays an essential role, real-time processing of a high-resolution image is limited by the hardware limitations of the image-capturing instruments. Geodesic Gramian Denoising (GGD) is a manifold-based noise filtering method that we introduced in our past research which utilizes a few prominent singular vectors of the geodesics' Gramian matrix for the noise filtering process. The applicability of GDD is limited as it encounters $\mathcal{O}(n^6)$ when denoising a given image of size $n\times n$ since GGD computes the prominent singular vectors of a $n^2 \times n^2$ data matrix that is implemented by singular value decomposition (SVD). In this research, we increase the efficiency of our GGD framework by replacing its SVD step with four diverse singular vector approximation techniques. Here, we compare both the computational time and the noise filtering performance between the four techniques integrated into GGD.

Real-time Forecasting of Time Series in Financial Markets Using Sequentially Trained Many-to-one LSTMs

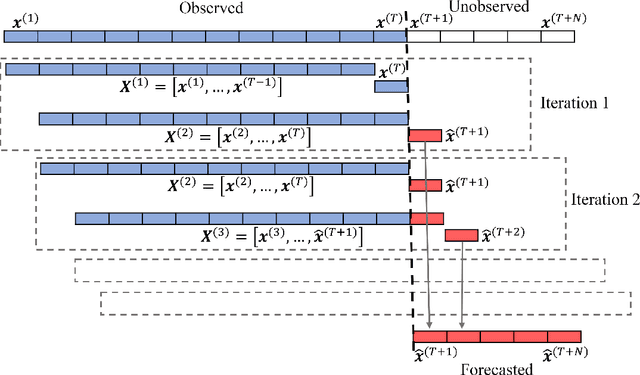
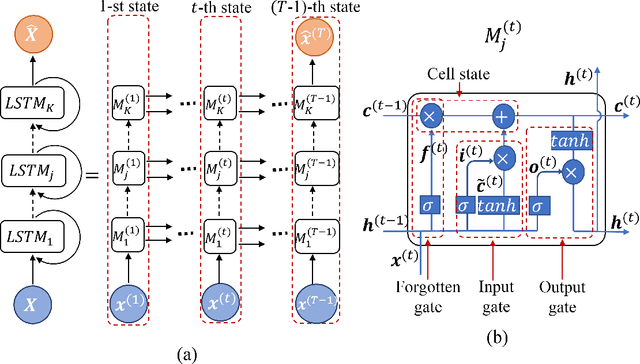
Financial markets are highly complex and volatile; thus, learning about such markets for the sake of making predictions is vital to make early alerts about crashes and subsequent recoveries. People have been using learning tools from diverse fields such as financial mathematics and machine learning in the attempt of making trustworthy predictions on such markets. However, the accuracy of such techniques had not been adequate until artificial neural network (ANN) frameworks were developed. Moreover, making accurate real-time predictions of financial time series is highly subjective to the ANN architecture in use and the procedure of training it. Long short-term memory (LSTM) is a member of the recurrent neural network family which has been widely utilized for time series predictions. Especially, we train two LSTMs with a known length, say $T$ time steps, of previous data and predict only one time step ahead. At each iteration, while one LSTM is employed to find the best number of epochs, the second LSTM is trained only for the best number of epochs to make predictions. We treat the current prediction as in the training set for the next prediction and train the same LSTM. While classic ways of training result in more error when the predictions are made further away in the test period, our approach is capable of maintaining a superior accuracy as training increases when it proceeds through the testing period. The forecasting accuracy of our approach is validated using three time series from each of the three diverse financial markets: stock, cryptocurrency, and commodity. The results are compared with those of an extended Kalman filter, an autoregressive model, and an autoregressive integrated moving average model.

Geodesic Gramian Denoising Applied to the Images Contaminated With Noise Sampled From Diverse Probability Distributions

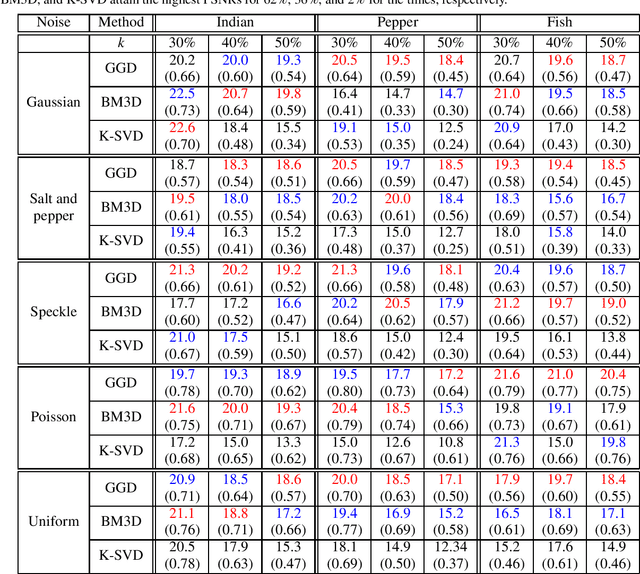
As quotidian use of sophisticated cameras surges, people in modern society are more interested in capturing fine-quality images. However, the quality of the images might be inferior to people's expectations due to the noise contamination in the images. Thus, filtering out the noise while preserving vital image features is an essential requirement. Current existing denoising methods have their own assumptions on the probability distribution in which the contaminated noise is sampled for the method to attain its expected denoising performance. In this paper, we utilize our recent Gramian-based filtering scheme to remove noise sampled from five prominent probability distributions from selected images. This method preserves image smoothness by adopting patches partitioned from the image, rather than pixels, and retains vital image features by performing denoising on the manifold underlying the patch space rather than in the image domain. We validate its denoising performance, using three benchmark computer vision test images applied to two state-of-the-art denoising methods, namely BM3D and K-SVD.

Recurrent Neural Networks for Dynamical Systems: Applications to Ordinary Differential Equations, Collective Motion, and Hydrological Modeling

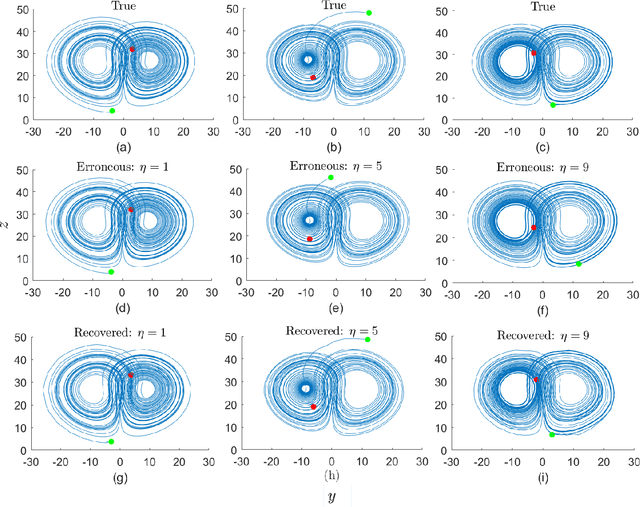
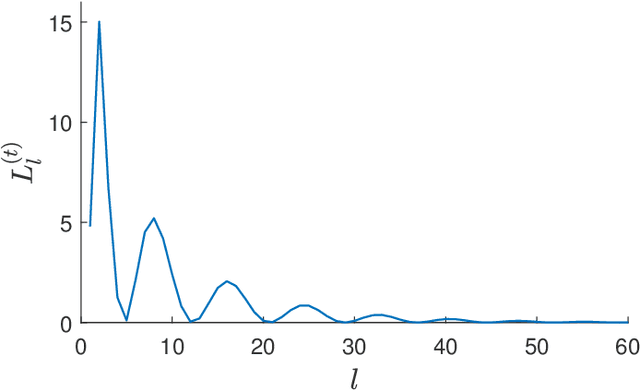
Classical methods of solving spatiotemporal dynamical systems include statistical approaches such as autoregressive integrated moving average, which assume linear and stationary relationships between systems' previous outputs. Development and implementation of linear methods are relatively simple, but they often do not capture non-linear relationships in the data. Thus, artificial neural networks (ANNs) are receiving attention from researchers in analyzing and forecasting dynamical systems. Recurrent neural networks (RNN), derived from feed-forward ANNs, use internal memory to process variable-length sequences of inputs. This allows RNNs to applicable for finding solutions for a vast variety of problems in spatiotemporal dynamical systems. Thus, in this paper, we utilize RNNs to treat some specific issues associated with dynamical systems. Specifically, we analyze the performance of RNNs applied to three tasks: reconstruction of correct Lorenz solutions for a system with a formulation error, reconstruction of corrupted collective motion trajectories, and forecasting of streamflow time series possessing spikes, representing three fields, namely, ordinary differential equations, collective motion, and hydrological modeling, respectively. We train and test RNNs uniquely in each task to demonstrate the broad applicability of RNNs in reconstruction and forecasting the dynamics of dynamical systems.

Reconstruction of Fragmented Trajectories of Collective Motion using Hadamard Deep Autoencoders

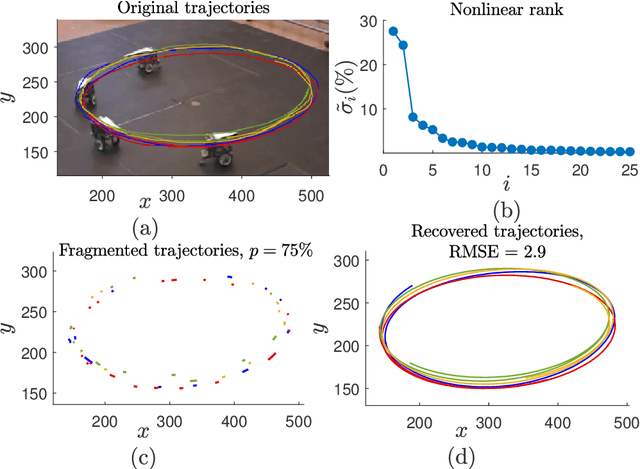
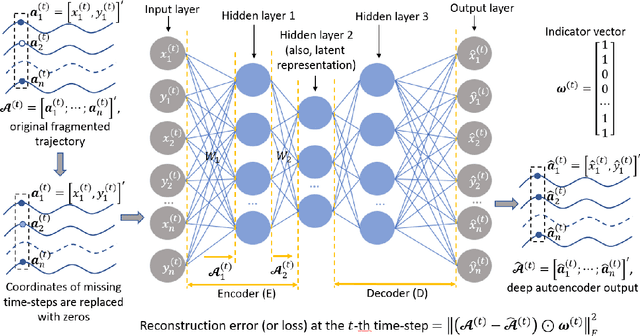
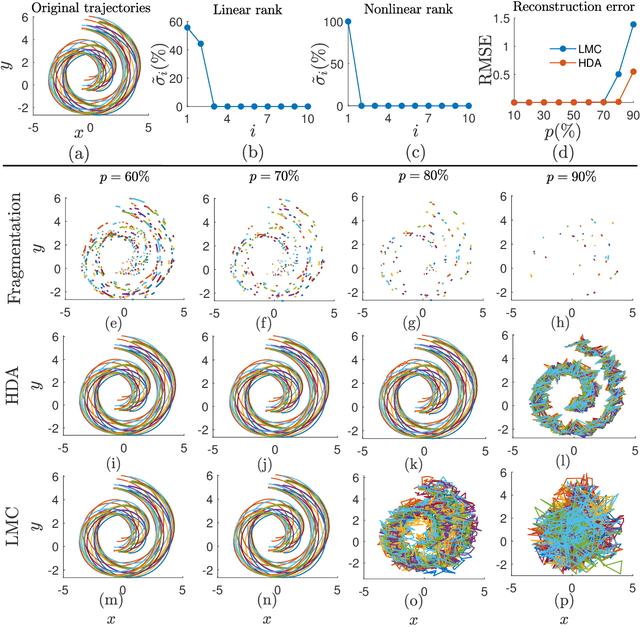
Learning dynamics of collectively moving agents such as fish or humans is an active field in research. Due to natural phenomena such as occlusion and change of illumination, the multi-object methods tracking such dynamics might lose track of the agents where that might result fragmentation in the constructed trajectories. Here, we present an extended deep autoencoder (DA) that we train only on fully observed segments of the trajectories by defining its loss function as the Hadamard product of a binary indicator matrix with the absolute difference between the outputs and the labels. The trajectories of the agents practicing collective motion is low-rank due to mutual interactions and dependencies between the agents that we utilize as the underlying pattern that our Hadamard deep autoencoder (HDA) codes during its training. The performance of our HDA is compared with that of a low-rank matrix completion scheme in the context of fragmented trajectory reconstruction.