Analysis of tidal flows through the Strait of Gibraltar using Dynamic Mode Decomposition

The Strait of Gibraltar is a region characterized by intricate oceanic sub-mesoscale features, influenced by topography, tidal forces, instabilities, and nonlinear hydraulic processes, all governed by the nonlinear equations of fluid motion. In this study, we aim to uncover the underlying physics of these phenomena within 3D MIT general circulation model simulations, including waves, eddies, and gyres. To achieve this, we employ Dynamic Mode Decomposition (DMD) to break down simulation snapshots into Koopman modes, with distinct exponential growth/decay rates and oscillation frequencies. Our objectives encompass evaluating DMD's efficacy in capturing known features, unveiling new elements, ranking modes, and exploring order reduction. We also introduce modifications to enhance DMD's robustness, numerical accuracy, and robustness of eigenvalues. DMD analysis yields a comprehensive understanding of flow patterns, internal wave formation, and the dynamics of the Strait of Gibraltar, its meandering behaviors, and the formation of a secondary gyre, notably the Western Alboran Gyre, as well as the propagation of Kelvin and coastal-trapped waves along the African coast. In doing so, it significantly advances our comprehension of intricate oceanographic phenomena and underscores the immense utility of DMD as an analytical tool for such complex datasets, suggesting that DMD could serve as a valuable addition to the toolkit of oceanographers.

Randomized Projection Learning Method forDynamic Mode Decomposition

A data-driven analysis method known as dynamic mode decomposition (DMD) approximates the linear Koopman operator on projected space. In the spirit of Johnson-Lindenstrauss Lemma, we will use random projection to estimate the DMD modes in reduced dimensional space. In practical applications, snapshots are in high dimensional observable space and the DMD operator matrix is massive. Hence, computing DMD with the full spectrum is infeasible, so our main computational goal is estimating the eigenvalue and eigenvectors of the DMD operator in a projected domain. We will generalize the current algorithm to estimate a projected DMD operator. We focus on a powerful and simple random projection algorithm that will reduce the computational and storage cost. While clearly, a random projection simplifies the algorithmic complexity of a detailed optimal projection, as we will show, generally the results can be excellent nonetheless, and quality understood through a well-developed theory of random projections. We will demonstrate that modes can be calculated for a low cost by the projected data with sufficient dimension. Keyword: Koopman Operator, Dynamic Mode Decomposition(DMD), Johnson-Lindenstrauss Lemma, Random Projection, Data-driven method.

On Geometry of Information Flow for Causal Inference

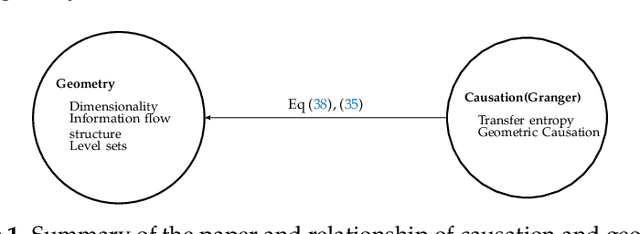
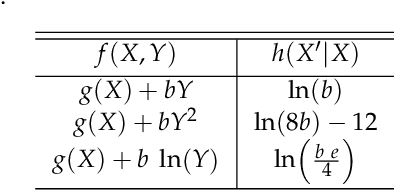
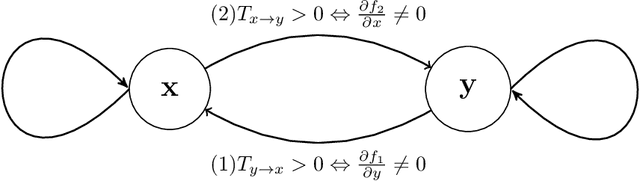
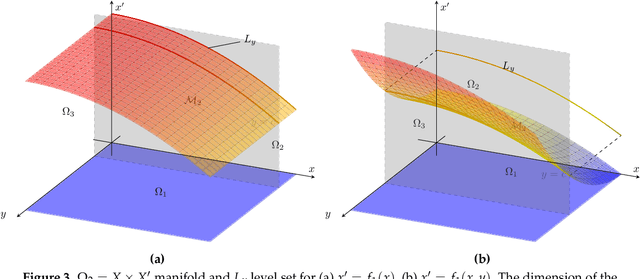
Causal inference is perhaps one of the most fundamental concepts in science, beginning originally from the works of some of the ancient philosophers, through today, but also weaved strongly in current work from statisticians, machine learning experts, and scientists from many other fields. This paper takes the perspective of information flow, which includes the Nobel prize winning work on Granger-causality, and the recently highly popular transfer entropy, these being probabilistic in nature. Our main contribution will be to develop analysis tools that will allow a geometric interpretation of information flow as a causal inference indicated by positive transfer entropy. We will describe the effective dimensionality of an underlying manifold as projected into the outcome space that summarizes information flow. Therefore contrasting the probabilistic and geometric perspectives, we will introduce a new measure of causal inference based on the fractal correlation dimension conditionally applied to competing explanations of future forecasts, which we will write $GeoC_{y\rightarrow x}$. This avoids some of the boundedness issues that we show exist for the transfer entropy, $T_{y\rightarrow x}$. We will highlight our discussions with data developed from synthetic models of successively more complex nature: then include the H\'{e}non map example, and finally a real physiological example relating breathing and heart rate function. Keywords: Causal Inference; Transfer Entropy; Differential Entropy; Correlation Dimension; Pinsker's Inequality; Frobenius-Perron operator.