ERFit: Entropic Regression Fit Matlab Package, for Data-Driven System Identification of Underlying Dynamic Equations

Data-driven sparse system identification becomes the general framework for a wide range of problems in science and engineering. It is a problem of growing importance in applied machine learning and artificial intelligence algorithms. In this work, we developed the Entropic Regression Software Package (ERFit), a MATLAB package for sparse system identification using the entropic regression method. The code requires minimal supervision, with a wide range of options that make it adapt easily to different problems in science and engineering. The ERFit is available at https://github.com/almomaa/ERFit-Package

Data-Driven Learning of Boolean Networks and Functions by Optimal Causation Entropy Principle

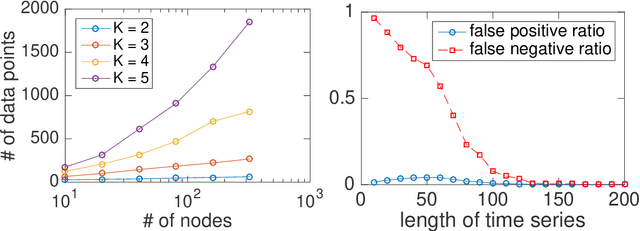
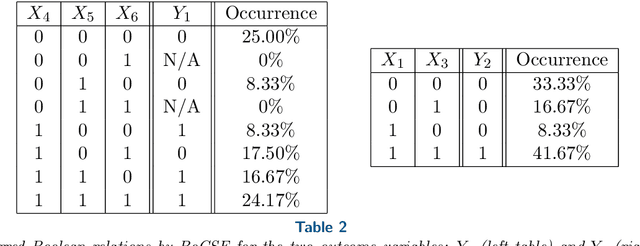
Boolean functions and networks are commonly used in the modeling and analysis of complex biological systems, and this paradigm is highly relevant in other important areas in data science and decision making, such as in the medical field and in the finance industry. Automated learning of a Boolean network and Boolean functions, from data, is a challenging task due in part to the large number of unknowns (including both the structure of the network and the functions) to be estimated, for which a brute force approach would be exponentially complex. In this paper we develop a new information theoretic methodology that we show to be significantly more efficient than previous approaches. Building on the recently developed optimal causation entropy principle (oCSE), that we proved can correctly infer networks distinguishing between direct versus indirect connections, we develop here an efficient algorithm that furthermore infers a Boolean network (including both its structure and function) based on data observed from the evolving states at nodes. We call this new inference method, Boolean optimal causation entropy (BoCSE), which we will show that our method is both computationally efficient and also resilient to noise. Furthermore, it allows for selection of a set of features that best explains the process, a statement that can be described as a networked Boolean function reduced order model. We highlight our method to the feature selection in several real-world examples: (1) diagnosis of urinary diseases, (2) Cardiac SPECT diagnosis, (3) informative positions in the game Tic-Tac-Toe, and (4) risk causality analysis of loans in default status. Our proposed method is effective and efficient in all examples.

An Early Warning Sign of Critical Transition in The Antarctic Ice Sheet. A New Data Driven Tool for Spatiotemporal Tipping Point

In this paper, we introduce a new tool for data-driven discovery of early warning signs of critical transitions in ice shelves, from remote sensing data. Our approach adopts principles of directed spectral clustering methodology considering an asymmetric affinity matrix and the associated directed graph Laplacian. We applied our approach generally to both reprocessed the ice velocity data, and also remote sensing satellite images of the Larsen C ice shelf. Our results allow us to (post-cast) predict fault lines responsible for the critical transitions leading to the break up of the Larsen C ice shelf crack, which resulted in the A68 iceberg, and we are able to do so, months earlier before the actual occurrence, and also much earlier than any other previously available methodology, in particular those based on interferometry.

Go With the Flow, on Jupiter and Snow. Coherence From Model-Free Video Data without Trajectories

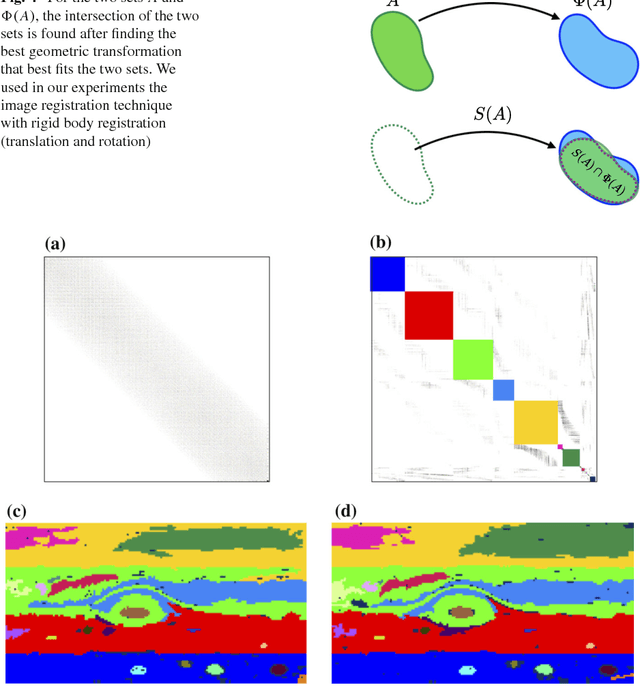
Viewing a data set such as the clouds of Jupiter, coherence is readily apparent to human observers, especially the Great Red Spot, but also other great storms and persistent structures. There are now many different definitions and perspectives mathematically describing coherent structures, but we will take an image processing perspective here. We describe an image processing perspective inference of coherent sets from a fluidic system directly from image data, without attempting to first model underlying flow fields, related to a concept in image processing called motion tracking. In contrast to standard spectral methods for image processing which are generally related to a symmetric affinity matrix, leading to standard spectral graph theory, we need a not symmetric affinity which arises naturally from the underlying arrow of time. We develop an anisotropic, directed diffusion operator corresponding to flow on a directed graph, from a directed affinity matrix developed with coherence in mind, and corresponding spectral graph theory from the graph Laplacian. Our methodology is not offered as more accurate than other traditional methods of finding coherent sets, but rather our approach works with alternative kinds of data sets, in the absence of vector field. Our examples will include partitioning the weather and cloud structures of Jupiter, and a local to Potsdam, N.Y. lake-effect snow event on Earth, as well as the benchmark test double-gyre system.