Uncertainty Quantification in Ensembles of Honest Regression Trees using Generalized Fiducial Inference

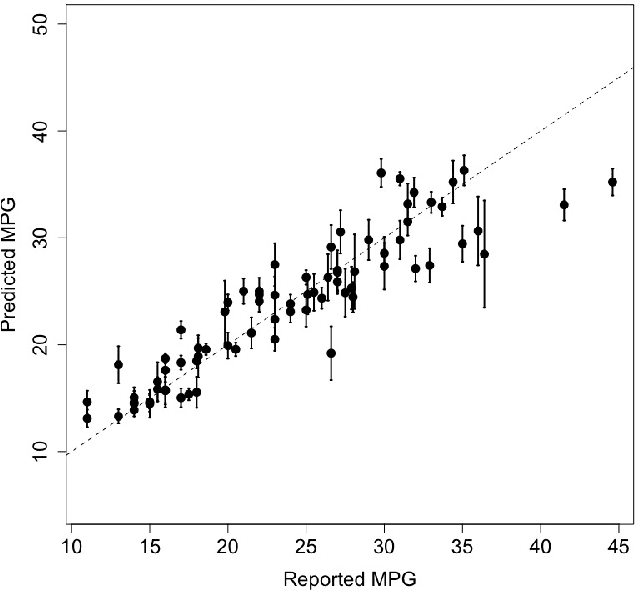
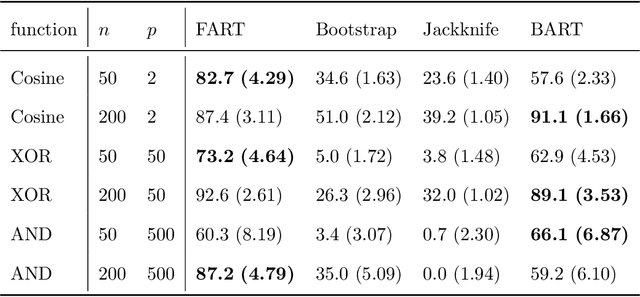
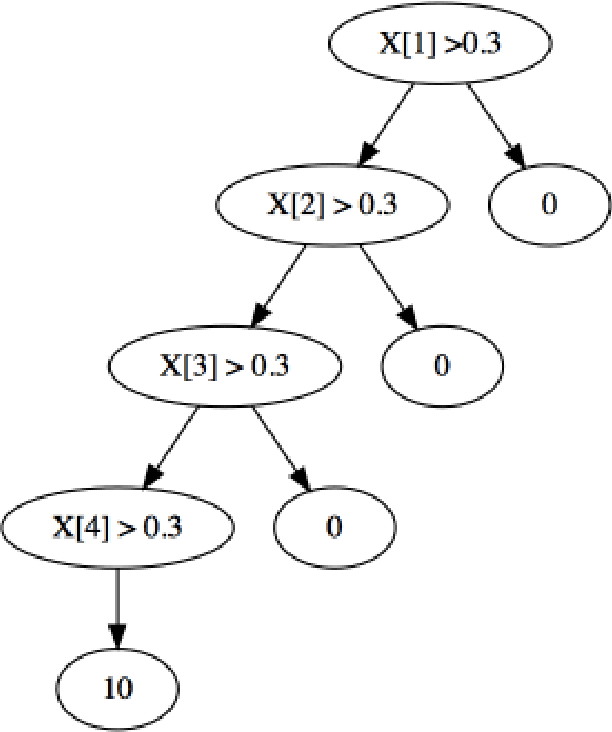
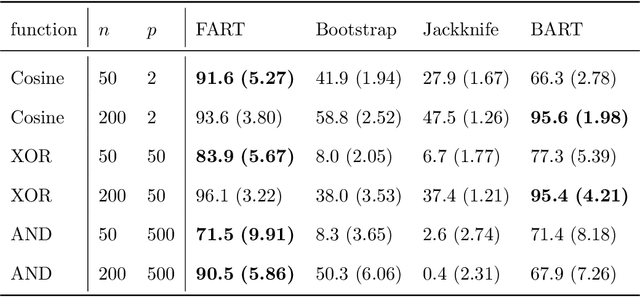
Due to their accuracies, methods based on ensembles of regression trees are a popular approach for making predictions. Some common examples include Bayesian additive regression trees, boosting and random forests. This paper focuses on honest random forests, which add honesty to the original form of random forests and are proved to have better statistical properties. The main contribution is a new method that quantifies the uncertainties of the estimates and predictions produced by honest random forests. The proposed method is based on the generalized fiducial methodology, and provides a fiducial density function that measures how likely each single honest tree is the true model. With such a density function, estimates and predictions, as well as their confidence/prediction intervals, can be obtained. The promising empirical properties of the proposed method are demonstrated by numerical comparisons with several state-of-the-art methods, and by applications to a few real data sets. Lastly, the proposed method is theoretically backed up by a strong asymptotic guarantee.

Measuring the Algorithmic Convergence of Randomized Ensembles: The Regression Setting

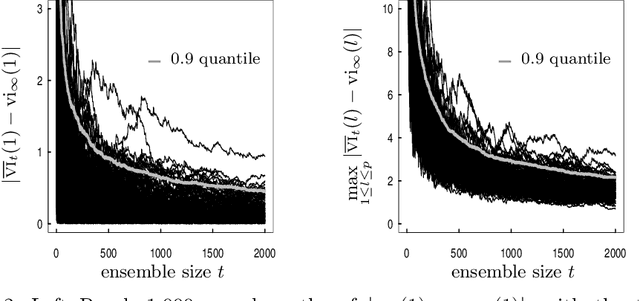
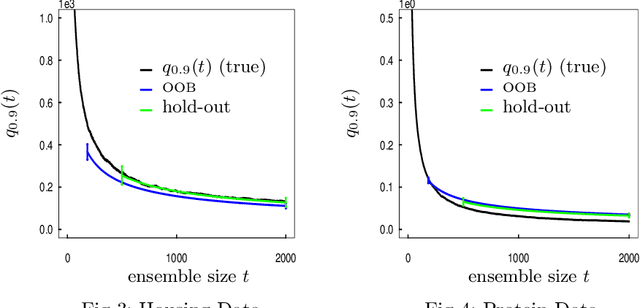
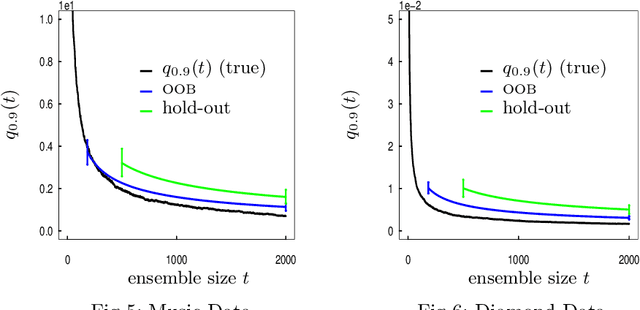
When randomized ensemble methods such as bagging and random forests are implemented, a basic question arises: Is the ensemble large enough? In particular, the practitioner desires a rigorous guarantee that a given ensemble will perform nearly as well as an ideal infinite ensemble (trained on the same data). The purpose of the current paper is to develop a bootstrap method for solving this problem in the context of regression --- which complements our companion paper in the context of classification (Lopes 2019). In contrast to the classification setting, the current paper shows that theoretical guarantees for the proposed bootstrap can be established under much weaker assumptions. In addition, we illustrate the flexibility of the method by showing how it can be adapted to measure algorithmic convergence for variable selection. Lastly, we provide numerical results demonstrating that the method works well in a range of situations.