Biased Dueling Bandits with Stochastic Delayed Feedback

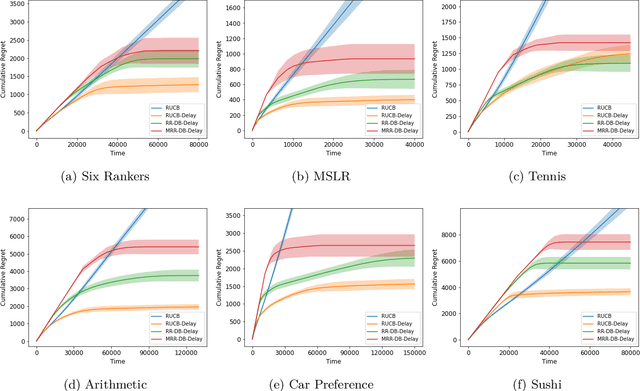
The dueling bandit problem, an essential variation of the traditional multi-armed bandit problem, has become significantly prominent recently due to its broad applications in online advertising, recommendation systems, information retrieval, and more. However, in many real-world applications, the feedback for actions is often subject to unavoidable delays and is not immediately available to the agent. This partially observable issue poses a significant challenge to existing dueling bandit literature, as it significantly affects how quickly and accurately the agent can update their policy on the fly. In this paper, we introduce and examine the biased dueling bandit problem with stochastic delayed feedback, revealing that this new practical problem will delve into a more realistic and intriguing scenario involving a preference bias between the selections. We present two algorithms designed to handle situations involving delay. Our first algorithm, requiring complete delay distribution information, achieves the optimal regret bound for the dueling bandit problem when there is no delay. The second algorithm is tailored for situations where the distribution is unknown, but only the expected value of delay is available. We provide a comprehensive regret analysis for the two proposed algorithms and then evaluate their empirical performance on both synthetic and real datasets.

Low-rank Matrix Bandits with Heavy-tailed Rewards

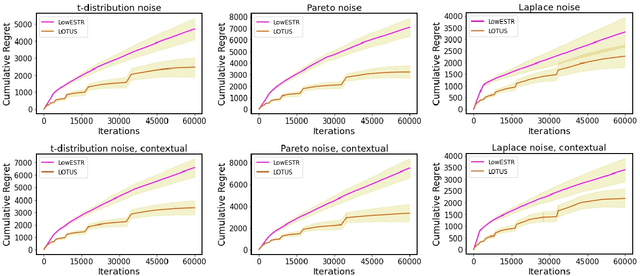
In stochastic low-rank matrix bandit, the expected reward of an arm is equal to the inner product between its feature matrix and some unknown $d_1$ by $d_2$ low-rank parameter matrix $\Theta^*$ with rank $r \ll d_1\wedge d_2$. While all prior studies assume the payoffs are mixed with sub-Gaussian noises, in this work we loosen this strict assumption and consider the new problem of \underline{low}-rank matrix bandit with \underline{h}eavy-\underline{t}ailed \underline{r}ewards (LowHTR), where the rewards only have finite $(1+\delta)$ moment for some $\delta \in (0,1]$. By utilizing the truncation on observed payoffs and the dynamic exploration, we propose a novel algorithm called LOTUS attaining the regret bound of order $\tilde O(d^\frac{3}{2}r^\frac{1}{2}T^\frac{1}{1+\delta}/\tilde{D}_{rr})$ without knowing $T$, which matches the state-of-the-art regret bound under sub-Gaussian noises~\citep{lu2021low,kang2022efficient} with $\delta = 1$. Moreover, we establish a lower bound of the order $\Omega(d^\frac{\delta}{1+\delta} r^\frac{\delta}{1+\delta} T^\frac{1}{1+\delta}) = \Omega(T^\frac{1}{1+\delta})$ for LowHTR, which indicates our LOTUS is nearly optimal in the order of $T$. In addition, we improve LOTUS so that it does not require knowledge of the rank $r$ with $\tilde O(dr^\frac{3}{2}T^\frac{1+\delta}{1+2\delta})$ regret bound, and it is efficient under the high-dimensional scenario. We also conduct simulations to demonstrate the practical superiority of our algorithm.

Efficient Frameworks for Generalized Low-Rank Matrix Bandit Problems

In the stochastic contextual low-rank matrix bandit problem, the expected reward of an action is given by the inner product between the action's feature matrix and some fixed, but initially unknown $d_1$ by $d_2$ matrix $\Theta^*$ with rank $r \ll \{d_1, d_2\}$, and an agent sequentially takes actions based on past experience to maximize the cumulative reward. In this paper, we study the generalized low-rank matrix bandit problem, which has been recently proposed in \cite{lu2021low} under the Generalized Linear Model (GLM) framework. To overcome the computational infeasibility and theoretical restrain of existing algorithms on this problem, we first propose the G-ESTT framework that modifies the idea from \cite{jun2019bilinear} by using Stein's method on the subspace estimation and then leverage the estimated subspaces via a regularization idea. Furthermore, we remarkably improve the efficiency of G-ESTT by using a novel exclusion idea on the estimated subspace instead, and propose the G-ESTS framework. We also show that G-ESTT can achieve the $\tilde{O}(\sqrt{(d_1+d_2)MrT})$ bound of regret while G-ESTS can achineve the $\tilde{O}(\sqrt{(d_1+d_2)^{3/2}Mr^{3/2}T})$ bound of regret under mild assumption up to logarithm terms, where $M$ is some problem dependent value. Under a reasonable assumption that $M = O((d_1+d_2)^2)$ in our problem setting, the regret of G-ESTT is consistent with the current best regret of $\tilde{O}((d_1+d_2)^{3/2} \sqrt{rT}/D_{rr})$~\citep{lu2021low} ($D_{rr}$ will be defined later). For completeness, we conduct experiments to illustrate that our proposed algorithms, especially G-ESTS, are also computationally tractable and consistently outperform other state-of-the-art (generalized) linear matrix bandit methods based on a suite of simulations.

Try with Simpler -- An Evaluation of Improved Principal Component Analysis in Log-based Anomaly Detection

The rapid growth of deep learning (DL) has spurred interest in enhancing log-based anomaly detection. This approach aims to extract meaning from log events (log message templates) and develop advanced DL models for anomaly detection. However, these DL methods face challenges like heavy reliance on training data, labels, and computational resources due to model complexity. In contrast, traditional machine learning and data mining techniques are less data-dependent and more efficient but less effective than DL. To make log-based anomaly detection more practical, the goal is to enhance traditional techniques to match DL's effectiveness. Previous research in a different domain (linking questions on Stack Overflow) suggests that optimized traditional techniques can rival state-of-the-art DL methods. Drawing inspiration from this concept, we conducted an empirical study. We optimized the unsupervised PCA (Principal Component Analysis), a traditional technique, by incorporating lightweight semantic-based log representation. This addresses the issue of unseen log events in training data, enhancing log representation. Our study compared seven log-based anomaly detection methods, including four DL-based, two traditional, and the optimized PCA technique, using public and industrial datasets. Results indicate that the optimized unsupervised PCA technique achieves similar effectiveness to advanced supervised/semi-supervised DL methods while being more stable with limited training data and resource-efficient. This demonstrates the adaptability and strength of traditional techniques through small yet impactful adaptations.

Robust Lipschitz Bandits to Adversarial Corruptions

Lipschitz bandit is a variant of stochastic bandits that deals with a continuous arm set defined on a metric space, where the reward function is subject to a Lipschitz constraint. In this paper, we introduce a new problem of Lipschitz bandits in the presence of adversarial corruptions where an adaptive adversary corrupts the stochastic rewards up to a total budget $C$. The budget is measured by the sum of corruption levels across the time horizon $T$. We consider both weak and strong adversaries, where the weak adversary is unaware of the current action before the attack, while the strong one can observe it. Our work presents the first line of robust Lipschitz bandit algorithms that can achieve sub-linear regret under both types of adversary, even when the total budget of corruption $C$ is unrevealed to the agent. We provide a lower bound under each type of adversary, and show that our algorithm is optimal under the strong case. Finally, we conduct experiments to illustrate the effectiveness of our algorithms against two classic kinds of attacks.

Online Continuous Hyperparameter Optimization for Contextual Bandits

In stochastic contextual bandit problems, an agent sequentially makes actions from a time-dependent action set based on past experience to minimize the cumulative regret. Like many other machine learning algorithms, the performance of bandits heavily depends on their multiple hyperparameters, and theoretically derived parameter values may lead to unsatisfactory results in practice. Moreover, it is infeasible to use offline tuning methods like cross validation to choose hyperparameters under the bandit environment, as the decisions should be made in real time. To address this challenge, we propose the first online continuous hyperparameter tuning framework for contextual bandits to learn the optimal parameter configuration within a search space on the fly. Specifically, we use a double-layer bandit framework named CDT (Continuous Dynamic Tuning) and formulate the hyperparameter optimization as a non-stationary continuum-armed bandit, where each arm represents a combination of hyperparameters, and the corresponding reward is the algorithmic result. For the top layer, we propose the Zooming TS algorithm that utilizes Thompson Sampling (TS) for exploration and a restart technique to get around the switching environment. The proposed CDT framework can be easily used to tune contextual bandit algorithms without any pre-specified candidate set for hyperparameters. We further show that it could achieve sublinear regret in theory and performs consistently better on both synthetic and real datasets in practice.

Adapting Stepsizes by Momentumized Gradients Improves Optimization and Generalization

Adaptive gradient methods, such as \textsc{Adam}, have achieved tremendous success in machine learning. Scaling gradients by square roots of the running averages of squared past gradients, such methods are able to attain rapid training of modern deep neural networks. Nevertheless, they are observed to generalize worse than stochastic gradient descent (\textsc{SGD}) and tend to be trapped in local minima at an early stage during training. Intriguingly, we discover that substituting the gradient in the preconditioner term with the momentumized version in \textsc{Adam} can well solve the issues. The intuition is that gradient with momentum contains more accurate directional information and therefore its second moment estimation is a better choice for scaling than raw gradient's. Thereby we propose \textsc{AdaMomentum} as a new optimizer reaching the goal of training faster while generalizing better. We further develop a theory to back up the improvement in optimization and generalization and provide convergence guarantee under both convex and nonconvex settings. Extensive experiments on various models and tasks demonstrate that \textsc{AdaMomentum} exhibits comparable performance to \textsc{SGD} on vision tasks, and achieves state-of-the-art results consistently on other tasks including language processing.

Sequence-based deep learning antibody design for in silico antibody affinity maturation

Antibody therapeutics has been extensively studied in drug discovery and development within the past decades. One increasingly popular focus in the antibody discovery pipeline is the optimization step for therapeutic leads. Both traditional methods and in silico approaches aim to generate candidates with high binding affinity against specific target antigens. Traditional in vitro approaches use hybridoma or phage display for candidate selection, and surface plasmon resonance (SPR) for evaluation, while in silico computational approaches aim to reduce the high cost and improve efficiency by incorporating mathematical algorithms and computational processing power in the design process. In the present study, we investigated different graph-based designs for depicting antibody-antigen interactions in terms of antibody affinity prediction using deep learning techniques. While other in silico computations require experimentally determined crystal structures, our study took interest in the capability of sequence-based models for in silico antibody maturation. Our preliminary studies achieved satisfying prediction accuracy on binding affinities comparing to conventional approaches and other deep learning approaches. To further study the antibody-antigen binding specificity, and to simulate the optimization process in real-world scenario, we introduced pairwise prediction strategy. We performed analysis based on both baseline and pairwise prediction results. The resulting prediction and efficiency prove the feasibility and computational efficiency of sequence-based method to be adapted as a scalable industry practice.