TART: Boosting Clean Accuracy Through Tangent Direction Guided Adversarial Training

Adversarial training has been shown to be successful in enhancing the robustness of deep neural networks against adversarial attacks. However, this robustness is accompanied by a significant decline in accuracy on clean data. In this paper, we propose a novel method, called Tangent Direction Guided Adversarial Training (TART), that leverages the tangent space of the data manifold to ameliorate the existing adversarial defense algorithms. We argue that training with adversarial examples having large normal components significantly alters the decision boundary and hurts accuracy. TART mitigates this issue by estimating the tangent direction of adversarial examples and allocating an adaptive perturbation limit according to the norm of their tangential component. To the best of our knowledge, our paper is the first work to consider the concept of tangent space and direction in the context of adversarial defense. We validate the effectiveness of TART through extensive experiments on both simulated and benchmark datasets. The results demonstrate that TART consistently boosts clean accuracy while retaining a high level of robustness against adversarial attacks. Our findings suggest that incorporating the geometric properties of data can lead to more effective and efficient adversarial training methods.

Biased Dueling Bandits with Stochastic Delayed Feedback

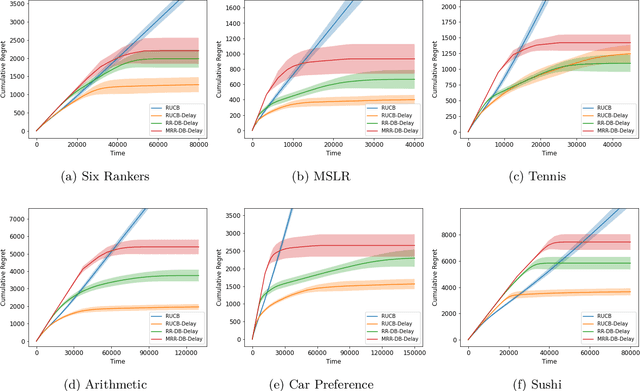
The dueling bandit problem, an essential variation of the traditional multi-armed bandit problem, has become significantly prominent recently due to its broad applications in online advertising, recommendation systems, information retrieval, and more. However, in many real-world applications, the feedback for actions is often subject to unavoidable delays and is not immediately available to the agent. This partially observable issue poses a significant challenge to existing dueling bandit literature, as it significantly affects how quickly and accurately the agent can update their policy on the fly. In this paper, we introduce and examine the biased dueling bandit problem with stochastic delayed feedback, revealing that this new practical problem will delve into a more realistic and intriguing scenario involving a preference bias between the selections. We present two algorithms designed to handle situations involving delay. Our first algorithm, requiring complete delay distribution information, achieves the optimal regret bound for the dueling bandit problem when there is no delay. The second algorithm is tailored for situations where the distribution is unknown, but only the expected value of delay is available. We provide a comprehensive regret analysis for the two proposed algorithms and then evaluate their empirical performance on both synthetic and real datasets.

ALASCA: Rethinking Label Smoothing for Deep Learning Under Label Noise

As label noise, one of the most popular distribution shifts, severely degrades deep neural networks' generalization performance, robust training with noisy labels is becoming an important task in modern deep learning. In this paper, we propose our framework, coined as Adaptive LAbel smoothing on Sub-ClAssifier (ALASCA), that provides a robust feature extractor with theoretical guarantee and negligible additional computation. First, we derive that the label smoothing (LS) incurs implicit Lipschitz regularization (LR). Furthermore, based on these derivations, we apply the adaptive LS (ALS) on sub-classifiers architectures for the practical application of adaptive LR on intermediate layers. We conduct extensive experiments for ALASCA and combine it with previous noise-robust methods on several datasets and show our framework consistently outperforms corresponding baselines.

Graph Optimal Transport with Transition Couplings of Random Walks

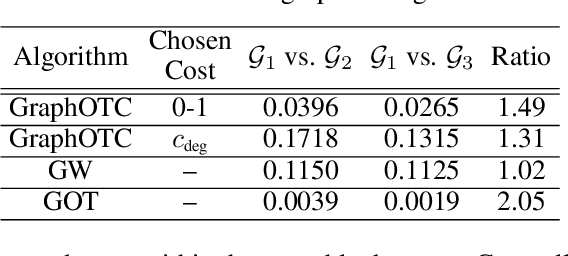
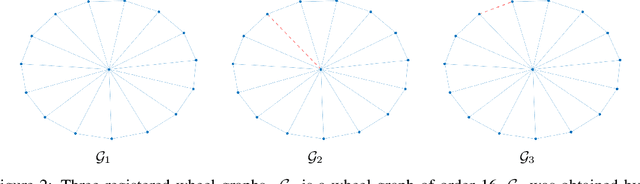
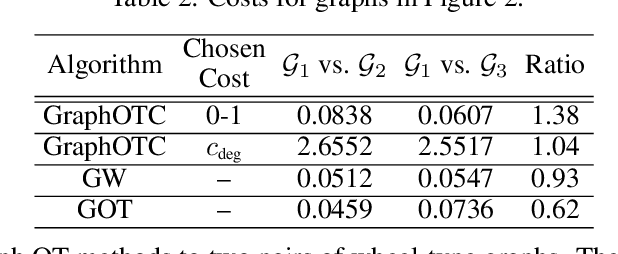
We present a novel approach to optimal transport between graphs from the perspective of stationary Markov chains. A weighted graph may be associated with a stationary Markov chain by means of a random walk on the vertex set with transition distributions depending on the edge weights of the graph. After drawing this connection, we describe how optimal transport techniques for stationary Markov chains may be used in order to perform comparison and alignment of the graphs under study. In particular, we propose the graph optimal transition coupling problem, referred to as GraphOTC, in which the Markov chains associated to two given graphs are optimally synchronized to minimize an expected cost. The joint synchronized chain yields an alignment of the vertices and edges in the two graphs, and the expected cost of the synchronized chain acts as a measure of distance or dissimilarity between the two graphs. We demonstrate that GraphOTC performs equal to or better than existing state-of-the-art techniques in graph optimal transport for several tasks and datasets. Finally, we also describe a generalization of the GraphOTC problem, called the FusedOTC problem, from which we recover the GraphOTC and OT costs as special cases.