TART: Boosting Clean Accuracy Through Tangent Direction Guided Adversarial Training

Adversarial training has been shown to be successful in enhancing the robustness of deep neural networks against adversarial attacks. However, this robustness is accompanied by a significant decline in accuracy on clean data. In this paper, we propose a novel method, called Tangent Direction Guided Adversarial Training (TART), that leverages the tangent space of the data manifold to ameliorate the existing adversarial defense algorithms. We argue that training with adversarial examples having large normal components significantly alters the decision boundary and hurts accuracy. TART mitigates this issue by estimating the tangent direction of adversarial examples and allocating an adaptive perturbation limit according to the norm of their tangential component. To the best of our knowledge, our paper is the first work to consider the concept of tangent space and direction in the context of adversarial defense. We validate the effectiveness of TART through extensive experiments on both simulated and benchmark datasets. The results demonstrate that TART consistently boosts clean accuracy while retaining a high level of robustness against adversarial attacks. Our findings suggest that incorporating the geometric properties of data can lead to more effective and efficient adversarial training methods.

Unsupervised Solution Operator Learning for Mean-Field Games via Sampling-Invariant Parametrizations

Recent advances in deep learning has witnessed many innovative frameworks that solve high dimensional mean-field games (MFG) accurately and efficiently. These methods, however, are restricted to solving single-instance MFG and demands extensive computational time per instance, limiting practicality. To overcome this, we develop a novel framework to learn the MFG solution operator. Our model takes a MFG instances as input and output their solutions with one forward pass. To ensure the proposed parametrization is well-suited for operator learning, we introduce and prove the notion of sampling invariance for our model, establishing its convergence to a continuous operator in the sampling limit. Our method features two key advantages. First, it is discretization-free, making it particularly suitable for learning operators of high-dimensional MFGs. Secondly, it can be trained without the need for access to supervised labels, significantly reducing the computational overhead associated with creating training datasets in existing operator learning methods. We test our framework on synthetic and realistic datasets with varying complexity and dimensionality to substantiate its robustness.

Emulating Complex Synapses Using Interlinked Proton Conductors

In terms of energy efficiency and computational speed, neuromorphic electronics based on non-volatile memory devices is expected to be one of most promising hardware candidates for future artificial intelligence (AI). However, catastrophic forgetting, networks rapidly overwriting previously learned weights when learning new tasks, remains as a pivotal hurdle in either digital or analog AI chips for unleashing the true power of brain-like computing. To address catastrophic forgetting in the context of online memory storage, a complex synapse model (the Benna-Fusi model) has been proposed recently[1], whose synaptic weight and internal variables evolve following a diffusion dynamics. In this work, by designing a proton transistor with a series of charge-diffusion-controlled storage components, we have experimentally realized the Benna-Fusi artificial complex synapse. The memory consolidation from coupled storage components is revealed by both numerical simulations and experimental observations. Different memory timescales for the complex synapse are engineered by the diffusion length of charge carriers, the capacity and number of coupled storage components. The advantage of the demonstrated complex synapse in both memory capacity and memory consolidation is revealed by neural network simulations of face familiarity detection. Our experimental realization of the complex synapse suggests a promising approach to enhance memory capacity and to enable continual learning.

Generalization Error Guaranteed Auto-Encoder-Based Nonlinear Model Reduction for Operator Learning

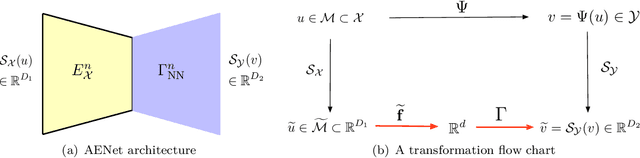
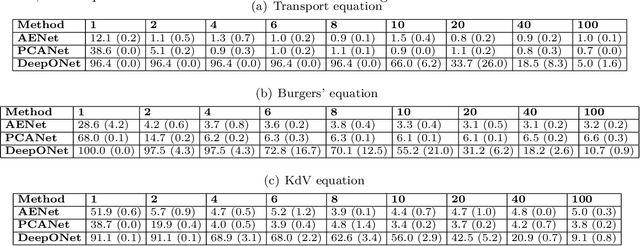
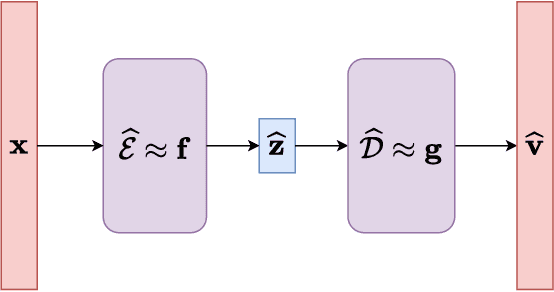
Many physical processes in science and engineering are naturally represented by operators between infinite-dimensional function spaces. The problem of operator learning, in this context, seeks to extract these physical processes from empirical data, which is challenging due to the infinite or high dimensionality of data. An integral component in addressing this challenge is model reduction, which reduces both the data dimensionality and problem size. In this paper, we utilize low-dimensional nonlinear structures in model reduction by investigating Auto-Encoder-based Neural Network (AENet). AENet first learns the latent variables of the input data and then learns the transformation from these latent variables to corresponding output data. Our numerical experiments validate the ability of AENet to accurately learn the solution operator of nonlinear partial differential equations. Furthermore, we establish a mathematical and statistical estimation theory that analyzes the generalization error of AENet. Our theoretical framework shows that the sample complexity of training AENet is intricately tied to the intrinsic dimension of the modeled process, while also demonstrating the remarkable resilience of AENet to noise.

Deep Nonparametric Estimation of Intrinsic Data Structures by Chart Autoencoders: Generalization Error and Robustness

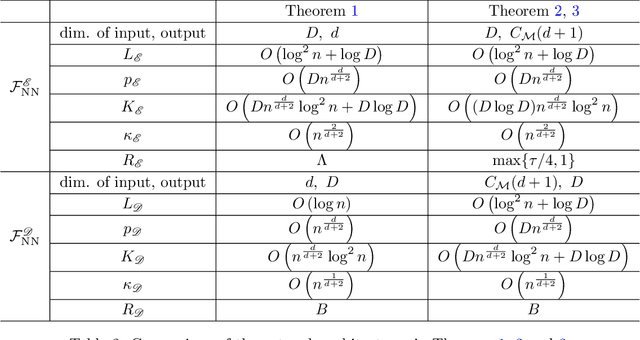
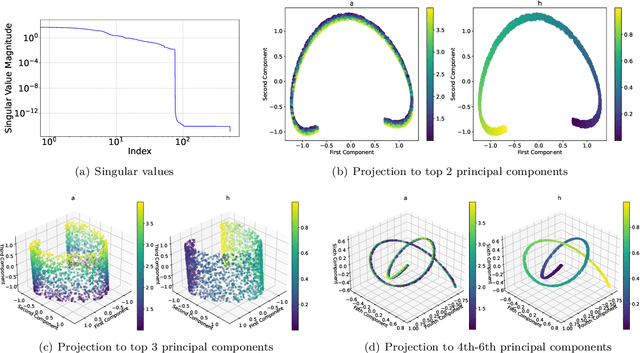
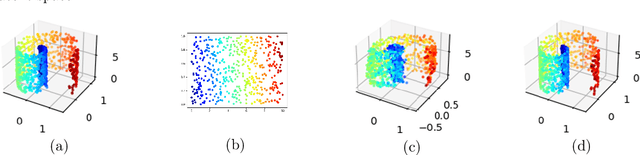
Autoencoders have demonstrated remarkable success in learning low-dimensional latent features of high-dimensional data across various applications. Assuming that data are sampled near a low-dimensional manifold, we employ chart autoencoders, which encode data into low-dimensional latent features on a collection of charts, preserving the topology and geometry of the data manifold. Our paper establishes statistical guarantees on the generalization error of chart autoencoders, and we demonstrate their denoising capabilities by considering $n$ noisy training samples, along with their noise-free counterparts, on a $d$-dimensional manifold. By training autoencoders, we show that chart autoencoders can effectively denoise the input data with normal noise. We prove that, under proper network architectures, chart autoencoders achieve a squared generalization error in the order of $\displaystyle n^{-\frac{2}{d+2}}\log^4 n$, which depends on the intrinsic dimension of the manifold and only weakly depends on the ambient dimension and noise level. We further extend our theory on data with noise containing both normal and tangential components, where chart autoencoders still exhibit a denoising effect for the normal component. As a special case, our theory also applies to classical autoencoders, as long as the data manifold has a global parametrization. Our results provide a solid theoretical foundation for the effectiveness of autoencoders, which is further validated through several numerical experiments.

Semi-Supervised Manifold Learning with Complexity Decoupled Chart Autoencoders

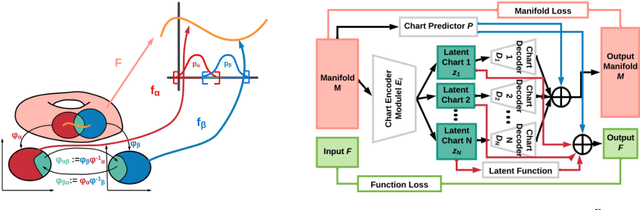
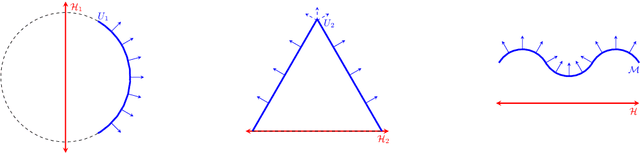
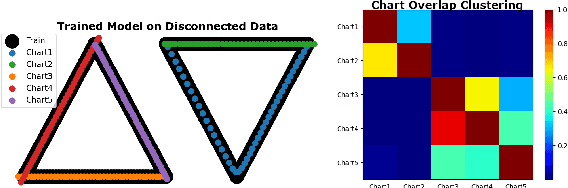
Autoencoding is a popular method in representation learning. Conventional autoencoders employ symmetric encoding-decoding procedures and a simple Euclidean latent space to detect hidden low-dimensional structures in an unsupervised way. This work introduces a chart autoencoder with an asymmetric encoding-decoding process that can incorporate additional semi-supervised information such as class labels. Besides enhancing the capability for handling data with complicated topological and geometric structures, these models can successfully differentiate nearby but disjoint manifolds and intersecting manifolds with only a small amount of supervision. Moreover, this model only requires a low complexity encoder, such as local linear projection. We discuss the theoretical approximation power of such networks that essentially depends on the intrinsic dimension of the data manifold and not the dimension of the observations. Our numerical experiments on synthetic and real-world data verify that the proposed model can effectively manage data with multi-class nearby but disjoint manifolds of different classes, overlapping manifolds, and manifolds with non-trivial topology.

Bridging Mean-Field Games and Normalizing Flows with Trajectory Regularization

Mean-field games (MFGs) are a modeling framework for systems with a large number of interacting agents. They have applications in economics, finance, and game theory. Normalizing flows (NFs) are a family of deep generative models that compute data likelihoods by using an invertible mapping, which is typically parameterized by using neural networks. They are useful for density modeling and data generation. While active research has been conducted on both models, few noted the relationship between the two. In this work, we unravel the connections between MFGs and NFs by contextualizing the training of an NF as solving the MFG. This is achieved by reformulating the MFG problem in terms of agent trajectories and parameterizing a discretization of the resulting MFG with flow architectures. With this connection, we explore two research directions. First, we employ expressive NF architectures to accurately solve high-dimensional MFGs, sidestepping the curse of dimensionality in traditional numerical methods. Compared with other deep learning approaches, our trajectory-based formulation encodes the continuity equation in the neural network, resulting in a better approximation of the population dynamics. Second, we regularize the training of NFs with transport costs and show the effectiveness on controlling the model's Lipschitz bound, resulting in better generalization performance. We demonstrate numerical results through comprehensive experiments on a variety of synthetic and real-life datasets.

Learning Geometrically Disentangled Representations of Protein Folding Simulations

Massive molecular simulations of drug-target proteins have been used as a tool to understand disease mechanism and develop therapeutics. This work focuses on learning a generative neural network on a structural ensemble of a drug-target protein, e.g. SARS-CoV-2 Spike protein, obtained from computationally expensive molecular simulations. Model tasks involve characterizing the distinct structural fluctuations of the protein bound to various drug molecules, as well as efficient generation of protein conformations that can serve as an complement of a molecular simulation engine. Specifically, we present a geometric autoencoder framework to learn separate latent space encodings of the intrinsic and extrinsic geometries of the protein structure. For this purpose, the proposed Protein Geometric AutoEncoder (ProGAE) model is trained on the protein contact map and the orientation of the backbone bonds of the protein. Using ProGAE latent embeddings, we reconstruct and generate the conformational ensemble of a protein at or near the experimental resolution, while gaining better interpretability and controllability in term of protein structure generation from the learned latent space. Additionally, ProGAE models are transferable to a different state of the same protein or to a new protein of different size, where only the dense layer decoding from the latent representation needs to be retrained. Results show that our geometric learning-based method enjoys both accuracy and efficiency for generating complex structural variations, charting the path toward scalable and improved approaches for analyzing and enhancing high-cost simulations of drug-target proteins.

Manifoldron: Direct Space Partition via Manifold Discovery

A neural network with the widely-used ReLU activation has been shown to partition the sample space into many convex polytopes for prediction. However, the parameterized way a neural network and other machine learning models use to partition the space has imperfections, e.g., the compromised interpretability for complex models, the inflexibility in decision boundary construction due to the generic character of the model, and the risk of being trapped into shortcut solutions. In contrast, although the non-parameterized models can adorably avoid or downplay these issues, they are usually insufficiently powerful either due to over-simplification or the failure to accommodate the manifold structures of data. In this context, we first propose a new type of machine learning models referred to as Manifoldron that directly derives decision boundaries from data and partitions the space via manifold structure discovery. Then, we systematically analyze the key characteristics of the Manifoldron including interpretability, manifold characterization capability, and its link to neural networks. The experimental results on 9 small and 11 large datasets demonstrate that the proposed Manifoldron performs competitively compared to the mainstream machine learning models. We have shared our code https://github.com/wdayang/Manifoldron for free download and evaluation.

Expressivity and Trainability of Quadratic Networks

Inspired by diversity of biological neurons, quadratic artificial neurons can play an important role in deep learning models. The type of quadratic neurons of our interest replaces the inner-product operation in the conventional neuron with a quadratic function. Despite promising results so far achieved by networks of quadratic neurons, there are important issues not well addressed. Theoretically, the superior expressivity of a quadratic network over either a conventional network or a conventional network via quadratic activation is not fully elucidated, which makes the use of quadratic networks not well grounded. Practically, although a quadratic network can be trained via generic backpropagation, it can be subject to a higher risk of collapse than the conventional counterpart. To address these issues, we first apply the spline theory and a measure from algebraic geometry to give two theorems that demonstrate better model expressivity of a quadratic network than the conventional counterpart with or without quadratic activation. Then, we propose an effective and efficient training strategy referred to as ReLinear to stabilize the training process of a quadratic network, thereby unleashing the full potential in its associated machine learning tasks. Comprehensive experiments on popular datasets are performed to support our findings and evaluate the performance of quadratic deep learning.