Generalization Error Guaranteed Auto-Encoder-Based Nonlinear Model Reduction for Operator Learning
Paper and Code
Jan 19, 2024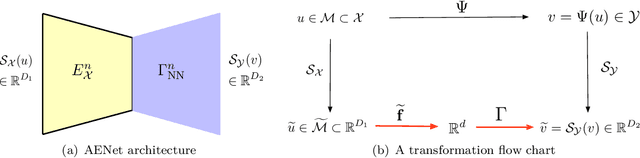
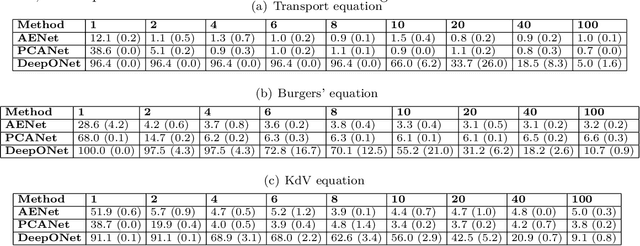
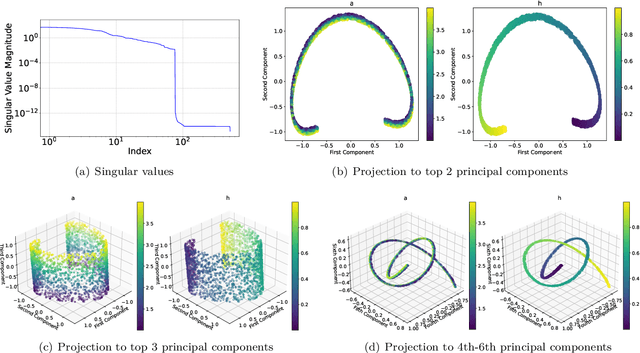
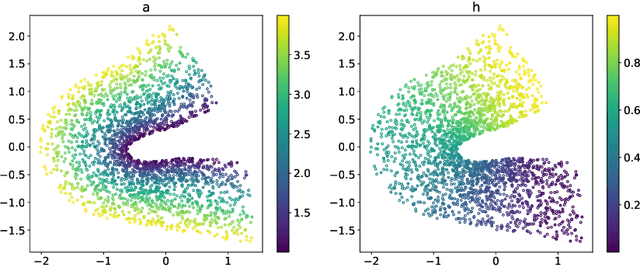
Many physical processes in science and engineering are naturally represented by operators between infinite-dimensional function spaces. The problem of operator learning, in this context, seeks to extract these physical processes from empirical data, which is challenging due to the infinite or high dimensionality of data. An integral component in addressing this challenge is model reduction, which reduces both the data dimensionality and problem size. In this paper, we utilize low-dimensional nonlinear structures in model reduction by investigating Auto-Encoder-based Neural Network (AENet). AENet first learns the latent variables of the input data and then learns the transformation from these latent variables to corresponding output data. Our numerical experiments validate the ability of AENet to accurately learn the solution operator of nonlinear partial differential equations. Furthermore, we establish a mathematical and statistical estimation theory that analyzes the generalization error of AENet. Our theoretical framework shows that the sample complexity of training AENet is intricately tied to the intrinsic dimension of the modeled process, while also demonstrating the remarkable resilience of AENet to noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge