Multiscale Hodge Scattering Networks for Data Analysis

We propose new scattering networks for signals measured on simplicial complexes, which we call \emph{Multiscale Hodge Scattering Networks} (MHSNs). Our construction is based on multiscale basis dictionaries on simplicial complexes, i.e., the $\kappa$-GHWT and $\kappa$-HGLET, which we recently developed for simplices of dimension $\kappa \in \N$ in a given simplicial complex by generalizing the node-based Generalized Haar-Walsh Transform (GHWT) and Hierarchical Graph Laplacian Eigen Transform (HGLET). The $\kappa$-GHWT and the $\kk$-HGLET both form redundant sets (i.e., dictionaries) of multiscale basis vectors and the corresponding expansion coefficients of a given signal. Our MHSNs use a layered structure analogous to a convolutional neural network (CNN) to cascade the moments of the modulus of the dictionary coefficients. The resulting features are invariant to reordering of the simplices (i.e., node permutation of the underlying graphs). Importantly, the use of multiscale basis dictionaries in our MHSNs admits a natural pooling operation that is akin to local pooling in CNNs, and which may be performed either locally or per-scale. These pooling operations are harder to define in both traditional scattering networks based on Morlet wavelets, and geometric scattering networks based on Diffusion Wavelets. As a result, we are able to extract a rich set of descriptive yet robust features that can be used along with very simple machine learning methods (i.e., logistic regression or support vector machines) to achieve high-accuracy classification systems with far fewer parameters to train than most modern graph neural networks. Finally, we demonstrate the usefulness of our MHSNs in three distinct types of problems: signal classification, domain (i.e., graph/simplex) classification, and molecular dynamics prediction.

Multiscale Transforms for Signals on Simplicial Complexes

Our previous multiscale graph basis dictionaries/graph signal transforms -- Generalized Haar-Walsh Transform (GHWT); Hierarchical Graph Laplacian Eigen Transform (HGLET); Natural Graph Wavelet Packets (NGWPs); and their relatives -- were developed for analyzing data recorded on nodes of a given graph. In this article, we propose their generalization for analyzing data recorded on edges, faces (i.e., triangles), or more generally $\kappa$-dimensional simplices of a simplicial complex (e.g., a triangle mesh of a manifold). The key idea is to use the Hodge Laplacians and their variants for hierarchical partitioning of a set of $\kappa$-dimensional simplices in a given simplicial complex, and then build localized basis functions on these partitioned subsets. We demonstrate their usefulness for data representation on both illustrative synthetic examples and real-world simplicial complexes generated from a co-authorship/citation dataset and an ocean current/flow dataset.

Semi-Supervised Manifold Learning with Complexity Decoupled Chart Autoencoders

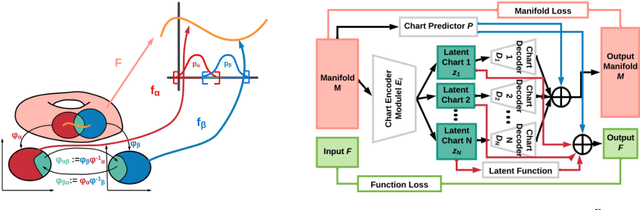
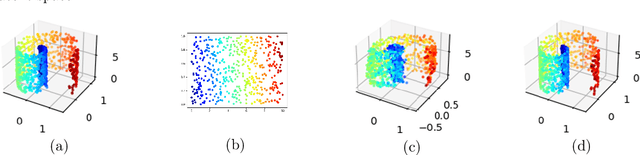
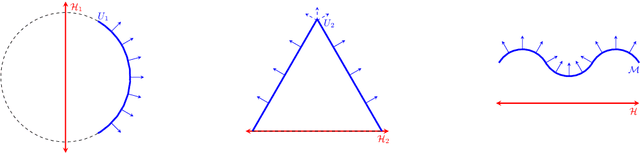
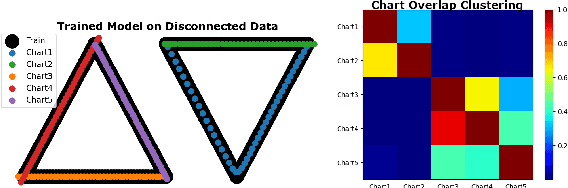
Autoencoding is a popular method in representation learning. Conventional autoencoders employ symmetric encoding-decoding procedures and a simple Euclidean latent space to detect hidden low-dimensional structures in an unsupervised way. This work introduces a chart autoencoder with an asymmetric encoding-decoding process that can incorporate additional semi-supervised information such as class labels. Besides enhancing the capability for handling data with complicated topological and geometric structures, these models can successfully differentiate nearby but disjoint manifolds and intersecting manifolds with only a small amount of supervision. Moreover, this model only requires a low complexity encoder, such as local linear projection. We discuss the theoretical approximation power of such networks that essentially depends on the intrinsic dimension of the data manifold and not the dimension of the observations. Our numerical experiments on synthetic and real-world data verify that the proposed model can effectively manage data with multi-class nearby but disjoint manifolds of different classes, overlapping manifolds, and manifolds with non-trivial topology.

Unsupervised Geometric Disentanglement for Surfaces via CFAN-VAE

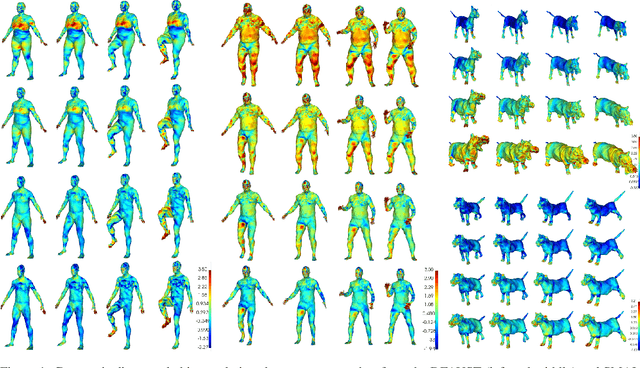
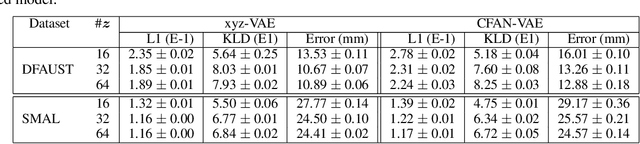
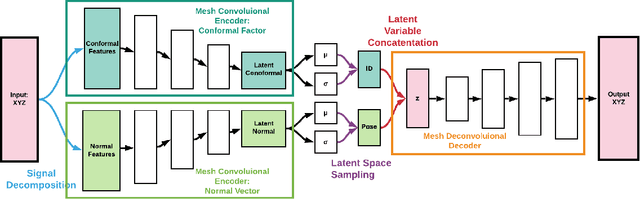
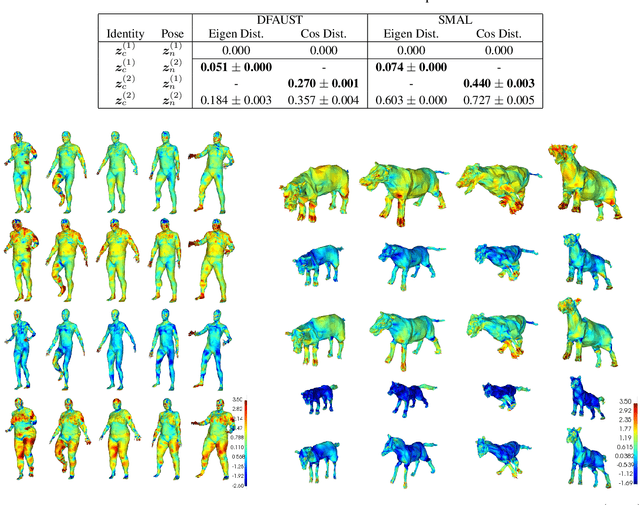
For non-Euclidean data such as meshes of humans, a prominent task for generative models is geometric disentanglement; the separation of latent codes for intrinsic (i.e. identity) and extrinsic (i.e. pose) geometry. This work introduces a novel mesh feature, the conformal factor and normal feature (CFAN), for use in mesh convolutional autoencoders. We further propose CFAN-VAE, a novel architecture that disentangles identity and pose using the CFAN feature and parallel transport convolution. CFAN-VAE achieves this geometric disentanglement in an unsupervised way, as it does not require label information on the identity or pose during training. Our comprehensive experiments, including reconstruction, interpolation, generation, and canonical correlation analysis, validate the effectiveness of the unsupervised geometric disentanglement. We also successfully detect and recover geometric disentanglement in mesh convolutional autoencoders that encode xyz-coordinates directly by registering its latent space to that of CFAN-VAE.

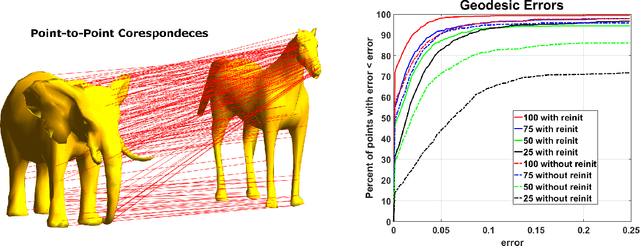
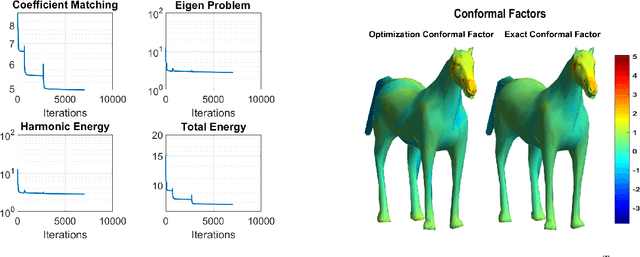
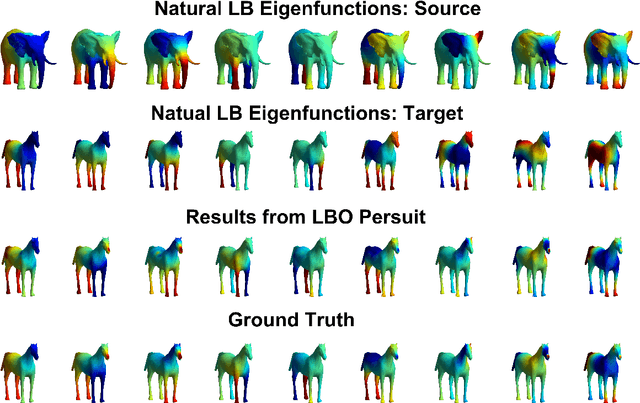
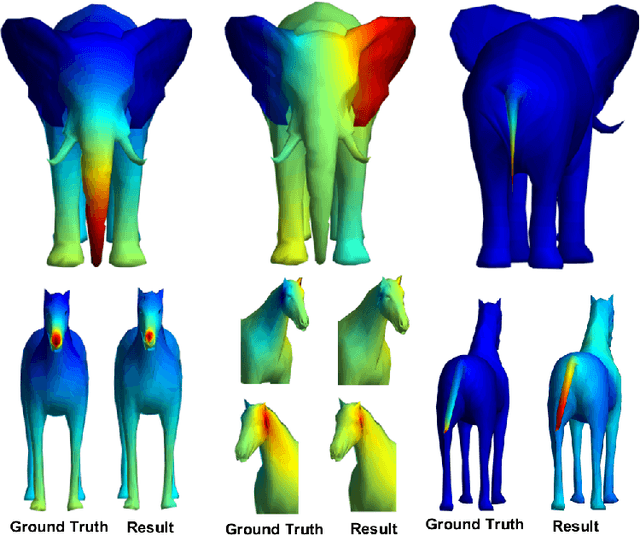
Nonisometric Surface Registration via Conformal Laplace-Beltrami Basis Pursuit

Surface registration is one of the most fundamental problems in geometry processing. Many approaches have been developed to tackle this problem in cases where the surfaces are nearly isometric. However, it is much more challenging to compute correspondence between surfaces which are intrinsically less similar. In this paper, we propose a variational model to align the Laplace-Beltrami (LB) eigensytems of two non-isometric genus zero shapes via conformal deformations. This method enables us compute to geometric meaningful point-to-point maps between non-isometric shapes. Our model is based on a novel basis pursuit scheme whereby we simultaneously compute a conformal deformation of a 'target shape' and its deformed LB eigensytem. We solve the model using an proximal alternating minimization algorithm hybridized with the augmented Lagrangian method which produces accurate correspondences given only a few landmark points. We also propose a reinitialization scheme to overcome some of the difficulties caused by the non-convexity of the variational problem. Intensive numerical experiments illustrate the effectiveness and robustness of the proposed method to handle non-isometric surfaces with large deformation with respect to both noise on the underlying manifolds and errors within the given landmarks.

Parallel Transport Convolution: A New Tool for Convolutional Neural Networks on Manifolds

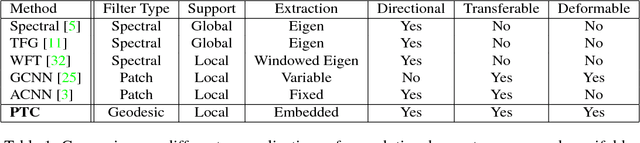
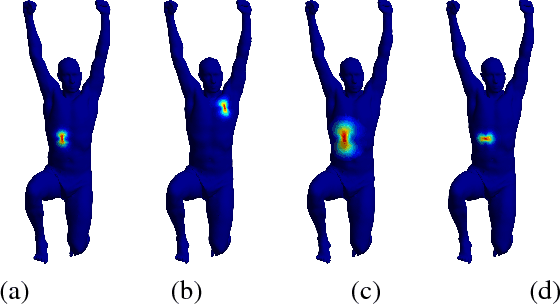
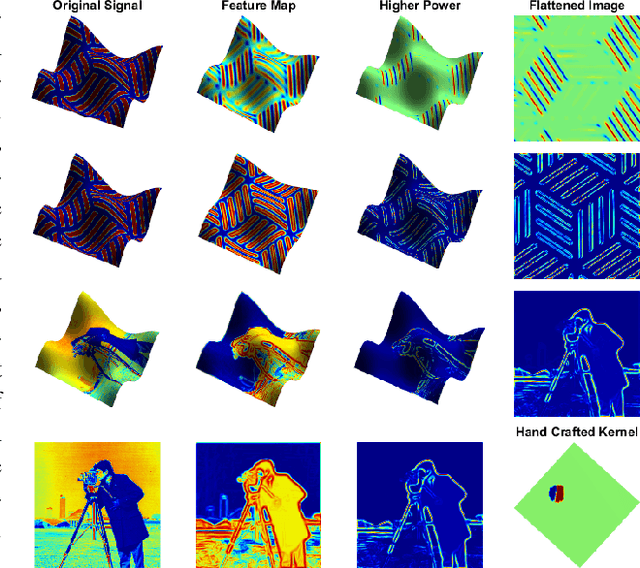
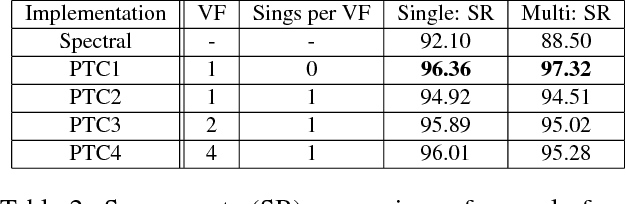
Convolution has been playing a prominent role in various applications in science and engineering for many years. It is the most important operation in convolutional neural networks. There has been a recent growth of interests of research in generalizing convolutions on curved domains such as manifolds and graphs. However, existing approaches cannot preserve all the desirable properties of Euclidean convolutions, namely compactly supported filters, directionality, transferability across different manifolds. In this paper we develop a new generalization of the convolution operation, referred to as parallel transport convolution (PTC), on Riemannian manifolds and their discrete counterparts. PTC is designed based on the parallel transportation which is able to translate information along a manifold and to intrinsically preserve directionality. PTC allows for the construction of compactly supported filters and is also robust to manifold deformations. This enables us to preform wavelet-like operations and to define deep convolutional neural networks on curved domains.