A Novel Multiscale Spatial Phase Estimate with the Structure Multivector

The monogenic signal (MS) was introduced by Felsberg and Sommer, and independently by Larkin under the name vortex operator. It is a two-dimensional (2D) analog of the well-known analytic signal, and allows for direct amplitude and phase demodulation of (amplitude and phase) modulated images so long as the signal is intrinsically one-dimensional (i1D). Felsberg's PhD dissertation also introduced the structure multivector (SMV), a model allowing for intrinsically 2D (i2D) structure. While the monogenic signal has become a well-known tool in the image processing community, the SMV is little used, although even in the case of i1D signals it provides a more robust orientation estimation than the MS. We argue the SMV is more suitable in standard i1D image feature extraction due to the this improvement, and extend the steerable wavelet frames of Held et al. to accommodate the additional features of the SMV. We then propose a novel quality map based on local orientation variance that yields a multiscale phase estimate which performs well even when SNR $\ge 1$. The performance is evaluated on several synthetic phase estimation tasks as well as on a fine-scale fingerprint registration task related to the 2D phase demodulation problem.

Multiscale Hodge Scattering Networks for Data Analysis

We propose new scattering networks for signals measured on simplicial complexes, which we call \emph{Multiscale Hodge Scattering Networks} (MHSNs). Our construction is based on multiscale basis dictionaries on simplicial complexes, i.e., the $\kappa$-GHWT and $\kappa$-HGLET, which we recently developed for simplices of dimension $\kappa \in \N$ in a given simplicial complex by generalizing the node-based Generalized Haar-Walsh Transform (GHWT) and Hierarchical Graph Laplacian Eigen Transform (HGLET). The $\kappa$-GHWT and the $\kk$-HGLET both form redundant sets (i.e., dictionaries) of multiscale basis vectors and the corresponding expansion coefficients of a given signal. Our MHSNs use a layered structure analogous to a convolutional neural network (CNN) to cascade the moments of the modulus of the dictionary coefficients. The resulting features are invariant to reordering of the simplices (i.e., node permutation of the underlying graphs). Importantly, the use of multiscale basis dictionaries in our MHSNs admits a natural pooling operation that is akin to local pooling in CNNs, and which may be performed either locally or per-scale. These pooling operations are harder to define in both traditional scattering networks based on Morlet wavelets, and geometric scattering networks based on Diffusion Wavelets. As a result, we are able to extract a rich set of descriptive yet robust features that can be used along with very simple machine learning methods (i.e., logistic regression or support vector machines) to achieve high-accuracy classification systems with far fewer parameters to train than most modern graph neural networks. Finally, we demonstrate the usefulness of our MHSNs in three distinct types of problems: signal classification, domain (i.e., graph/simplex) classification, and molecular dynamics prediction.

Multiscale Transforms for Signals on Simplicial Complexes

Our previous multiscale graph basis dictionaries/graph signal transforms -- Generalized Haar-Walsh Transform (GHWT); Hierarchical Graph Laplacian Eigen Transform (HGLET); Natural Graph Wavelet Packets (NGWPs); and their relatives -- were developed for analyzing data recorded on nodes of a given graph. In this article, we propose their generalization for analyzing data recorded on edges, faces (i.e., triangles), or more generally $\kappa$-dimensional simplices of a simplicial complex (e.g., a triangle mesh of a manifold). The key idea is to use the Hodge Laplacians and their variants for hierarchical partitioning of a set of $\kappa$-dimensional simplices in a given simplicial complex, and then build localized basis functions on these partitioned subsets. We demonstrate their usefulness for data representation on both illustrative synthetic examples and real-world simplicial complexes generated from a co-authorship/citation dataset and an ocean current/flow dataset.

The Scattering Transform Network with Generalized Morse Wavelets and Its Application to Music Genre Classification

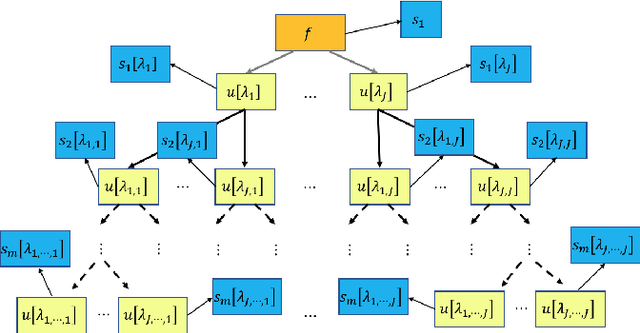
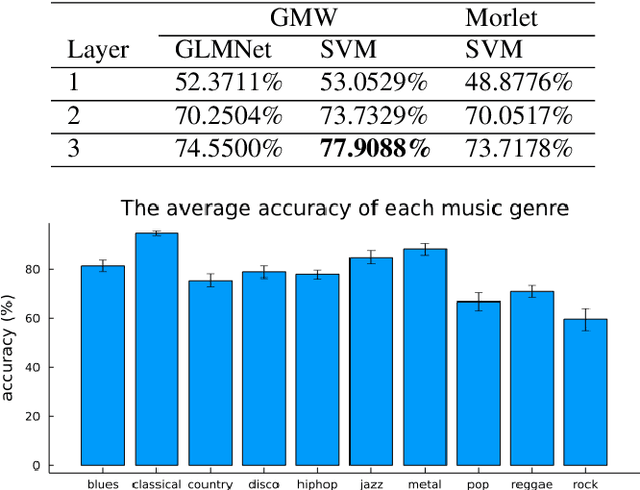
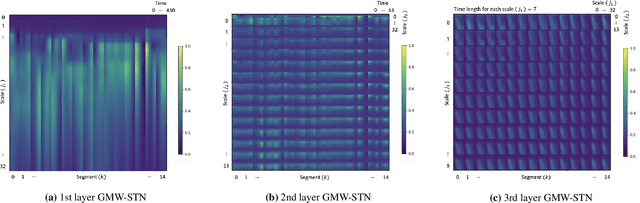
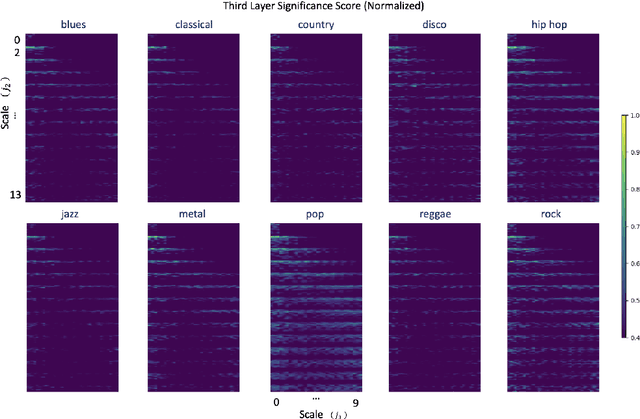
We propose to use the Generalized Morse Wavelets (GMWs) instead of commonly-used Morlet (or Gabor) wavelets in the Scattering Transform Network (STN), which we call the GMW-STN, for signal classification problems. The GMWs form a parameterized family of truly analytic wavelets while the Morlet wavelets are only approximately analytic. The analyticity of underlying wavelet filters in the STN is particularly important for nonstationary oscillatory signals such as music signals because it improves interpretability of the STN representations by providing multiscale amplitude and phase (and consequently frequency) information of input signals. We demonstrate the superiority of the GMW-STN over the conventional STN in music genre classification using the so-called GTZAN database. Moreover, we show the performance improvement of the GMW-STN by increasing its number of layers to three over the typical two-layer STN.}

Monogenic Wavelet Scattering Network for Texture Image Classification

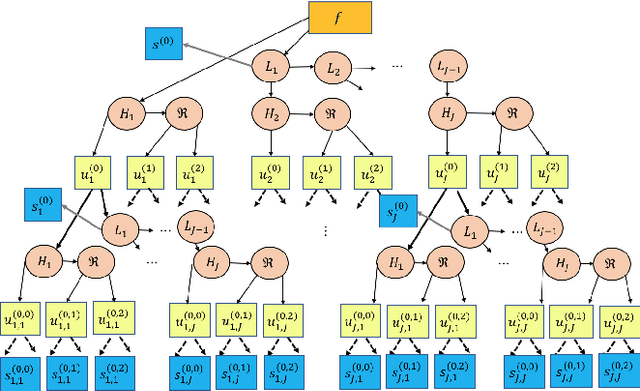
The scattering transform network (STN), which has a similar structure as that of a popular convolutional neural network except its use of predefined convolution filters and a small number of layers, can generates a robust representation of an input signal relative to small deformations. We propose a novel Monogenic Wavelet Scattering Network (MWSN) for 2D texture image classification through a cascade of monogenic wavelet filtering with nonlinear modulus and averaging operators by replacing the 2D Morlet wavelet filtering in the standard STN. Our MWSN can extract useful hierarchical and directional features with interpretable coefficients, which can be further compressed by PCA and fed into a classifier. Using the CUReT texture image database, we demonstrate the superior performance of our MWSN over the standard STN. This performance improvement can be explained by the natural extension of 1D analyticity to 2D monogenicity.

eGHWT: The extended Generalized Haar-Walsh Transform

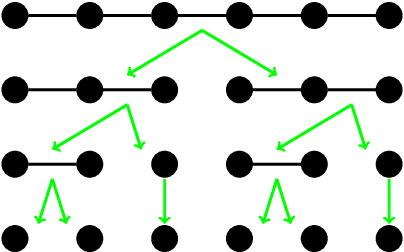
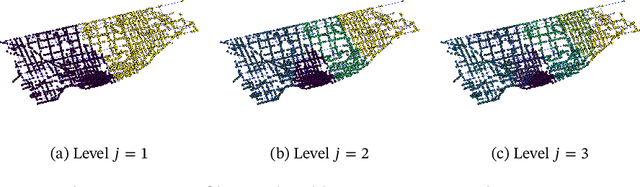
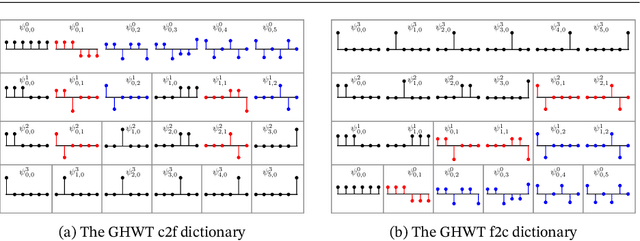
Extending computational harmonic analysis tools from the classical setting of regular lattices to the more general setting of graphs and networks is very important and much research has been done recently. The Generalized Haar-Walsh Transform (GHWT) developed by Irion and Saito (2014) is a multiscale transform for signals on graphs, which is a generalization of the classical Haar and Walsh-Hadamard Transforms. We propose the extended Generalized Haar-Walsh Transform (eGHWT), which is a generalization of the adapted time-frequency tilings of Thiele and Villemoes (1996). The eGHWT examines not only the efficiency of graph-domain partitions but also that of "sequency-domain" partitions simultaneously. Consequently, the eGHWT and its associated best-basis selection algorithm for graph signals significantly improve the performance of the previous GHWT with the similar computational cost, $O(N \log N)$, where $N$ is the number of nodes of an input graph. While the GHWT best-basis algorithm seeks the most suitable orthonormal basis for a given task among more than $(1.5)^N$ possible orthonormal bases in $\mathbb{R}^N$, the eGHWT best-basis algorithm can find a better one by searching through more than $0.618\cdot(1.84)^N$ possible orthonormal bases in $\mathbb{R}^N$. This article describes the details of the eGHWT best-basis algorithm and demonstrates its superiority using several examples including genuine graph signals as well as conventional digital images viewed as graph signals. Furthermore, we also show how the eGHWT can be extended to 2D signals and matrix-form data by viewing them as a tensor product of graphs generated from their columns and rows and demonstrate its effectiveness on applications such as image approximation.

The Use of Mutual Coherence to Prove $\ell^1/\ell^0$-Equivalence in Classification Problems

We consider the decomposition of a signal over an overcomplete set of vectors. Minimization of the $\ell^1$-norm of the coefficient vector can often retrieve the sparsest solution (so-called "$\ell^1/\ell^0$-equivalence"), a generally NP-hard task, and this fact has powered the field of compressed sensing. Wright et al.'s sparse representation-based classification (SRC) applies this relationship to machine learning, wherein the signal to be decomposed represents the test sample and columns of the dictionary are training samples. We investigate the relationships between $\ell^1$-minimization, sparsity, and classification accuracy in SRC. After proving that the tractable, deterministic approach to verifying $\ell^1/\ell^0$-equivalence fundamentally conflicts with the high coherence between same-class training samples, we demonstrate that $\ell^1$-minimization can still recover the sparsest solution when the classes are well-separated. Further, using a nonlinear transform so that sparse recovery conditions may be satisfied, we demonstrate that approximate (not strict) equivalence is key to the success of SRC.

Improving Sparse Representation-Based Classification Using Local Principal Component Analysis

Sparse representation-based classification (SRC), proposed by Wright et al., seeks the sparsest decomposition of a test sample over the dictionary of training samples, with classification to the most-contributing class. Because it assumes test samples can be written as linear combinations of their same-class training samples, the success of SRC depends on the size and representativeness of the training set. Our proposed classification algorithm enlarges the training set by using local principal component analysis to approximate the basis vectors of the tangent hyperplane of the class manifold at each training sample. The dictionary in SRC is replaced by a local dictionary that adapts to the test sample and includes training samples and their corresponding tangent basis vectors. We use a synthetic data set and three face databases to demonstrate that this method can achieve higher classification accuracy than SRC in cases of sparse sampling, nonlinear class manifolds, and stringent dimension reduction.

Underwater object classification using scattering transform of sonar signals

In this paper, we apply the scattering transform (ST), a nonlinear map based off of a convolutional neural network (CNN), to classification of underwater objects using sonar signals. The ST formalizes the observation that the filters learned by a CNN have wavelet like structure. We achieve effective binary classification both on a real dataset of Unexploded Ordinance (UXOs), as well as synthetically generated examples. We also explore the effects on the waveforms with respect to changes in the object domain (e.g., translation, rotation, and acoustic impedance, etc.), and examine the consequences coming from theoretical results for the scattering transform. We show that the scattering transform is capable of excellent classification on both the synthetic and real problems, thanks to having more quasi-invariance properties that are well-suited to translation and rotation of the object.