The Scattering Transform Network with Generalized Morse Wavelets and Its Application to Music Genre Classification

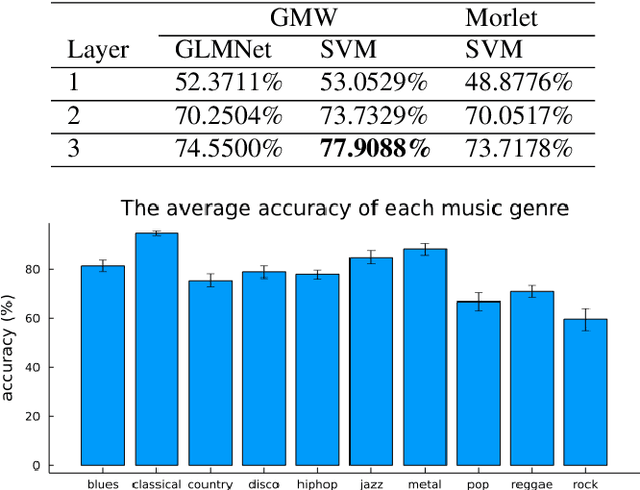
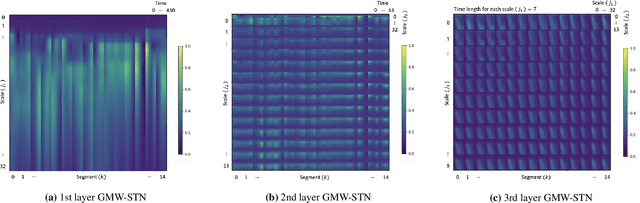
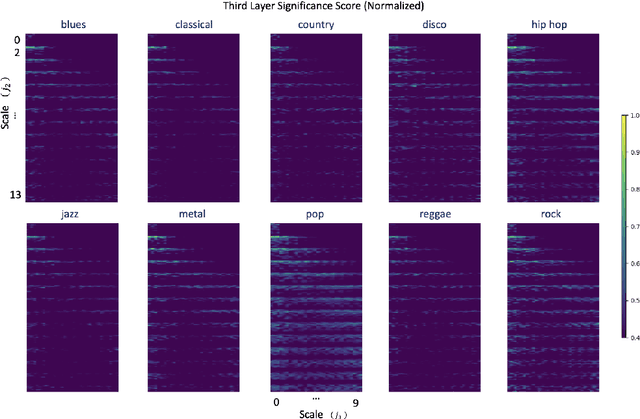
We propose to use the Generalized Morse Wavelets (GMWs) instead of commonly-used Morlet (or Gabor) wavelets in the Scattering Transform Network (STN), which we call the GMW-STN, for signal classification problems. The GMWs form a parameterized family of truly analytic wavelets while the Morlet wavelets are only approximately analytic. The analyticity of underlying wavelet filters in the STN is particularly important for nonstationary oscillatory signals such as music signals because it improves interpretability of the STN representations by providing multiscale amplitude and phase (and consequently frequency) information of input signals. We demonstrate the superiority of the GMW-STN over the conventional STN in music genre classification using the so-called GTZAN database. Moreover, we show the performance improvement of the GMW-STN by increasing its number of layers to three over the typical two-layer STN.}

Monogenic Wavelet Scattering Network for Texture Image Classification

The scattering transform network (STN), which has a similar structure as that of a popular convolutional neural network except its use of predefined convolution filters and a small number of layers, can generates a robust representation of an input signal relative to small deformations. We propose a novel Monogenic Wavelet Scattering Network (MWSN) for 2D texture image classification through a cascade of monogenic wavelet filtering with nonlinear modulus and averaging operators by replacing the 2D Morlet wavelet filtering in the standard STN. Our MWSN can extract useful hierarchical and directional features with interpretable coefficients, which can be further compressed by PCA and fed into a classifier. Using the CUReT texture image database, we demonstrate the superior performance of our MWSN over the standard STN. This performance improvement can be explained by the natural extension of 1D analyticity to 2D monogenicity.

Subsampled Turbulence Removal Network

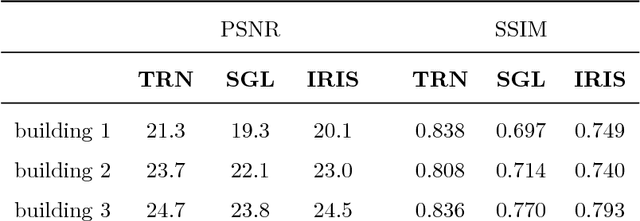
We present a deep-learning approach to restore a sequence of turbulence-distorted video frames from turbulent deformations and space-time varying blurs. Instead of requiring a massive training sample size in deep networks, we purpose a training strategy that is based on a new data augmentation method to model turbulence from a relatively small dataset. Then we introduce a subsampled method to enhance the restoration performance of the presented GAN model. The contributions of the paper is threefold: first, we introduce a simple but effective data augmentation algorithm to model the turbulence in real life for training in the deep network; Second, we firstly purpose the Wasserstein GAN combined with $\ell_1$ cost for successful restoration of turbulence-corrupted video sequence; Third, we combine the subsampling algorithm to filter out strongly corrupted frames to generate a video sequence with better quality.