Alex Havrilla
Synthetic Problem Generation for Reasoning via Quality-Diversity Algorithms
Jun 06, 2025Abstract:Large language model (LLM) driven synthetic data generation has emerged as a powerful method for improving model reasoning capabilities. However, most methods either distill large state-of-the-art models into small students or use natural ground-truth problem statements to guarantee problem statement quality. This limits the scalability of these approaches to more complex and diverse problem domains. To address this, we present SPARQ: Synthetic Problem Generation for Reasoning via Quality-Diversity Algorithms, a novel approach for generating high-quality and diverse synthetic math problem and solution pairs using only a single model by measuring a problem's solve-rate: a proxy for problem difficulty. Starting from a seed dataset of 7.5K samples, we generate over 20 million new problem-solution pairs. We show that filtering the generated data by difficulty and then fine-tuning the same model on the resulting data improves relative model performance by up to 24\%. Additionally, we conduct ablations studying the impact of synthetic data quantity, quality and diversity on model generalization. We find that higher quality, as measured by problem difficulty, facilitates better in-distribution performance. Further, while generating diverse synthetic data does not as strongly benefit in-distribution performance, filtering for more diverse data facilitates more robust OOD generalization. We also confirm the existence of model and data scaling laws for synthetically generated problems, which positively benefit downstream model generalization.
Transformers for Learning on Noisy and Task-Level Manifolds: Approximation and Generalization Insights
May 06, 2025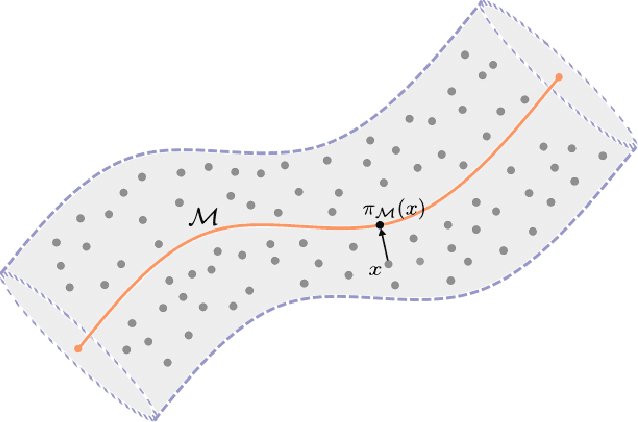
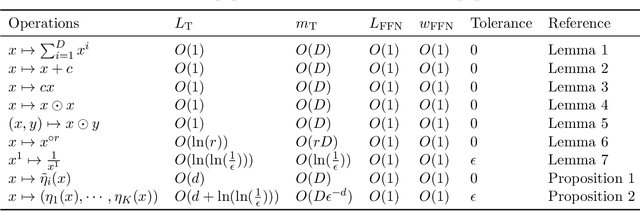


Abstract:Transformers serve as the foundational architecture for large language and video generation models, such as GPT, BERT, SORA and their successors. Empirical studies have demonstrated that real-world data and learning tasks exhibit low-dimensional structures, along with some noise or measurement error. The performance of transformers tends to depend on the intrinsic dimension of the data/tasks, though theoretical understandings remain largely unexplored for transformers. This work establishes a theoretical foundation by analyzing the performance of transformers for regression tasks involving noisy input data on a manifold. Specifically, the input data are in a tubular neighborhood of a manifold, while the ground truth function depends on the projection of the noisy data onto the manifold. We prove approximation and generalization errors which crucially depend on the intrinsic dimension of the manifold. Our results demonstrate that transformers can leverage low-complexity structures in learning task even when the input data are perturbed by high-dimensional noise. Our novel proof technique constructs representations of basic arithmetic operations by transformers, which may hold independent interest.
IGDA: Interactive Graph Discovery through Large Language Model Agents
Feb 24, 2025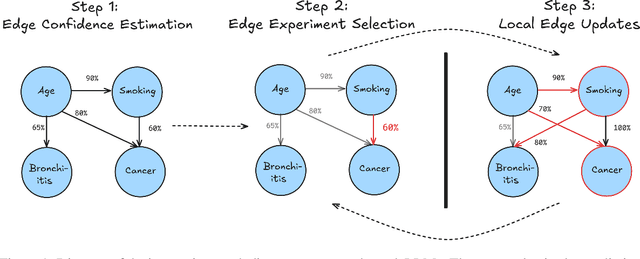
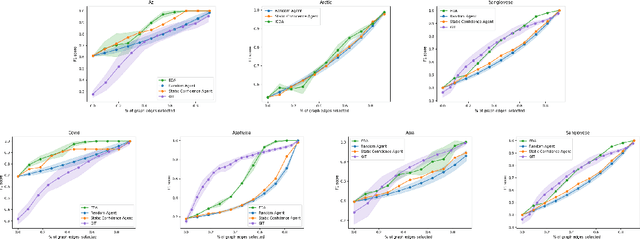
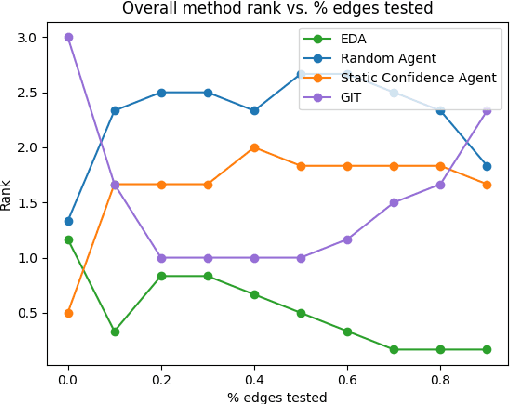
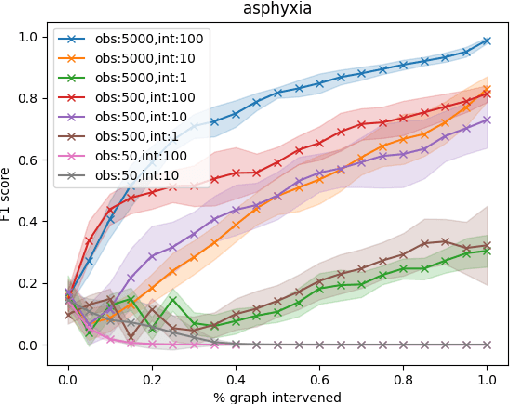
Abstract:Large language models ($\textbf{LLMs}$) have emerged as a powerful method for discovery. Instead of utilizing numerical data, LLMs utilize associated variable $\textit{semantic metadata}$ to predict variable relationships. Simultaneously, LLMs demonstrate impressive abilities to act as black-box optimizers when given an objective $f$ and sequence of trials. We study LLMs at the intersection of these two capabilities by applying LLMs to the task of $\textit{interactive graph discovery}$: given a ground truth graph $G^*$ capturing variable relationships and a budget of $I$ edge experiments over $R$ rounds, minimize the distance between the predicted graph $\hat{G}_R$ and $G^*$ at the end of the $R$-th round. To solve this task we propose $\textbf{IGDA}$, a LLM-based pipeline incorporating two key components: 1) an LLM uncertainty-driven method for edge experiment selection 2) a local graph update strategy utilizing binary feedback from experiments to improve predictions for unselected neighboring edges. Experiments on eight different real-world graphs show our approach often outperforms all baselines including a state-of-the-art numerical method for interactive graph discovery. Further, we conduct a rigorous series of ablations dissecting the impact of each pipeline component. Finally, to assess the impact of memorization, we apply our interactive graph discovery strategy to a complex, new (as of July 2024) causal graph on protein transcription factors, finding strong performance in a setting where memorization is impossible. Overall, our results show IGDA to be a powerful method for graph discovery complementary to existing numerically driven approaches.
Surveying the Effects of Quality, Diversity, and Complexity in Synthetic Data From Large Language Models
Dec 04, 2024



Abstract:Synthetic data generation with Large Language Models is a promising paradigm for augmenting natural data over a nearly infinite range of tasks. Given this variety, direct comparisons among synthetic data generation algorithms are scarce, making it difficult to understand where improvement comes from and what bottlenecks exist. We propose to evaluate algorithms via the makeup of synthetic data generated by each algorithm in terms of data quality, diversity, and complexity. We choose these three characteristics for their significance in open-ended processes and the impact each has on the capabilities of downstream models. We find quality to be essential for in-distribution model generalization, diversity to be essential for out-of-distribution generalization, and complexity to be beneficial for both. Further, we emphasize the existence of Quality-Diversity trade-offs in training data and the downstream effects on model performance. We then examine the effect of various components in the synthetic data pipeline on each data characteristic. This examination allows us to taxonomize and compare synthetic data generation algorithms through the components they utilize and the resulting effects on data QDC composition. This analysis extends into a discussion on the importance of balancing QDC in synthetic data for efficient reinforcement learning and self-improvement algorithms. Analogous to the QD trade-offs in training data, often there exist trade-offs between model output quality and output diversity which impact the composition of synthetic data. We observe that many models are currently evaluated and optimized only for output quality, thereby limiting output diversity and the potential for self-improvement. We argue that balancing these trade-offs is essential to the development of future self-improvement algorithms and highlight a number of works making progress in this direction.
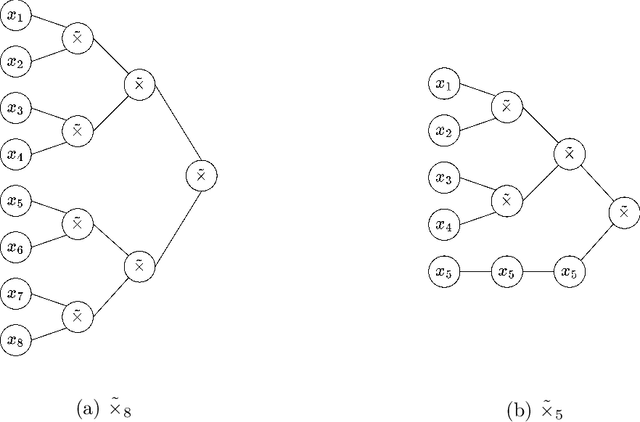
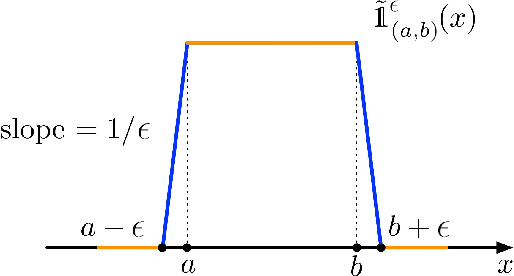
Understanding Scaling Laws with Statistical and Approximation Theory for Transformer Neural Networks on Intrinsically Low-dimensional Data
Nov 11, 2024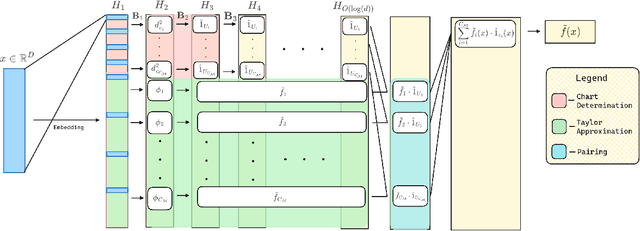
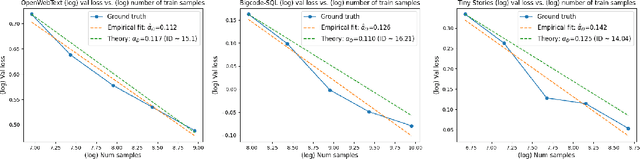
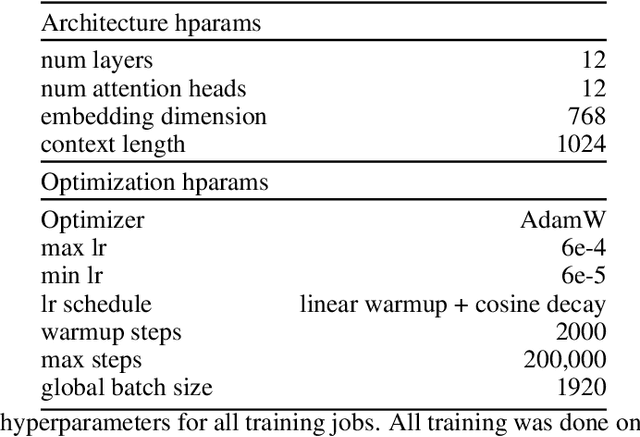
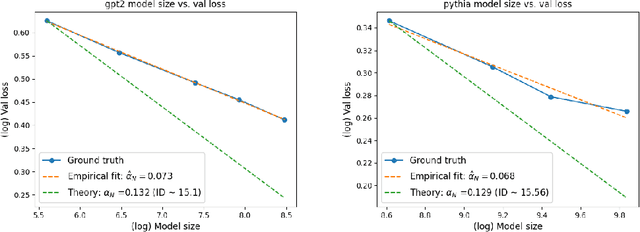
Abstract:When training deep neural networks, a model's generalization error is often observed to follow a power scaling law dependent both on the model size and the data size. Perhaps the best known example of such scaling laws are for transformer-based large language models, where networks with billions of parameters are trained on trillions of tokens of text. Yet, despite sustained widespread interest, a rigorous understanding of why transformer scaling laws exist is still missing. To answer this question, we establish novel statistical estimation and mathematical approximation theories for transformers when the input data are concentrated on a low-dimensional manifold. Our theory predicts a power law between the generalization error and both the training data size and the network size for transformers, where the power depends on the intrinsic dimension $d$ of the training data. Notably, the constructed model architecture is shallow, requiring only logarithmic depth in $d$. By leveraging low-dimensional data structures under a manifold hypothesis, we are able to explain transformer scaling laws in a way which respects the data geometry. Moreover, we test our theory with empirical observation by training LLMs on natural language datasets. We find the observed empirical data scaling laws closely agree with our theoretical predictions. Taken together, these results rigorously show the intrinsic dimension of data to be a crucial quantity affecting transformer scaling laws in both theory and practice.
Teaching Large Language Models to Reason with Reinforcement Learning
Mar 07, 2024



Abstract:Reinforcement Learning from Human Feedback (\textbf{RLHF}) has emerged as a dominant approach for aligning LLM outputs with human preferences. Inspired by the success of RLHF, we study the performance of multiple algorithms that learn from feedback (Expert Iteration, Proximal Policy Optimization (\textbf{PPO}), Return-Conditioned RL) on improving LLM reasoning capabilities. We investigate both sparse and dense rewards provided to the LLM both heuristically and via a learned reward model. We additionally start from multiple model sizes and initializations both with and without supervised fine-tuning (\textbf{SFT}) data. Overall, we find all algorithms perform comparably, with Expert Iteration performing best in most cases. Surprisingly, we find the sample complexity of Expert Iteration is similar to that of PPO, requiring at most on the order of $10^6$ samples to converge from a pretrained checkpoint. We investigate why this is the case, concluding that during RL training models fail to explore significantly beyond solutions already produced by SFT models. Additionally, we discuss a trade off between maj@1 and pass@96 metric performance during SFT training and how conversely RL training improves both simultaneously. We then conclude by discussing the implications of our findings for RLHF and the future role of RL in LLM fine-tuning.
GLoRe: When, Where, and How to Improve LLM Reasoning via Global and Local Refinements
Feb 13, 2024



Abstract:State-of-the-art language models can exhibit impressive reasoning refinement capabilities on math, science or coding tasks. However, recent work demonstrates that even the best models struggle to identify \textit{when and where to refine} without access to external feedback. Outcome-based Reward Models (\textbf{ORMs}), trained to predict correctness of the final answer indicating when to refine, offer one convenient solution for deciding when to refine. Process Based Reward Models (\textbf{PRMs}), trained to predict correctness of intermediate steps, can then be used to indicate where to refine. But they are expensive to train, requiring extensive human annotations. In this paper, we propose Stepwise ORMs (\textbf{SORMs}) which are trained, only on synthetic data, to approximate the expected future reward of the optimal policy or $V^{\star}$. More specifically, SORMs are trained to predict the correctness of the final answer when sampling the current policy many times (rather than only once as in the case of ORMs). Our experiments show that SORMs can more accurately detect incorrect reasoning steps compared to ORMs, thus improving downstream accuracy when doing refinements. We then train \textit{global} refinement models, which take only the question and a draft solution as input and predict a corrected solution, and \textit{local} refinement models which also take as input a critique indicating the location of the first reasoning error. We generate training data for both models synthetically by reusing data used to train the SORM. We find combining global and local refinements, using the ORM as a reranker, significantly outperforms either one individually, as well as a best of three sample baseline. With this strategy we can improve the accuracy of a LLaMA-2 13B model (already fine-tuned with RL) on GSM8K from 53\% to 65\% when greedily sampled.
Understanding the Effect of Noise in LLM Training Data with Algorithmic Chains of Thought
Feb 09, 2024Abstract:During both pretraining and fine-tuning, Large Language Models (\textbf{LLMs}) are trained on trillions of tokens of text of widely varying quality. Both phases of training typically involve heuristically filtering out ``low-quality'' or \textit{noisy} training samples, yet little is known quantitatively about how the type or intensity of noise affects downstream performance. In this work, we study how noise in chain of thought (\textbf{CoT}) impacts task performance in the highly-controlled setting of algorithmically solvable tasks. First, we develop the Traced Integer (\textbf{TInt}) framework to generate highly customizable noised execution traces for any arithmetic function on lists of integers. We then define two types of noise: \textit{static} noise, a local form of noise which is applied after the CoT trace is computed, and \textit{dynamic} noise, a global form of noise which propagates errors in the trace as it is computed. We then evaluate the test performance of pretrained models both prompted and fine-tuned on noised datasets with varying levels of dataset contamination and intensity. We find fine-tuned models are extremely robust to high levels of static noise but struggle significantly more with lower levels of dynamic noise. In contrast, few-shot prompted models appear more sensitive to even static noise. We conclude with a discussion of how our findings impact noise filtering best-practices, in particular emphasizing the importance of removing samples containing destructive dynamic noise with global errors.
Deep Nonparametric Estimation of Intrinsic Data Structures by Chart Autoencoders: Generalization Error and Robustness
Mar 20, 2023

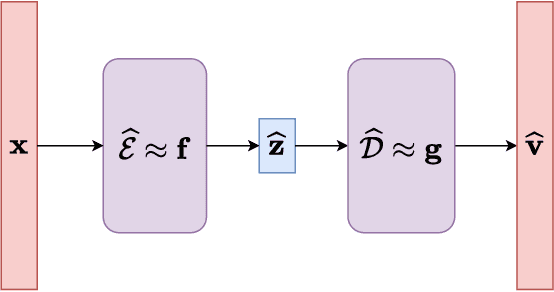
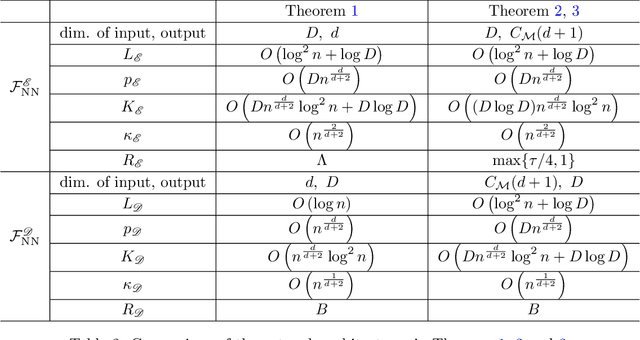
Abstract:Autoencoders have demonstrated remarkable success in learning low-dimensional latent features of high-dimensional data across various applications. Assuming that data are sampled near a low-dimensional manifold, we employ chart autoencoders, which encode data into low-dimensional latent features on a collection of charts, preserving the topology and geometry of the data manifold. Our paper establishes statistical guarantees on the generalization error of chart autoencoders, and we demonstrate their denoising capabilities by considering $n$ noisy training samples, along with their noise-free counterparts, on a $d$-dimensional manifold. By training autoencoders, we show that chart autoencoders can effectively denoise the input data with normal noise. We prove that, under proper network architectures, chart autoencoders achieve a squared generalization error in the order of $\displaystyle n^{-\frac{2}{d+2}}\log^4 n$, which depends on the intrinsic dimension of the manifold and only weakly depends on the ambient dimension and noise level. We further extend our theory on data with noise containing both normal and tangential components, where chart autoencoders still exhibit a denoising effect for the normal component. As a special case, our theory also applies to classical autoencoders, as long as the data manifold has a global parametrization. Our results provide a solid theoretical foundation for the effectiveness of autoencoders, which is further validated through several numerical experiments.
On Deep Generative Models for Approximation and Estimation of Distributions on Manifolds
Feb 25, 2023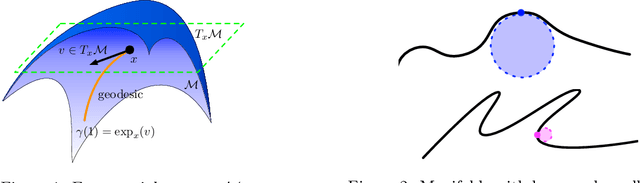
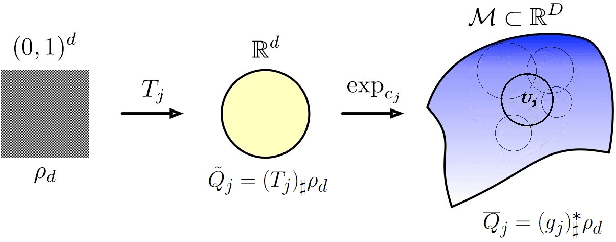
Abstract:Generative networks have experienced great empirical successes in distribution learning. Many existing experiments have demonstrated that generative networks can generate high-dimensional complex data from a low-dimensional easy-to-sample distribution. However, this phenomenon can not be justified by existing theories. The widely held manifold hypothesis speculates that real-world data sets, such as natural images and signals, exhibit low-dimensional geometric structures. In this paper, we take such low-dimensional data structures into consideration by assuming that data distributions are supported on a low-dimensional manifold. We prove statistical guarantees of generative networks under the Wasserstein-1 loss. We show that the Wasserstein-1 loss converges to zero at a fast rate depending on the intrinsic dimension instead of the ambient data dimension. Our theory leverages the low-dimensional geometric structures in data sets and justifies the practical power of generative networks. We require no smoothness assumptions on the data distribution which is desirable in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge