Zhaiming Shen
Understanding In-Context Learning on Structured Manifolds: Bridging Attention to Kernel Methods
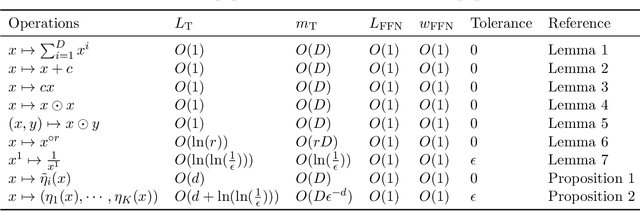
Jun 12, 2025Abstract:While in-context learning (ICL) has achieved remarkable success in natural language and vision domains, its theoretical understanding--particularly in the context of structured geometric data--remains unexplored. In this work, we initiate a theoretical study of ICL for regression of H\"older functions on manifolds. By establishing a novel connection between the attention mechanism and classical kernel methods, we derive generalization error bounds in terms of the prompt length and the number of training tasks. When a sufficient number of training tasks are observed, transformers give rise to the minimax regression rate of H\"older functions on manifolds, which scales exponentially with the intrinsic dimension of the manifold, rather than the ambient space dimension. Our result also characterizes how the generalization error scales with the number of training tasks, shedding light on the complexity of transformers as in-context algorithm learners. Our findings provide foundational insights into the role of geometry in ICL and novels tools to study ICL of nonlinear models.
Transformers for Learning on Noisy and Task-Level Manifolds: Approximation and Generalization Insights
May 06, 2025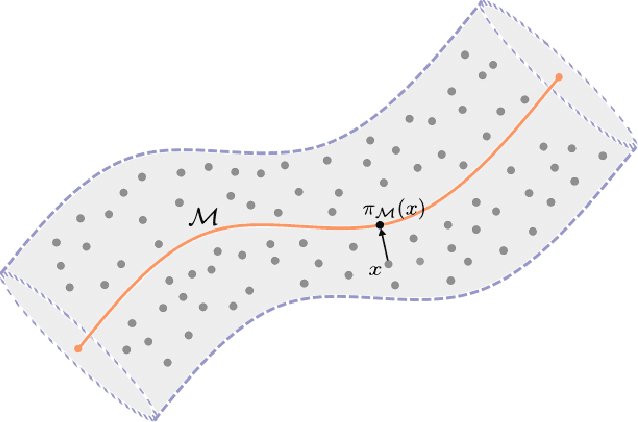


Abstract:Transformers serve as the foundational architecture for large language and video generation models, such as GPT, BERT, SORA and their successors. Empirical studies have demonstrated that real-world data and learning tasks exhibit low-dimensional structures, along with some noise or measurement error. The performance of transformers tends to depend on the intrinsic dimension of the data/tasks, though theoretical understandings remain largely unexplored for transformers. This work establishes a theoretical foundation by analyzing the performance of transformers for regression tasks involving noisy input data on a manifold. Specifically, the input data are in a tubular neighborhood of a manifold, while the ground truth function depends on the projection of the noisy data onto the manifold. We prove approximation and generalization errors which crucially depend on the intrinsic dimension of the manifold. Our results demonstrate that transformers can leverage low-complexity structures in learning task even when the input data are perturbed by high-dimensional noise. Our novel proof technique constructs representations of basic arithmetic operations by transformers, which may hold independent interest.
Graph-based Semi-supervised and Unsupervised Methods for Local Clustering
Apr 28, 2025Abstract:Local clustering aims to identify specific substructures within a large graph without requiring full knowledge of the entire graph. These substructures are typically small compared to the overall graph, enabling the problem to be approached by finding a sparse solution to a linear system associated with the graph Laplacian. In this work, we first propose a method for identifying specific local clusters when very few labeled data is given, which we term semi-supervised local clustering. We then extend this approach to the unsupervised setting when no prior information on labels is available. The proposed methods involve randomly sampling the graph, applying diffusion through local cluster extraction, then examining the overlap among the results to find each cluster. We establish the co-membership conditions for any pair of nodes and rigorously prove the correctness of our methods. Additionally, we conduct extensive experiments to demonstrate that the proposed methods achieve state-of-the-arts results in the low-label rates regime.
Local Clustering for Lung Cancer Image Classification via Sparse Solution Technique
Jul 11, 2024Abstract:In this work, we propose to use a local clustering approach based on the sparse solution technique to study the medical image, especially the lung cancer image classification task. We view images as the vertices in a weighted graph and the similarity between a pair of images as the edges in the graph. The vertices within the same cluster can be assumed to share similar features and properties, thus making the applications of graph clustering techniques very useful for image classification. Recently, the approach based on the sparse solutions of linear systems for graph clustering has been found to identify clusters more efficiently than traditional clustering methods such as spectral clustering. We propose to use the two newly developed local clustering methods based on sparse solution of linear system for image classification. In addition, we employ a box spline-based tight-wavelet-framelet method to clean these images and help build a better adjacency matrix before clustering. The performance of our methods is shown to be very effective in classifying images. Our approach is significantly more efficient and either favorable or equally effective compared with other state-of-the-art approaches. Finally, we shall make a remark by pointing out two image deformation methods to build up more artificial image data to increase the number of labeled images.
Tree-based Ensemble Learning for Out-of-distribution Detection
May 05, 2024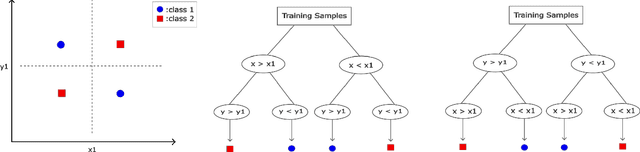


Abstract:Being able to successfully determine whether the testing samples has similar distribution as the training samples is a fundamental question to address before we can safely deploy most of the machine learning models into practice. In this paper, we propose TOOD detection, a simple yet effective tree-based out-of-distribution (TOOD) detection mechanism to determine if a set of unseen samples will have similar distribution as of the training samples. The TOOD detection mechanism is based on computing pairwise hamming distance of testing samples' tree embeddings, which are obtained by fitting a tree-based ensemble model through in-distribution training samples. Our approach is interpretable and robust for its tree-based nature. Furthermore, our approach is efficient, flexible to various machine learning tasks, and can be easily generalized to unsupervised setting. Extensive experiments are conducted to show the proposed method outperforms other state-of-the-art out-of-distribution detection methods in distinguishing the in-distribution from out-of-distribution on various tabular, image, and text data.
Maximal Volume Matrix Cross Approximation for Image Compression and Least Squares Solution
Sep 29, 2023



Abstract:We study the classic cross approximation of matrices based on the maximal volume submatrices. Our main results consist of an improvement of a classic estimate for matrix cross approximation and a greedy approach for finding the maximal volume submatrices. Indeed, we present a new proof of a classic estimate of the inequality with an improved constant. Also, we present a family of greedy maximal volume algorithms which improve the error bound of cross approximation of a matrix in the Chebyshev norm and also improve the computational efficiency of classic maximal volume algorithm. The proposed algorithms are shown to have theoretical guarantees of convergence. Finally, we present two applications: one is image compression and the other is least squares approximation of continuous functions. Our numerical results in the end of the paper demonstrate the effective performances of our approach.
Semi-supervised Local Cluster Extraction by Compressive Sensing
Nov 20, 2022Abstract:Local clustering problem aims at extracting a small local structure inside a graph without the necessity of knowing the entire graph structure. As the local structure is usually small in size compared to the entire graph, one can think of it as a compressive sensing problem where the indices of target cluster can be thought as a sparse solution to a linear system. In this paper, we propose a new semi-supervised local cluster extraction approach by applying the idea of compressive sensing based on two pioneering works under the same framework. Our approves improves the existing works by making the initial cut to be the entire graph and hence overcomes a major limitation of existing works, which is the low quality of initial cut. Extensive experimental results on multiple benchmark datasets demonstrate the effectiveness of our approach.
A Least Square Approach to Semi-supervised Local Cluster Extraction
Feb 07, 2022Abstract:A least square semi-supervised local clustering algorithm based on the idea of compressed sensing are proposed to extract clusters from a graph with known adjacency matrix. The algorithm is based on a two stage approaches similar to the one in \cite{LaiMckenzie2020}. However, under a weaker assumption and with less computational complexity than the one in \cite{LaiMckenzie2020}, the algorithm is shown to be able to find a desired cluster with high probability. Several numerical experiments including the synthetic data and real data such as MNIST, AT\&T and YaleB human faces data sets are conducted to demonstrate the performance of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge