A Formalization of Image Vectorization by Region Merging

Image vectorization converts raster images into vector graphics composed of regions separated by curves. Typical vectorization methods first define the regions by grouping similar colored regions via color quantization, then approximate their boundaries by Bezier curves. In that way, the raster input is converted into an SVG format parameterizing the regions' colors and the Bezier control points. This compact representation has many graphical applications thanks to its universality and resolution-independence. In this paper, we remark that image vectorization is nothing but an image segmentation, and that it can be built by fine to coarse region merging. Our analysis of the problem leads us to propose a vectorization method alternating region merging and curve smoothing. We formalize the method by alternate operations on the dual and primal graph induced from any domain partition. In that way, we address a limitation of current vectorization methods, which separate the update of regional information from curve approximation. We formalize region merging methods by associating them with various gain functionals, including the classic Beaulieu-Goldberg and Mumford-Shah functionals. More generally, we introduce and compare region merging criteria involving region number, scale, area, and internal standard deviation. We also show that the curve smoothing, implicit in all vectorization methods, can be performed by the shape-preserving affine scale space. We extend this flow to a network of curves and give a sufficient condition for the topological preservation of the segmentation. The general vectorization method that follows from this analysis shows explainable behaviors, explicitly controlled by a few intuitive parameters. It is experimentally compared to state-of-the-art software and proved to have comparable or superior fidelity and cost efficiency.

Image Vectorization with Depth: convexified shape layers with depth ordering

Image vectorization is a process to convert a raster image into a scalable vector graphic format. Objective is to effectively remove the pixelization effect while representing boundaries of image by scaleable parameterized curves. We propose new image vectorization with depth which considers depth ordering among shapes and use curvature-based inpainting for convexifying shapes in vectorization process.From a given color quantized raster image, we first define each connected component of the same color as a shape layer, and construct depth ordering among them using a newly proposed depth ordering energy. Global depth ordering among all shapes is described by a directed graph, and we propose an energy to remove cycle within the graph. After constructing depth ordering of shapes, we convexify occluded regions by Euler's elastica curvature-based variational inpainting, and leverage on the stability of Modica-Mortola double-well potential energy to inpaint large regions. This is following human vision perception that boundaries of shapes extend smoothly, and we assume shapes are likely to be convex. Finally, we fit B\'{e}zier curves to the boundaries and save vectorization as a SVG file which allows superposition of curvature-based inpainted shapes following the depth ordering. This is a new way to vectorize images, by decomposing an image into scalable shape layers with computed depth ordering. This approach makes editing shapes and images more natural and intuitive. We also consider grouping shape layers for semantic vectorization. We present various numerical results and comparisons against recent layer-based vectorization methods to validate the proposed model.

Texture Edge detection by Patch consensus (TEP)

We propose Texture Edge detection using Patch consensus (TEP) which is a training-free method to detect the boundary of texture. We propose a new simple way to identify the texture edge location, using the consensus of segmented local patch information. While on the boundary, even using local patch information, the distinction between textures are typically not clear, but using neighbor consensus give a clear idea of the boundary. We utilize local patch, and its response against neighboring regions, to emphasize the similarities and the differences across different textures. The step of segmentation of response further emphasizes the edge location, and the neighborhood voting gives consensus and stabilize the edge detection. We analyze texture as a stationary process to give insight into the patch width parameter verses the quality of edge detection. We derive the necessary condition for textures to be distinguished, and analyze the patch width with respect to the scale of textures. Various experiments are presented to validate the proposed model.

WeakIdent: Weak formulation for Identifying Differential Equations using Narrow-fit and Trimming

Data-driven identification of differential equations is an interesting but challenging problem, especially when the given data are corrupted by noise. When the governing differential equation is a linear combination of various differential terms, the identification problem can be formulated as solving a linear system, with the feature matrix consisting of linear and nonlinear terms multiplied by a coefficient vector. This product is equal to the time derivative term, and thus generates dynamical behaviors. The goal is to identify the correct terms that form the equation to capture the dynamics of the given data. We propose a general and robust framework to recover differential equations using a weak formulation, for both ordinary and partial differential equations (ODEs and PDEs). The weak formulation facilitates an efficient and robust way to handle noise. For a robust recovery against noise and the choice of hyper-parameters, we introduce two new mechanisms, narrow-fit and trimming, for the coefficient support and value recovery, respectively. For each sparsity level, Subspace Pursuit is utilized to find an initial set of support from the large dictionary. Then, we focus on highly dynamic regions (rows of the feature matrix), and error normalize the feature matrix in the narrow-fit step. The support is further updated via trimming of the terms that contribute the least. Finally, the support set of features with the smallest Cross-Validation error is chosen as the result. A comprehensive set of numerical experiments are presented for both systems of ODEs and PDEs with various noise levels. The proposed method gives a robust recovery of the coefficients, and a significant denoising effect which can handle up to $100\%$ noise-to-signal ratio for some equations. We compare the proposed method with several state-of-the-art algorithms for the recovery of differential equations.

A Lifted $\ell_1 $ Framework for Sparse Recovery

Motivated by re-weighted $\ell_1$ approaches for sparse recovery, we propose a lifted $\ell_1$ (LL1) regularization which is a generalized form of several popular regularizations in the literature. By exploring such connections, we discover there are two types of lifting functions which can guarantee that the proposed approach is equivalent to the $\ell_0$ minimization. Computationally, we design an efficient algorithm via the alternating direction method of multiplier (ADMM) and establish the convergence for an unconstrained formulation. Experimental results are presented to demonstrate how this generalization improves sparse recovery over the state-of-the-art.

Counting Objects by Diffused Index: geometry-free and training-free approach

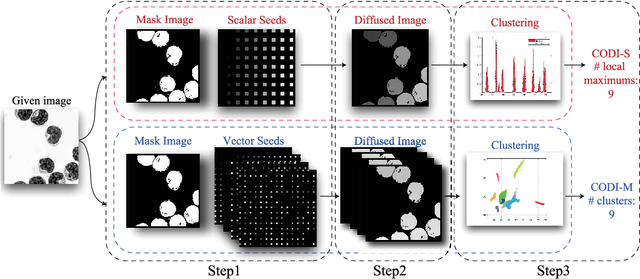
Counting objects is a fundamental but challenging problem. In this paper, we propose diffusion-based, geometry-free, and learning-free methodologies to count the number of objects in images. The main idea is to represent each object by a unique index value regardless of its intensity or size, and to simply count the number of index values. First, we place different vectors, refer to as seed vectors, uniformly throughout the mask image. The mask image has boundary information of the objects to be counted. Secondly, the seeds are diffused using an edge-weighted harmonic variational optimization model within each object. We propose an efficient algorithm based on an operator splitting approach and alternating direction minimization method, and theoretical analysis of this algorithm is given. An optimal solution of the model is obtained when the distributed seeds are completely diffused such that there is a unique intensity within each object, which we refer to as an index. For computational efficiency, we stop the diffusion process before a full convergence, and propose to cluster these diffused index values. We refer to this approach as Counting Objects by Diffused Index (CODI). We explore scalar and multi-dimensional seed vectors. For Scalar seeds, we use Gaussian fitting in histogram to count, while for vector seeds, we exploit a high-dimensional clustering method for the final step of counting via clustering. The proposed method is flexible even if the boundary of the object is not clear nor fully enclosed. We present counting results in various applications such as biological cells, agriculture, concert crowd, and transportation. Some comparisons with existing methods are presented.

A New Parallel Adaptive Clustering and its Application to Streaming Data

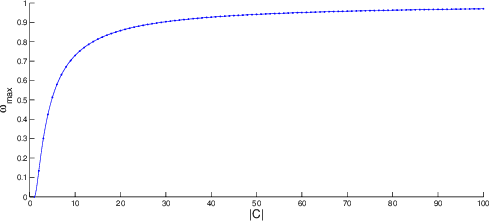
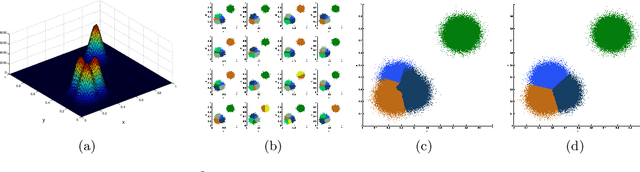
This paper presents a parallel adaptive clustering (PAC) algorithm to automatically classify data while simultaneously choosing a suitable number of classes. Clustering is an important tool for data analysis and understanding in a broad set of areas including data reduction, pattern analysis, and classification. However, the requirement to specify the number of clusters in advance and the computational burden associated with clustering large sets of data persist as challenges in clustering. We propose a new parallel adaptive clustering (PAC) algorithm that addresses these challenges by adaptively computing the number of clusters and leveraging the power of parallel computing. The algorithm clusters disjoint subsets of the data on parallel computation threads. We develop regularized set \mi{k}-means to efficiently cluster the results from the parallel threads. A refinement step further improves the clusters. The PAC algorithm offers the capability to adaptively cluster data sets which change over time by reusing the information from previous time steps to decrease computation. We provide theoretical analysis and numerical experiments to characterize the performance of the method, validate its properties, and demonstrate the computational efficiency of the method.

Curvature Regularized Surface Reconstruction from Point Cloud

We propose a variational functional and fast algorithms to reconstruct implicit surface from point cloud data with a curvature constraint. The minimizing functional balances the distance function from the point cloud and the mean curvature term. Only the point location is used, without any local normal or curvature estimation at each point. With the added curvature constraint, the computation becomes particularly challenging. To enhance the computational efficiency, we solve the problem by a novel operator splitting scheme. It replaces the original high-order PDEs by a decoupled PDE system, which is solved by a semi-implicit method. We also discuss approach using an augmented Lagrangian method. The proposed method shows robustness against noise, and recovers concave features and sharp corners better compared to models without curvature constraint. Numerical experiments in two and three dimensional data sets, noisy and sparse data are presented to validate the model.

Lattice Identification and Separation: Theory and Algorithm

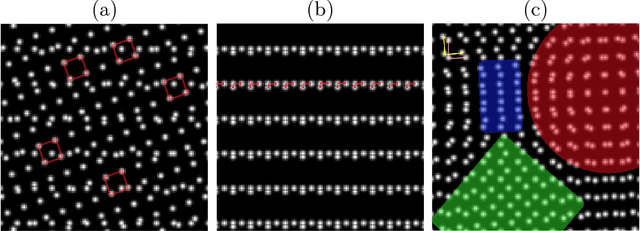
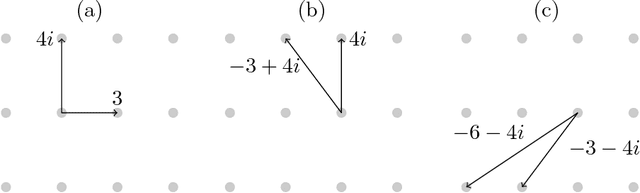
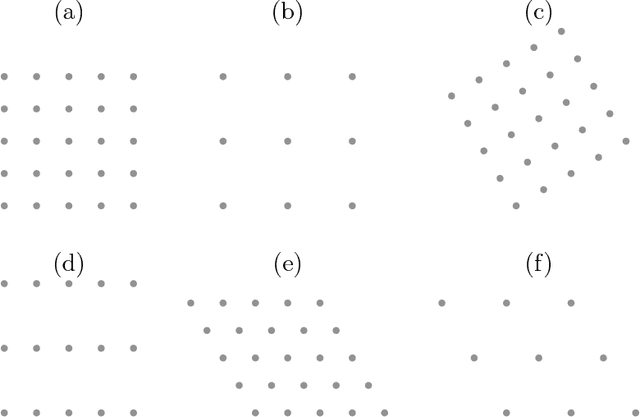
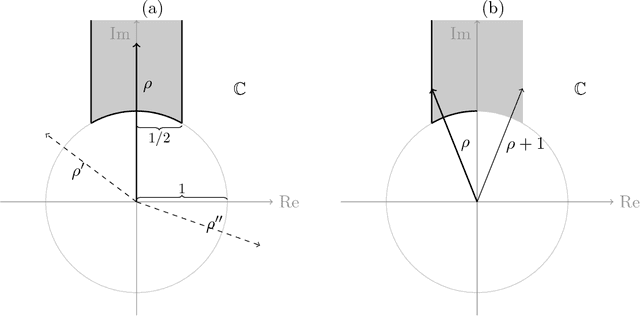
Motivated by lattice mixture identification and grain boundary detection, we present a framework for lattice pattern representation and comparison, and propose an efficient algorithm for lattice separation. We define new scale and shape descriptors, which helps to considerably reduce the size of equivalence classes of lattice bases. These finitely many equivalence relations are fully characterized by modular group theory. We construct the lattice space $\mathscr{L}$ based on the equivalent descriptors and define a metric $d_{\mathscr{L}}$ to accurately quantify the visual similarities and differences between lattices. Furthermore, we introduce the Lattice Identification and Separation Algorithm (LISA), which identifies each lattice patterns from superposed lattices. LISA finds lattice candidates from the high responses in the image spectrum, then sequentially extracts different layers of lattice patterns one by one. Analyzing the frequency components, we reveal the intricate dependency of LISA's performances on particle radius, lattice density, and relative translations. Various numerical experiments are designed to show LISA's robustness against a large number of lattice layers, moir\'{e} patterns and missing particles.