Lattice Identification and Separation: Theory and Algorithm
Paper and Code
Dec 19, 2018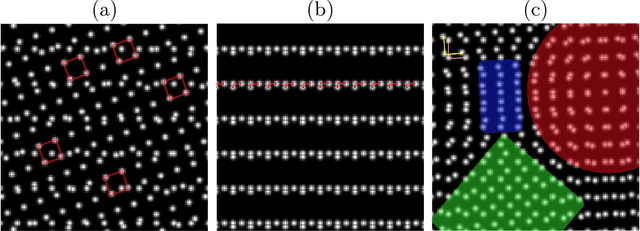
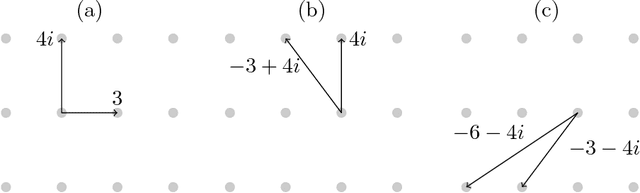
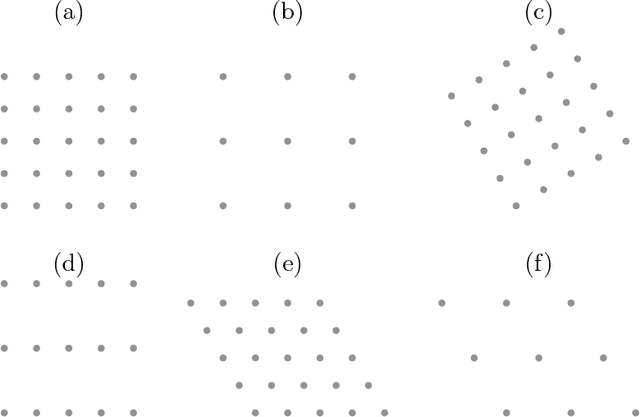
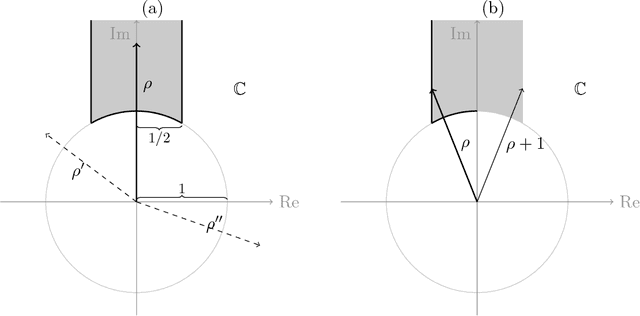
Motivated by lattice mixture identification and grain boundary detection, we present a framework for lattice pattern representation and comparison, and propose an efficient algorithm for lattice separation. We define new scale and shape descriptors, which helps to considerably reduce the size of equivalence classes of lattice bases. These finitely many equivalence relations are fully characterized by modular group theory. We construct the lattice space $\mathscr{L}$ based on the equivalent descriptors and define a metric $d_{\mathscr{L}}$ to accurately quantify the visual similarities and differences between lattices. Furthermore, we introduce the Lattice Identification and Separation Algorithm (LISA), which identifies each lattice patterns from superposed lattices. LISA finds lattice candidates from the high responses in the image spectrum, then sequentially extracts different layers of lattice patterns one by one. Analyzing the frequency components, we reveal the intricate dependency of LISA's performances on particle radius, lattice density, and relative translations. Various numerical experiments are designed to show LISA's robustness against a large number of lattice layers, moir\'{e} patterns and missing particles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge