WeakIdent: Weak formulation for Identifying Differential Equations using Narrow-fit and Trimming

Data-driven identification of differential equations is an interesting but challenging problem, especially when the given data are corrupted by noise. When the governing differential equation is a linear combination of various differential terms, the identification problem can be formulated as solving a linear system, with the feature matrix consisting of linear and nonlinear terms multiplied by a coefficient vector. This product is equal to the time derivative term, and thus generates dynamical behaviors. The goal is to identify the correct terms that form the equation to capture the dynamics of the given data. We propose a general and robust framework to recover differential equations using a weak formulation, for both ordinary and partial differential equations (ODEs and PDEs). The weak formulation facilitates an efficient and robust way to handle noise. For a robust recovery against noise and the choice of hyper-parameters, we introduce two new mechanisms, narrow-fit and trimming, for the coefficient support and value recovery, respectively. For each sparsity level, Subspace Pursuit is utilized to find an initial set of support from the large dictionary. Then, we focus on highly dynamic regions (rows of the feature matrix), and error normalize the feature matrix in the narrow-fit step. The support is further updated via trimming of the terms that contribute the least. Finally, the support set of features with the smallest Cross-Validation error is chosen as the result. A comprehensive set of numerical experiments are presented for both systems of ODEs and PDEs with various noise levels. The proposed method gives a robust recovery of the coefficients, and a significant denoising effect which can handle up to $100\%$ noise-to-signal ratio for some equations. We compare the proposed method with several state-of-the-art algorithms for the recovery of differential equations.

Counting Objects by Diffused Index: geometry-free and training-free approach

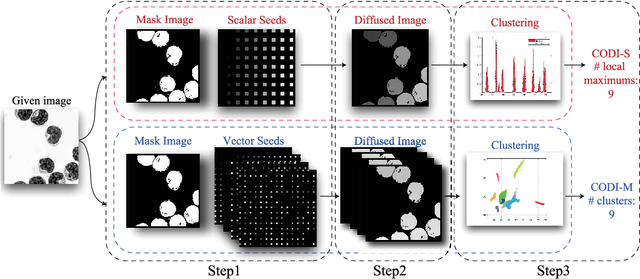
Counting objects is a fundamental but challenging problem. In this paper, we propose diffusion-based, geometry-free, and learning-free methodologies to count the number of objects in images. The main idea is to represent each object by a unique index value regardless of its intensity or size, and to simply count the number of index values. First, we place different vectors, refer to as seed vectors, uniformly throughout the mask image. The mask image has boundary information of the objects to be counted. Secondly, the seeds are diffused using an edge-weighted harmonic variational optimization model within each object. We propose an efficient algorithm based on an operator splitting approach and alternating direction minimization method, and theoretical analysis of this algorithm is given. An optimal solution of the model is obtained when the distributed seeds are completely diffused such that there is a unique intensity within each object, which we refer to as an index. For computational efficiency, we stop the diffusion process before a full convergence, and propose to cluster these diffused index values. We refer to this approach as Counting Objects by Diffused Index (CODI). We explore scalar and multi-dimensional seed vectors. For Scalar seeds, we use Gaussian fitting in histogram to count, while for vector seeds, we exploit a high-dimensional clustering method for the final step of counting via clustering. The proposed method is flexible even if the boundary of the object is not clear nor fully enclosed. We present counting results in various applications such as biological cells, agriculture, concert crowd, and transportation. Some comparisons with existing methods are presented.