Local Clustering for Lung Cancer Image Classification via Sparse Solution Technique

In this work, we propose to use a local clustering approach based on the sparse solution technique to study the medical image, especially the lung cancer image classification task. We view images as the vertices in a weighted graph and the similarity between a pair of images as the edges in the graph. The vertices within the same cluster can be assumed to share similar features and properties, thus making the applications of graph clustering techniques very useful for image classification. Recently, the approach based on the sparse solutions of linear systems for graph clustering has been found to identify clusters more efficiently than traditional clustering methods such as spectral clustering. We propose to use the two newly developed local clustering methods based on sparse solution of linear system for image classification. In addition, we employ a box spline-based tight-wavelet-framelet method to clean these images and help build a better adjacency matrix before clustering. The performance of our methods is shown to be very effective in classifying images. Our approach is significantly more efficient and either favorable or equally effective compared with other state-of-the-art approaches. Finally, we shall make a remark by pointing out two image deformation methods to build up more artificial image data to increase the number of labeled images.

Tree-based Ensemble Learning for Out-of-distribution Detection

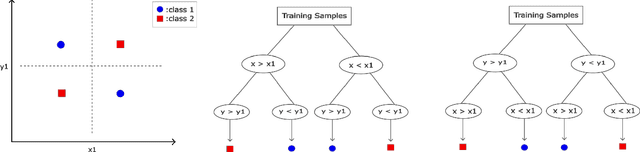
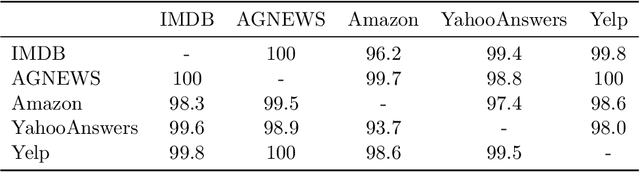
Being able to successfully determine whether the testing samples has similar distribution as the training samples is a fundamental question to address before we can safely deploy most of the machine learning models into practice. In this paper, we propose TOOD detection, a simple yet effective tree-based out-of-distribution (TOOD) detection mechanism to determine if a set of unseen samples will have similar distribution as of the training samples. The TOOD detection mechanism is based on computing pairwise hamming distance of testing samples' tree embeddings, which are obtained by fitting a tree-based ensemble model through in-distribution training samples. Our approach is interpretable and robust for its tree-based nature. Furthermore, our approach is efficient, flexible to various machine learning tasks, and can be easily generalized to unsupervised setting. Extensive experiments are conducted to show the proposed method outperforms other state-of-the-art out-of-distribution detection methods in distinguishing the in-distribution from out-of-distribution on various tabular, image, and text data.

Maximal Volume Matrix Cross Approximation for Image Compression and Least Squares Solution

We study the classic cross approximation of matrices based on the maximal volume submatrices. Our main results consist of an improvement of a classic estimate for matrix cross approximation and a greedy approach for finding the maximal volume submatrices. Indeed, we present a new proof of a classic estimate of the inequality with an improved constant. Also, we present a family of greedy maximal volume algorithms which improve the error bound of cross approximation of a matrix in the Chebyshev norm and also improve the computational efficiency of classic maximal volume algorithm. The proposed algorithms are shown to have theoretical guarantees of convergence. Finally, we present two applications: one is image compression and the other is least squares approximation of continuous functions. Our numerical results in the end of the paper demonstrate the effective performances of our approach.

Semi-supervised Local Cluster Extraction by Compressive Sensing

Local clustering problem aims at extracting a small local structure inside a graph without the necessity of knowing the entire graph structure. As the local structure is usually small in size compared to the entire graph, one can think of it as a compressive sensing problem where the indices of target cluster can be thought as a sparse solution to a linear system. In this paper, we propose a new semi-supervised local cluster extraction approach by applying the idea of compressive sensing based on two pioneering works under the same framework. Our approves improves the existing works by making the initial cut to be the entire graph and hence overcomes a major limitation of existing works, which is the low quality of initial cut. Extensive experimental results on multiple benchmark datasets demonstrate the effectiveness of our approach.

A Least Square Approach to Semi-supervised Local Cluster Extraction

A least square semi-supervised local clustering algorithm based on the idea of compressed sensing are proposed to extract clusters from a graph with known adjacency matrix. The algorithm is based on a two stage approaches similar to the one in \cite{LaiMckenzie2020}. However, under a weaker assumption and with less computational complexity than the one in \cite{LaiMckenzie2020}, the algorithm is shown to be able to find a desired cluster with high probability. Several numerical experiments including the synthetic data and real data such as MNIST, AT\&T and YaleB human faces data sets are conducted to demonstrate the performance of our algorithm.

A Compressive Sensing Approach to Community Detection with Applications

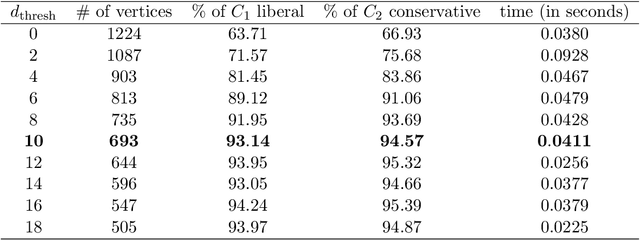
The community detection problem for graphs asks one to partition the n vertices V of a graph G into k communities, or clusters, such that there are many intracluster edges and few intercluster edges. Of course this is equivalent to finding a permutation matrix P such that, if A denotes the adjacency matrix of G, then PAP^T is approximately block diagonal. As there are k^n possible partitions of n vertices into k subsets, directly determining the optimal clustering is clearly infeasible. Instead one seeks to solve a more tractable approximation to the clustering problem. In this paper we reformulate the community detection problem via sparse solution of a linear system associated with the Laplacian of a graph G and then develop a two-stage approach based on a thresholding technique and a compressive sensing algorithm to find a sparse solution which corresponds to the community containing a vertex of interest in G. Crucially, our approach results in an algorithm which is able to find a single cluster of size n_0 in O(nlog(n)n_0) operations and all k clusters in fewer than O(n^2ln(n)) operations. This is a marked improvement over the classic spectral clustering algorithm, which is unable to find a single cluster at a time and takes approximately O(n^3) operations to find all k clusters. Moreover, we are able to provide robust guarantees of success for the case where G is drawn at random from the Stochastic Block Model, a popular model for graphs with clusters. Extensive numerical results are also provided, showing the efficacy of our algorithm on both synthetic and real-world data sets.

Stochastic Coordinate Coding and Its Application for Drosophila Gene Expression Pattern Annotation

\textit{Drosophila melanogaster} has been established as a model organism for investigating the fundamental principles of developmental gene interactions. The gene expression patterns of \textit{Drosophila melanogaster} can be documented as digital images, which are annotated with anatomical ontology terms to facilitate pattern discovery and comparison. The automated annotation of gene expression pattern images has received increasing attention due to the recent expansion of the image database. The effectiveness of gene expression pattern annotation relies on the quality of feature representation. Previous studies have demonstrated that sparse coding is effective for extracting features from gene expression images. However, solving sparse coding remains a computationally challenging problem, especially when dealing with large-scale data sets and learning large size dictionaries. In this paper, we propose a novel algorithm to solve the sparse coding problem, called Stochastic Coordinate Coding (SCC). The proposed algorithm alternatively updates the sparse codes via just a few steps of coordinate descent and updates the dictionary via second order stochastic gradient descent. The computational cost is further reduced by focusing on the non-zero components of the sparse codes and the corresponding columns of the dictionary only in the updating procedure. Thus, the proposed algorithm significantly improves the efficiency and the scalability, making sparse coding applicable for large-scale data sets and large dictionary sizes. Our experiments on Drosophila gene expression data sets demonstrate the efficiency and the effectiveness of the proposed algorithm.

Orthogonal Rank-One Matrix Pursuit for Low Rank Matrix Completion

In this paper, we propose an efficient and scalable low rank matrix completion algorithm. The key idea is to extend orthogonal matching pursuit method from the vector case to the matrix case. We further propose an economic version of our algorithm by introducing a novel weight updating rule to reduce the time and storage complexity. Both versions are computationally inexpensive for each matrix pursuit iteration, and find satisfactory results in a few iterations. Another advantage of our proposed algorithm is that it has only one tunable parameter, which is the rank. It is easy to understand and to use by the user. This becomes especially important in large-scale learning problems. In addition, we rigorously show that both versions achieve a linear convergence rate, which is significantly better than the previous known results. We also empirically compare the proposed algorithms with several state-of-the-art matrix completion algorithms on many real-world datasets, including the large-scale recommendation dataset Netflix as well as the MovieLens datasets. Numerical results show that our proposed algorithm is more efficient than competing algorithms while achieving similar or better prediction performance.