Who killed Lilly Kane? A case study in applying knowledge graphs to crime fiction

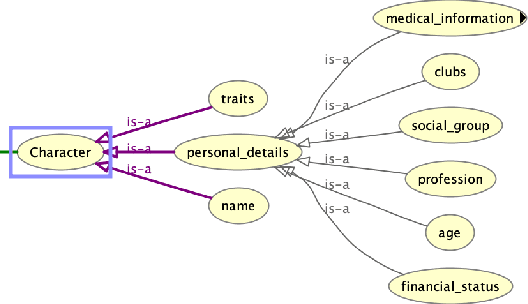
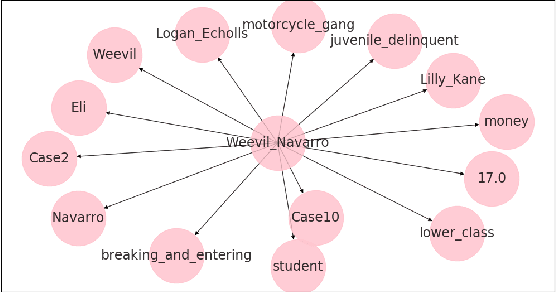
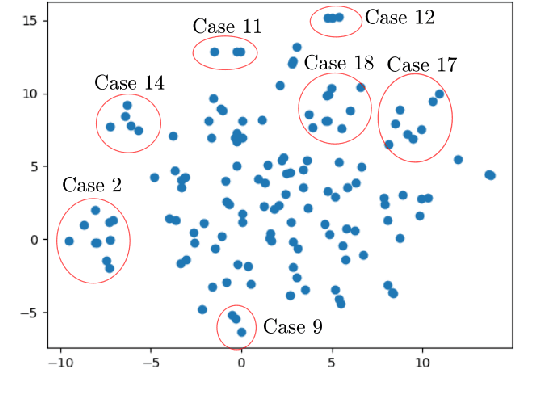
We present a preliminary study of a knowledge graph created from season one of the television show Veronica Mars, which follows the eponymous young private investigator as she attempts to solve the murder of her best friend Lilly Kane. We discuss various techniques for mining the knowledge graph for clues and potential suspects. We also discuss best practice for collaboratively constructing knowledge graphs from television shows.

SCOBO: Sparsity-Aware Comparison Oracle Based Optimization

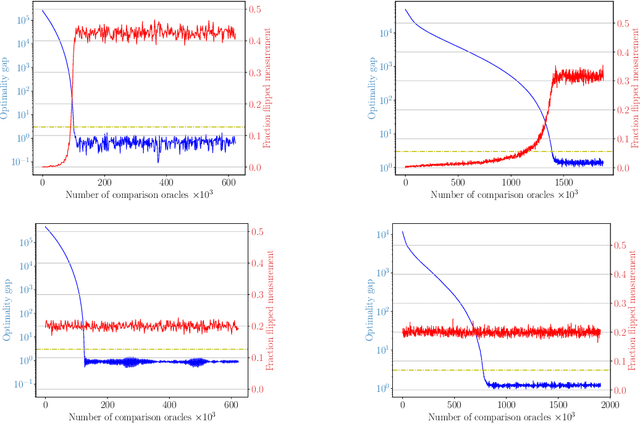
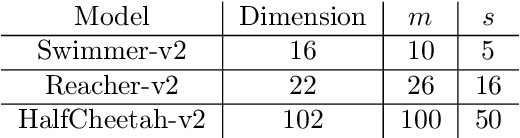
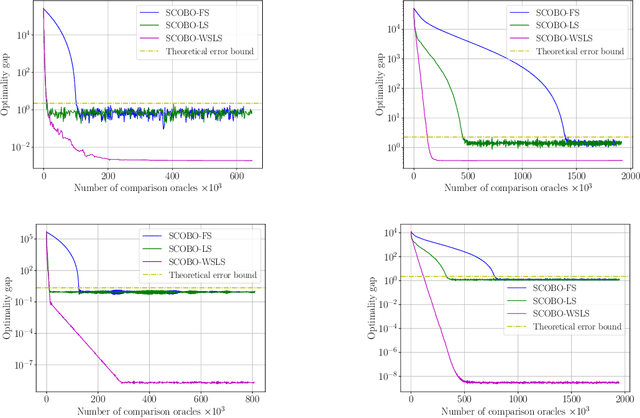
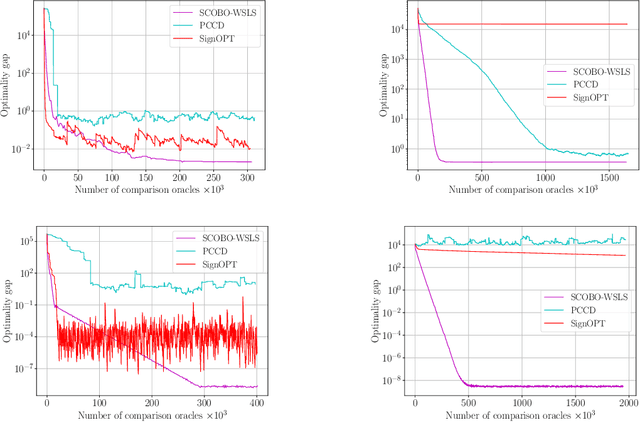
We study derivative-free optimization for convex functions where we further assume that function evaluations are unavailable. Instead, one only has access to a comparison oracle, which, given two points $x$ and $y$, and returns a single bit of information indicating which point has larger function value, $f(x)$ or $f(y)$, with some probability of being incorrect. This probability may be constant or it may depend on $|f(x)-f(y)|$. Previous algorithms for this problem have been hampered by a query complexity which is polynomially dependent on the problem dimension, $d$. We propose a novel algorithm that breaks this dependence: it has query complexity only logarithmically dependent on $d$ if the function in addition has low dimensional structure that can be exploited. Numerical experiments on synthetic data and the MuJoCo dataset show that our algorithm outperforms state-of-the-art methods for comparison based optimization, and is even competitive with other derivative-free algorithms that require explicit function evaluations.

Zeroth-Order Regularized Optimization (ZORO): Approximately Sparse Gradients and Adaptive Sampling

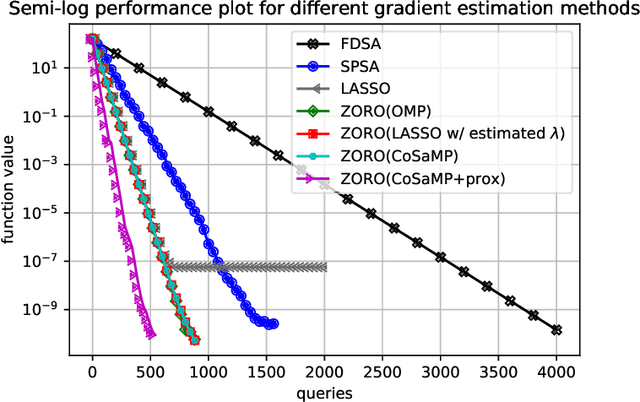
We consider the problem of minimizing a high-dimensional objective function, which may include a regularization term, using (possibly noisy) evaluations of the function. Such optimization is also called derivative-free, zeroth-order, or black-box optimization. We propose a new $\textbf{Z}$eroth-$\textbf{O}$rder $\textbf{R}$egularized $\textbf{O}$ptimization method, dubbed ZORO. When the underlying gradient is approximately sparse at an iterate, ZORO needs very few objective function evaluations to obtain a new iterate that decreases the objective function. We achieve this with an adaptive, randomized gradient estimator, followed by an inexact proximal-gradient scheme. Under a novel approximately sparse gradient assumption and various different convex settings, we show the (theoretical and empirical) convergence rate of ZORO is only logarithmically dependent on the problem dimension. Numerical experiments show that ZORO outperforms the existing methods with similar assumptions, on both synthetic and real datasets.

Power Weighted Shortest Paths for Unsupervised Learning

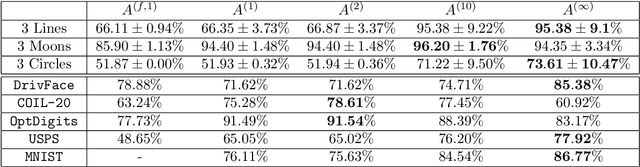
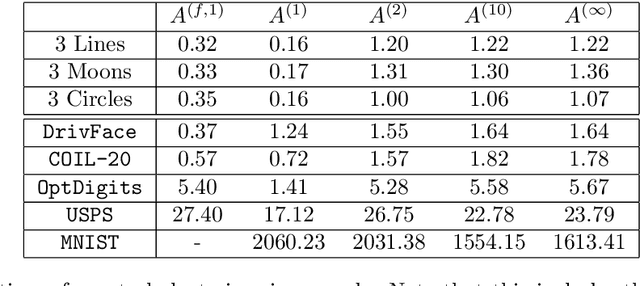
We study the use of power weighted shortest path distance functions for clustering high dimensional Euclidean data, under the assumption that the data is drawn from a collection of disjoint low dimensional manifolds. We argue, theoretically and experimentally, that this leads to higher clustering accuracy. We also present a fast algorithm for computing these distances.

A Compressive Sensing Approach to Community Detection with Applications

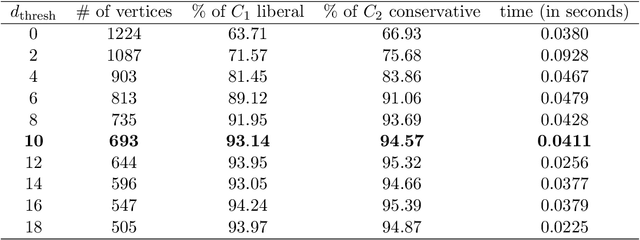
The community detection problem for graphs asks one to partition the n vertices V of a graph G into k communities, or clusters, such that there are many intracluster edges and few intercluster edges. Of course this is equivalent to finding a permutation matrix P such that, if A denotes the adjacency matrix of G, then PAP^T is approximately block diagonal. As there are k^n possible partitions of n vertices into k subsets, directly determining the optimal clustering is clearly infeasible. Instead one seeks to solve a more tractable approximation to the clustering problem. In this paper we reformulate the community detection problem via sparse solution of a linear system associated with the Laplacian of a graph G and then develop a two-stage approach based on a thresholding technique and a compressive sensing algorithm to find a sparse solution which corresponds to the community containing a vertex of interest in G. Crucially, our approach results in an algorithm which is able to find a single cluster of size n_0 in O(nlog(n)n_0) operations and all k clusters in fewer than O(n^2ln(n)) operations. This is a marked improvement over the classic spectral clustering algorithm, which is unable to find a single cluster at a time and takes approximately O(n^3) operations to find all k clusters. Moreover, we are able to provide robust guarantees of success for the case where G is drawn at random from the Stochastic Block Model, a popular model for graphs with clusters. Extensive numerical results are also provided, showing the efficacy of our algorithm on both synthetic and real-world data sets.