A first-order method for nonconvex-nonconcave minimax problems under a local Kurdyka-Łojasiewicz condition

We study a class of nonconvex-nonconcave minimax problems in which the inner maximization problem satisfies a local Kurdyka-{\L}ojasiewicz (KL) condition that may vary with the outer minimization variable. In contrast to the global KL or Polyak-{\L}ojasiewicz (PL) conditions commonly assumed in the literature -- which are significantly stronger and often too restrictive in practice -- this local KL condition accommodates a broader range of practical scenarios. However, it also introduces new analytical challenges. In particular, as an optimization algorithm progresses toward a stationary point of the problem, the region over which the KL condition holds may shrink, resulting in a more intricate and potentially ill-conditioned landscape. To address this challenge, we show that the associated maximal function is locally H\"older smooth. Leveraging this key property, we develop an inexact proximal gradient method for solving the minimax problem, where the inexact gradient of the maximal function is computed by applying a proximal gradient method to a KL-structured subproblem. Under mild assumptions, we establish complexity guarantees for computing an approximate stationary point of the minimax problem.

First-order methods for stochastic and finite-sum convex optimization with deterministic constraints

In this paper, we study a class of stochastic and finite-sum convex optimization problems with deterministic constraints. Existing methods typically aim to find an $\epsilon$-$expectedly\ feasible\ stochastic\ optimal$ solution, in which the expected constraint violation and expected optimality gap are both within a prescribed tolerance $\epsilon$. However, in many practical applications, constraints must be nearly satisfied with certainty, rendering such solutions potentially unsuitable due to the risk of substantial violations. To address this issue, we propose stochastic first-order methods for finding an $\epsilon$-$surely\ feasible\ stochastic\ optimal$ ($\epsilon$-SFSO) solution, where the constraint violation is deterministically bounded by $\epsilon$ and the expected optimality gap is at most $\epsilon$. Our methods apply an accelerated stochastic gradient (ASG) scheme or a modified variance-reduced ASG scheme $only\ once$ to a sequence of quadratic penalty subproblems with appropriately chosen penalty parameters. We establish first-order oracle complexity bounds for the proposed methods in computing an $\epsilon$-SFSO solution. As a byproduct, we also derive first-order oracle complexity results for sample average approximation method in computing an $\epsilon$-SFSO solution of the stochastic optimization problem using our proposed methods to solve the sample average problem.

Complexity of normalized stochastic first-order methods with momentum under heavy-tailed noise

In this paper, we propose practical normalized stochastic first-order methods with Polyak momentum, multi-extrapolated momentum, and recursive momentum for solving unconstrained optimization problems. These methods employ dynamically updated algorithmic parameters and do not require explicit knowledge of problem-dependent quantities such as the Lipschitz constant or noise bound. We establish first-order oracle complexity results for finding approximate stochastic stationary points under heavy-tailed noise and weakly average smoothness conditions -- both of which are weaker than the commonly used bounded variance and mean-squared smoothness assumptions. Our complexity bounds either improve upon or match the best-known results in the literature. Numerical experiments are presented to demonstrate the practical effectiveness of the proposed methods.

Nested Stochastic Gradient Descent for (Generalized) Sinkhorn Distance-Regularized Distributionally Robust Optimization

Distributionally robust optimization (DRO) is a powerful technique to train robust models against data distribution shift. This paper aims to solve regularized nonconvex DRO problems, where the uncertainty set is modeled by a so-called generalized Sinkhorn distance and the loss function is nonconvex and possibly unbounded. Such a distance allows to model uncertainty of distributions with different probability supports and divergence functions. For this class of regularized DRO problems, we derive a novel dual formulation taking the form of nested stochastic programming, where the dual variable depends on the data sample. To solve the dual problem, we provide theoretical evidence to design a nested stochastic gradient descent (SGD) algorithm, which leverages stochastic approximation to estimate the nested stochastic gradients. We study the convergence rate of nested SGD and establish polynomial iteration and sample complexities that are independent of the data size and parameter dimension, indicating its potential for solving large-scale DRO problems. We conduct numerical experiments to demonstrate the efficiency and robustness of the proposed algorithm.

Variance-reduced first-order methods for deterministically constrained stochastic nonconvex optimization with strong convergence guarantees

In this paper, we study a class of deterministically constrained stochastic optimization problems. Existing methods typically aim to find an $\epsilon$-stochastic stationary point, where the expected violations of both constraints and first-order stationarity are within a prescribed accuracy $\epsilon$. However, in many practical applications, it is crucial that the constraints be nearly satisfied with certainty, making such an $\epsilon$-stochastic stationary point potentially undesirable due to the risk of significant constraint violations. To address this issue, we propose single-loop variance-reduced stochastic first-order methods, where the stochastic gradient of the stochastic component is computed using either a truncated recursive momentum scheme or a truncated Polyak momentum scheme for variance reduction, while the gradient of the deterministic component is computed exactly. Under the error bound condition with a parameter $\theta \geq 1$ and other suitable assumptions, we establish that the proposed methods achieve a sample complexity and first-order operation complexity of $\widetilde O(\epsilon^{-\max\{4, 2\theta\}})$ for finding a stronger $\epsilon$-stochastic stationary point, where the constraint violation is within $\epsilon$ with certainty, and the expected violation of first-order stationarity is within $\epsilon$. To the best of our knowledge, this is the first work to develop methods with provable complexity guarantees for finding an approximate stochastic stationary point of such problems that nearly satisfies all constraints with certainty.

Single-loop Stochastic Algorithms for Difference of Max-Structured Weakly Convex Functions

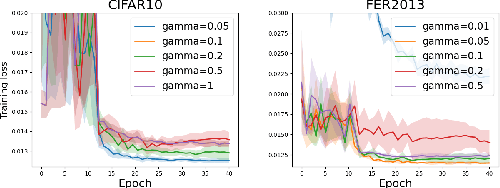
In this paper, we study a class of non-smooth non-convex problems in the form of $\min_{x}[\max_{y\in Y}\phi(x, y) - \max_{z\in Z}\psi(x, z)]$, where both $\Phi(x) = \max_{y\in Y}\phi(x, y)$ and $\Psi(x)=\max_{z\in Z}\psi(x, z)$ are weakly convex functions, and $\phi(x, y), \psi(x, z)$ are strongly concave functions in terms of $y$ and $z$, respectively. It covers two families of problems that have been studied but are missing single-loop stochastic algorithms, i.e., difference of weakly convex functions and weakly convex strongly-concave min-max problems. We propose a stochastic Moreau envelope approximate gradient method dubbed SMAG, the first single-loop algorithm for solving these problems, and provide a state-of-the-art non-asymptotic convergence rate. The key idea of the design is to compute an approximate gradient of the Moreau envelopes of $\Phi, \Psi$ using only one step of stochastic gradient update of the primal and dual variables. Empirically, we conduct experiments on positive-unlabeled (PU) learning and partial area under ROC curve (pAUC) optimization with an adversarial fairness regularizer to validate the effectiveness of our proposed algorithms.

Newton-CG methods for nonconvex unconstrained optimization with Hölder continuous Hessian

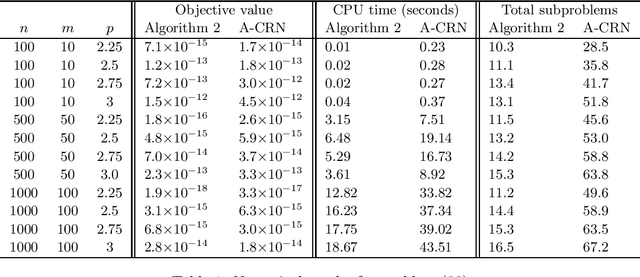
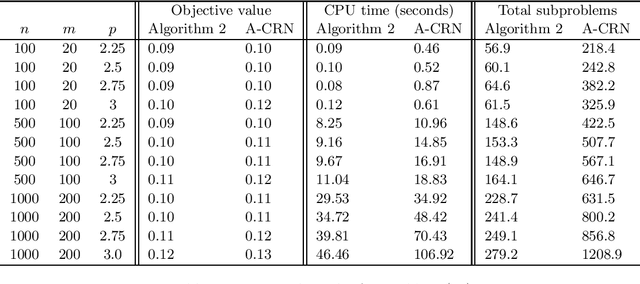
In this paper we consider a nonconvex unconstrained optimization problem minimizing a twice differentiable objective function with H\"older continuous Hessian. Specifically, we first propose a Newton-conjugate gradient (Newton-CG) method for finding an approximate first-order stationary point (FOSP) of this problem, assuming the associated the H\"older parameters are explicitly known. Then we develop a parameter-free Newton-CG method without requiring any prior knowledge of these parameters. To the best of our knowledge, this method is the first parameter-free second-order method achieving the best-known iteration and operation complexity for finding an approximate FOSP of this problem. Furthermore, we propose a Newton-CG method for finding an approximate second-order stationary point (SOSP) of the considered problem with high probability and establish its iteration and operation complexity. Finally, we present preliminary numerical results to demonstrate the superior practical performance of our parameter-free Newton-CG method over a well-known regularized Newton method.

A Newton-CG based barrier-augmented Lagrangian method for general nonconvex conic optimization

In this paper we consider finding an approximate second-order stationary point (SOSP) of general nonconvex conic optimization that minimizes a twice differentiable function subject to nonlinear equality constraints and also a convex conic constraint. In particular, we propose a Newton-conjugate gradient (Newton-CG) based barrier-augmented Lagrangian method for finding an approximate SOSP of this problem. Under some mild assumptions, we show that our method enjoys a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-11/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-11/2}\min\{n,\epsilon^{-5/4}\})$ for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of general nonconvex conic optimization with high probability. Moreover, under a constraint qualification, these complexity bounds are improved to $\widetilde{\cal O}(\epsilon^{-7/2})$ and $\widetilde{\cal O}(\epsilon^{-7/2}\min\{n,\epsilon^{-3/4}\})$, respectively. To the best of our knowledge, this is the first study on the complexity of finding an approximate SOSP of general nonconvex conic optimization. Preliminary numerical results are presented to demonstrate superiority of the proposed method over first-order methods in terms of solution quality.

A Newton-CG based augmented Lagrangian method for finding a second-order stationary point of nonconvex equality constrained optimization with complexity guarantees

In this paper we consider finding a second-order stationary point (SOSP) of nonconvex equality constrained optimization when a nearly feasible point is known. In particular, we first propose a new Newton-CG method for finding an approximate SOSP of unconstrained optimization and show that it enjoys a substantially better complexity than the Newton-CG method [56]. We then propose a Newton-CG based augmented Lagrangian (AL) method for finding an approximate SOSP of nonconvex equality constrained optimization, in which the proposed Newton-CG method is used as a subproblem solver. We show that under a generalized linear independence constraint qualification (GLICQ), our AL method enjoys a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-7/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-7/2}\min\{n,\epsilon^{-3/4}\})$ for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of nonconvex equality constrained optimization with high probability, which are significantly better than the ones achieved by the proximal AL method [60]. Besides, we show that it has a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-11/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-11/2}\min\{n,\epsilon^{-5/4}\})$ when the GLICQ does not hold. To the best of our knowledge, all the complexity results obtained in this paper are new for finding an approximate SOSP of nonconvex equality constrained optimization with high probability. Preliminary numerical results also demonstrate the superiority of our proposed methods over the ones in [56,60].

A first-order augmented Lagrangian method for constrained minimax optimization

In this paper we study a class of constrained minimax problems. In particular, we propose a first-order augmented Lagrangian method for solving them, whose subproblems turn out to be a much simpler structured minimax problem and are suitably solved by a first-order method recently developed in [26] by the authors. Under some suitable assumptions, an \emph{operation complexity} of ${\cal O}(\varepsilon^{-4}\log\varepsilon^{-1})$, measured by its fundamental operations, is established for the first-order augmented Lagrangian method for finding an $\varepsilon$-KKT solution of the constrained minimax problems.