Newton-CG methods for nonconvex unconstrained optimization with Hölder continuous Hessian

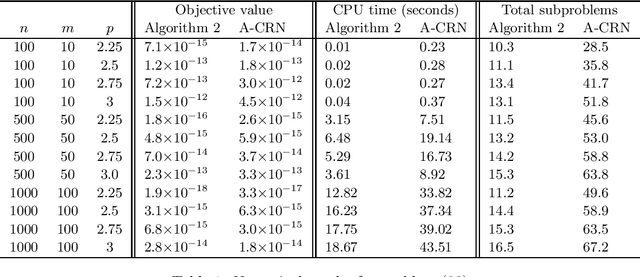
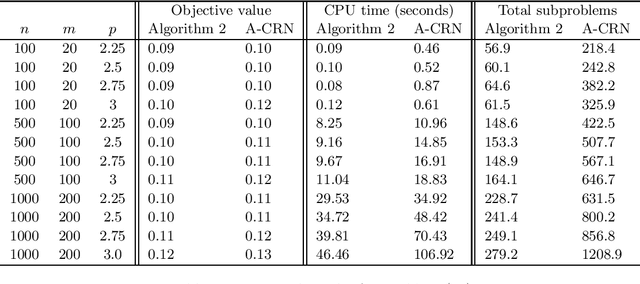
In this paper we consider a nonconvex unconstrained optimization problem minimizing a twice differentiable objective function with H\"older continuous Hessian. Specifically, we first propose a Newton-conjugate gradient (Newton-CG) method for finding an approximate first-order stationary point (FOSP) of this problem, assuming the associated the H\"older parameters are explicitly known. Then we develop a parameter-free Newton-CG method without requiring any prior knowledge of these parameters. To the best of our knowledge, this method is the first parameter-free second-order method achieving the best-known iteration and operation complexity for finding an approximate FOSP of this problem. Furthermore, we propose a Newton-CG method for finding an approximate second-order stationary point (SOSP) of the considered problem with high probability and establish its iteration and operation complexity. Finally, we present preliminary numerical results to demonstrate the superior practical performance of our parameter-free Newton-CG method over a well-known regularized Newton method.