Stochastic first-order methods with multi-extrapolated momentum for highly smooth unconstrained optimization

In this paper we consider an unconstrained stochastic optimization problem where the objective function exhibits a high order of smoothness. In particular, we propose a stochastic first-order method (SFOM) with multi-extrapolated momentum, in which multiple extrapolations are performed in each iteration, followed by a momentum step based on these extrapolations. We show that our proposed SFOM with multi-extrapolated momentum can accelerate optimization by exploiting the high-order smoothness of the objective function $f$. Specifically, assuming that the gradient and the $p$th-order derivative of $f$ are Lipschitz continuous for some $p\ge2$, and under some additional mild assumptions, we establish that our method achieves a sample complexity of $\widetilde{\mathcal{O}}(\epsilon^{-(3p+1)/p})$ for finding a point $x$ satisfying $\mathbb{E}[\|\nabla f(x)\|]\le\epsilon$. To the best of our knowledge, our method is the first SFOM to leverage arbitrary order smoothness of the objective function for acceleration, resulting in a sample complexity that strictly improves upon the best-known results without assuming the average smoothness condition. Finally, preliminary numerical experiments validate the practical performance of our method and corroborate our theoretical findings.

Stochastic interior-point methods for smooth conic optimization with applications

Conic optimization plays a crucial role in many machine learning (ML) problems. However, practical algorithms for conic constrained ML problems with large datasets are often limited to specific use cases, as stochastic algorithms for general conic optimization remain underdeveloped. To fill this gap, we introduce a stochastic interior-point method (SIPM) framework for general conic optimization, along with four novel SIPM variants leveraging distinct stochastic gradient estimators. Under mild assumptions, we establish the global convergence rates of our proposed SIPMs, which, up to a logarithmic factor, match the best-known rates in stochastic unconstrained optimization. Finally, our numerical experiments on robust linear regression, multi-task relationship learning, and clustering data streams demonstrate the effectiveness and efficiency of our approach.

Multi-Grained Preference Enhanced Transformer for Multi-Behavior Sequential Recommendation

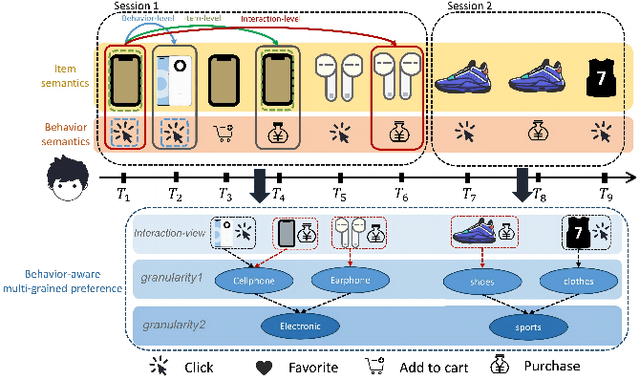
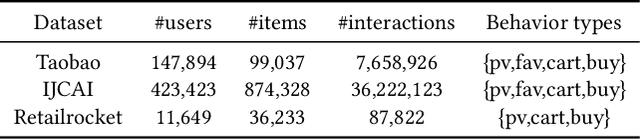
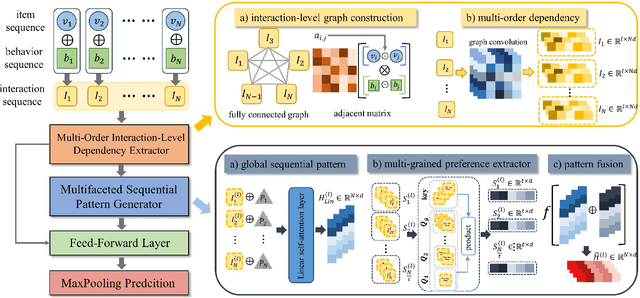
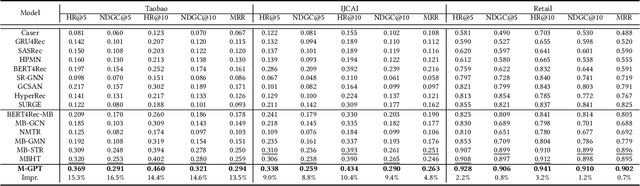
Sequential recommendation (SR) aims to predict the next purchasing item according to users' dynamic preference learned from their historical user-item interactions. To improve the performance of recommendation, learning dynamic heterogeneous cross-type behavior dependencies is indispensable for recommender system. However, there still exists some challenges in Multi-Behavior Sequential Recommendation (MBSR). On the one hand, existing methods only model heterogeneous multi-behavior dependencies at behavior-level or item-level, and modelling interaction-level dependencies is still a challenge. On the other hand, the dynamic multi-grained behavior-aware preference is hard to capture in interaction sequences, which reflects interaction-aware sequential pattern. To tackle these challenges, we propose a Multi-Grained Preference enhanced Transformer framework (M-GPT). First, M-GPT constructs a interaction-level graph of historical cross-typed interactions in a sequence. Then graph convolution is performed to derive interaction-level multi-behavior dependency representation repeatedly, in which the complex correlation between historical cross-typed interactions at specific orders can be well learned. Secondly, a novel multi-scale transformer architecture equipped with multi-grained user preference extraction is proposed to encode the interaction-aware sequential pattern enhanced by capturing temporal behavior-aware multi-grained preference . Experiments on the real-world datasets indicate that our method M-GPT consistently outperforms various state-of-the-art recommendation methods.

Newton-CG methods for nonconvex unconstrained optimization with Hölder continuous Hessian

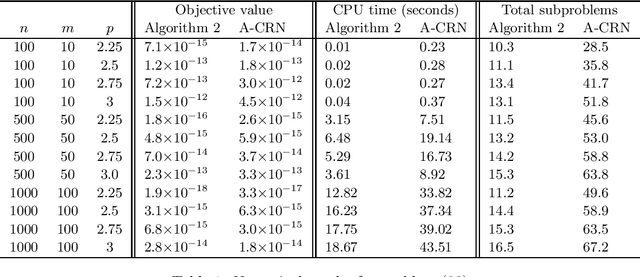
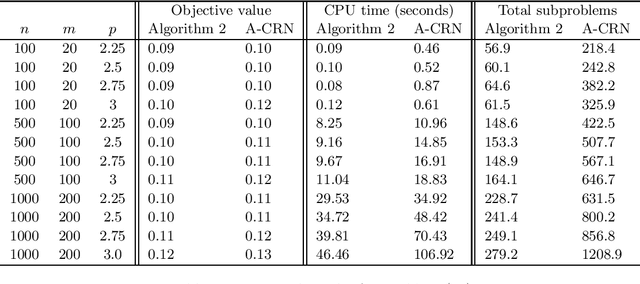
In this paper we consider a nonconvex unconstrained optimization problem minimizing a twice differentiable objective function with H\"older continuous Hessian. Specifically, we first propose a Newton-conjugate gradient (Newton-CG) method for finding an approximate first-order stationary point (FOSP) of this problem, assuming the associated the H\"older parameters are explicitly known. Then we develop a parameter-free Newton-CG method without requiring any prior knowledge of these parameters. To the best of our knowledge, this method is the first parameter-free second-order method achieving the best-known iteration and operation complexity for finding an approximate FOSP of this problem. Furthermore, we propose a Newton-CG method for finding an approximate second-order stationary point (SOSP) of the considered problem with high probability and establish its iteration and operation complexity. Finally, we present preliminary numerical results to demonstrate the superior practical performance of our parameter-free Newton-CG method over a well-known regularized Newton method.

A proximal augmented Lagrangian based algorithm for federated learning with global and local convex conic constraints

This paper considers federated learning (FL) with constraints, where the central server and all local clients collectively minimize a sum of convex local objective functions subject to global and local convex conic constraints. To train the model without moving local data from clients to the central server, we propose an FL framework in which each local client performs multiple updates using the local objective and local constraint, while the central server handles the global constraint and performs aggregation based on the updated local models. In particular, we develop a proximal augmented Lagrangian (AL) based algorithm for FL with global and local convex conic constraints. The subproblems arising in this algorithm are solved by an inexact alternating direction method of multipliers (ADMM) in a federated fashion. Under a local Lipschitz condition and mild assumptions, we establish the worst-case complexity bounds of the proposed algorithm for finding an approximate KKT solution. To the best of our knowledge, this work proposes the first algorithm for FL with global and local constraints. Our numerical experiments demonstrate the practical advantages of our algorithm in performing Neyman-Pearson classification and enhancing model fairness in the context of FL.

A Newton-CG based barrier-augmented Lagrangian method for general nonconvex conic optimization

In this paper we consider finding an approximate second-order stationary point (SOSP) of general nonconvex conic optimization that minimizes a twice differentiable function subject to nonlinear equality constraints and also a convex conic constraint. In particular, we propose a Newton-conjugate gradient (Newton-CG) based barrier-augmented Lagrangian method for finding an approximate SOSP of this problem. Under some mild assumptions, we show that our method enjoys a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-11/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-11/2}\min\{n,\epsilon^{-5/4}\})$ for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of general nonconvex conic optimization with high probability. Moreover, under a constraint qualification, these complexity bounds are improved to $\widetilde{\cal O}(\epsilon^{-7/2})$ and $\widetilde{\cal O}(\epsilon^{-7/2}\min\{n,\epsilon^{-3/4}\})$, respectively. To the best of our knowledge, this is the first study on the complexity of finding an approximate SOSP of general nonconvex conic optimization. Preliminary numerical results are presented to demonstrate superiority of the proposed method over first-order methods in terms of solution quality.

A Newton-CG based augmented Lagrangian method for finding a second-order stationary point of nonconvex equality constrained optimization with complexity guarantees

In this paper we consider finding a second-order stationary point (SOSP) of nonconvex equality constrained optimization when a nearly feasible point is known. In particular, we first propose a new Newton-CG method for finding an approximate SOSP of unconstrained optimization and show that it enjoys a substantially better complexity than the Newton-CG method [56]. We then propose a Newton-CG based augmented Lagrangian (AL) method for finding an approximate SOSP of nonconvex equality constrained optimization, in which the proposed Newton-CG method is used as a subproblem solver. We show that under a generalized linear independence constraint qualification (GLICQ), our AL method enjoys a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-7/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-7/2}\min\{n,\epsilon^{-3/4}\})$ for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of nonconvex equality constrained optimization with high probability, which are significantly better than the ones achieved by the proximal AL method [60]. Besides, we show that it has a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-11/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-11/2}\min\{n,\epsilon^{-5/4}\})$ when the GLICQ does not hold. To the best of our knowledge, all the complexity results obtained in this paper are new for finding an approximate SOSP of nonconvex equality constrained optimization with high probability. Preliminary numerical results also demonstrate the superiority of our proposed methods over the ones in [56,60].

A Newton-CG based barrier method for finding a second-order stationary point of nonconvex conic optimization with complexity guarantees

In this paper we consider finding an approximate second-order stationary point (SOSP) of nonconvex conic optimization that minimizes a twice differentiable function over the intersection of an affine subspace and a convex cone. In particular, we propose a Newton-conjugate gradient (Newton-CG) based barrier method for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of this problem. Our method is not only implementable, but also achieves an iteration complexity of ${\cal O}(\epsilon^{-3/2})$, which matches the best known iteration complexity of second-order methods for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of unconstrained nonconvex optimization. The operation complexity of $\widetilde{\cal O}(\epsilon^{-3/2}\min\{n,\epsilon^{-1/4}\})$, measured by the amount of fundamental operations, is also established for our method.