DeMuon: A Decentralized Muon for Matrix Optimization over Graphs

In this paper, we propose DeMuon, a method for decentralized matrix optimization over a given communication topology. DeMuon incorporates matrix orthogonalization via Newton-Schulz iterations-a technique inherited from its centralized predecessor, Muon-and employs gradient tracking to mitigate heterogeneity among local functions. Under heavy-tailed noise conditions and additional mild assumptions, we establish the iteration complexity of DeMuon for reaching an approximate stochastic stationary point. This complexity result matches the best-known complexity bounds of centralized algorithms in terms of dependence on the target tolerance. To the best of our knowledge, DeMuon is the first direct extension of Muon to decentralized optimization over graphs with provable complexity guarantees. We conduct preliminary numerical experiments on decentralized transformer pretraining over graphs with varying degrees of connectivity. Our numerical results demonstrate a clear margin of improvement of DeMuon over other popular decentralized algorithms across different network topologies.

A Linear Time Algorithm for the Optimal Discrete IRS Beamforming

It remains an open problem to find the optimal configuration of phase shifts under the discrete constraint for intelligent reflecting surface (IRS) in polynomial time. The above problem is widely believed to be difficult because it is not linked to any known combinatorial problems that can be solved efficiently. The branch-and-bound algorithms and the approximation algorithms constitute the best results in this area. Nevertheless, this work shows that the global optimum can actually be reached in linear time in terms of the number of reflective elements (REs) of IRS. The main idea is to geometrically interpret the discrete beamforming problem as choosing the optimal point on the unit circle. Although the number of possible combinations of phase shifts grows exponentially with the number of REs, it turns out that there are merely a linear number of points on the unit circle to consider. Furthermore, the proposed algorithm can be viewed as a novel approach to a special case of the discrete quadratic program (QP).

Configuring Intelligent Reflecting Surface with Performance Guarantees: Optimal Beamforming

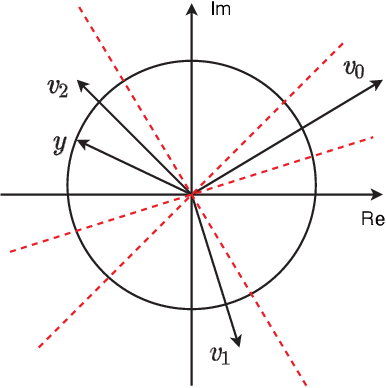
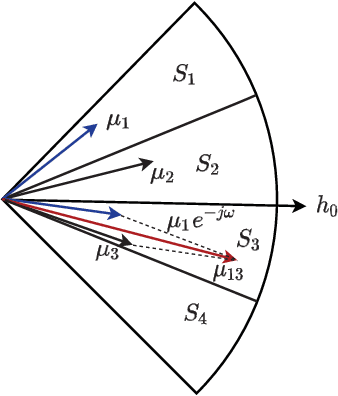
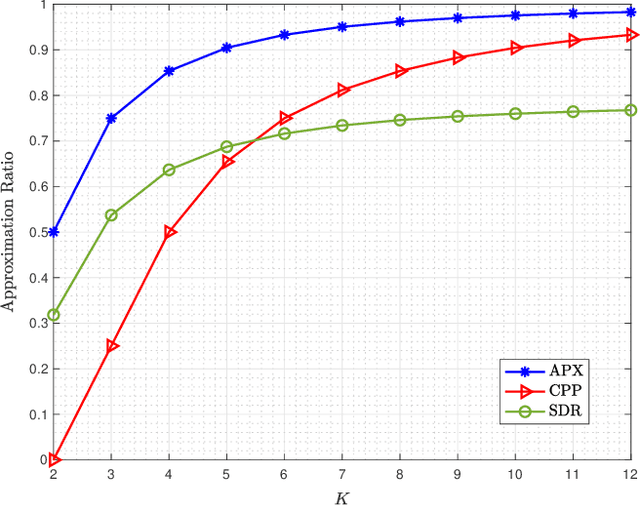
This work proposes linear time strategies to optimally configure the phase shifts for the reflective elements of an intelligent reflecting surface (IRS). Specifically, we show that the binary phase beamforming can be optimally solved in linear time to maximize the received signal-to-noise ratio (SNR). For the general K-ary phase beamforming, we develop a linear time approximation algorithm that guarantees performance within a constant fraction (1+\cos(\pi/K))/2 of the global optimum, e.g., it can attain over 85% of the optimal performance for the quadrature beamforming with K=4. According to the numerical results, the proposed approximation algorithm for discrete IRS beamforming outperforms the existing algorithms significantly in boosting the received SNR.