$XX^{t}$ Can Be Faster

We present a new algorithm RXTX that computes product of matrix by its transpose $XX^{t}$. RXTX uses $5\%$ less multiplications and additions than State-of-the-Art and achieves accelerations even for small sizes of matrix $X$. The algorithm was discovered by combining Machine Learning-based search methods with Combinatorial Optimization.

Zeroth-Order Optimization Meets Human Feedback: Provable Learning via Ranking Oracles

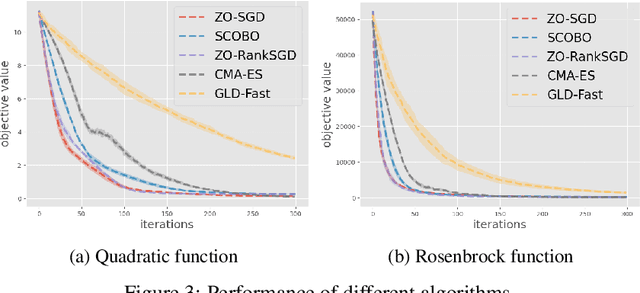
In this paper, we focus on a novel optimization problem in which the objective function is a black-box and can only be evaluated through a ranking oracle. This problem is common in real-world applications, particularly in cases where the function is assessed by human judges. Reinforcement Learning with Human Feedback (RLHF) is a prominent example of such an application, which is adopted by the recent works \cite{ouyang2022training,liu2023languages,chatgpt,bai2022training} to improve the quality of Large Language Models (LLMs) with human guidance. We propose ZO-RankSGD, a first-of-its-kind zeroth-order optimization algorithm, to solve this optimization problem with a theoretical guarantee. Specifically, our algorithm employs a new rank-based random estimator for the descent direction and is proven to converge to a stationary point. ZO-RankSGD can also be directly applied to the policy search problem in reinforcement learning when only a ranking oracle of the episode reward is available. This makes ZO-RankSGD a promising alternative to existing RLHF methods, as it optimizes in an online fashion and thus can work without any pre-collected data. Furthermore, we demonstrate the effectiveness of ZO-RankSGD in a novel application: improving the quality of images generated by a diffusion generative model with human ranking feedback. Throughout experiments, we found that ZO-RankSGD can significantly enhance the detail of generated images with only a few rounds of human feedback. Overall, our work advances the field of zeroth-order optimization by addressing the problem of optimizing functions with only ranking feedback, and offers an effective approach for aligning human and machine intentions in a wide range of domains. Our code is released here \url{https://github.com/TZW1998/Taming-Stable-Diffusion-with-Human-Ranking-Feedback}.

Invariant Layers for Graphs with Nodes of Different Types

Neural networks that satisfy invariance with respect to input permutations have been widely studied in machine learning literature. However, in many applications, only a subset of all input permutations is of interest. For heterogeneous graph data, one can focus on permutations that preserve node types. We fully characterize linear layers invariant to such permutations. We verify experimentally that implementing these layers in graph neural network architectures allows learning important node interactions more effectively than existing techniques. We show that the dimension of space of these layers is given by a generalization of Bell numbers, extending the work (Maron et al., 2019). We further narrow the invariant network design space by addressing a question about the sizes of tensor layers necessary for function approximation on graph data. Our findings suggest that function approximation on a graph with $n$ nodes can be done with tensors of sizes $\leq n$, which is tighter than the best-known bound $\leq n(n-1)/2$. For $d \times d$ image data with translation symmetry, our methods give a tight upper bound $2d - 1$ (instead of $d^{4}$) on sizes of invariant tensor generators via a surprising connection to Davenport constants.

A Linear Time Algorithm for the Optimal Discrete IRS Beamforming

It remains an open problem to find the optimal configuration of phase shifts under the discrete constraint for intelligent reflecting surface (IRS) in polynomial time. The above problem is widely believed to be difficult because it is not linked to any known combinatorial problems that can be solved efficiently. The branch-and-bound algorithms and the approximation algorithms constitute the best results in this area. Nevertheless, this work shows that the global optimum can actually be reached in linear time in terms of the number of reflective elements (REs) of IRS. The main idea is to geometrically interpret the discrete beamforming problem as choosing the optimal point on the unit circle. Although the number of possible combinations of phase shifts grows exponentially with the number of REs, it turns out that there are merely a linear number of points on the unit circle to consider. Furthermore, the proposed algorithm can be viewed as a novel approach to a special case of the discrete quadratic program (QP).