A Newton-CG based augmented Lagrangian method for finding a second-order stationary point of nonconvex equality constrained optimization with complexity guarantees

In this paper we consider finding a second-order stationary point (SOSP) of nonconvex equality constrained optimization when a nearly feasible point is known. In particular, we first propose a new Newton-CG method for finding an approximate SOSP of unconstrained optimization and show that it enjoys a substantially better complexity than the Newton-CG method [56]. We then propose a Newton-CG based augmented Lagrangian (AL) method for finding an approximate SOSP of nonconvex equality constrained optimization, in which the proposed Newton-CG method is used as a subproblem solver. We show that under a generalized linear independence constraint qualification (GLICQ), our AL method enjoys a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-7/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-7/2}\min\{n,\epsilon^{-3/4}\})$ for finding an $(\epsilon,\sqrt{\epsilon})$-SOSP of nonconvex equality constrained optimization with high probability, which are significantly better than the ones achieved by the proximal AL method [60]. Besides, we show that it has a total inner iteration complexity of $\widetilde{\cal O}(\epsilon^{-11/2})$ and an operation complexity of $\widetilde{\cal O}(\epsilon^{-11/2}\min\{n,\epsilon^{-5/4}\})$ when the GLICQ does not hold. To the best of our knowledge, all the complexity results obtained in this paper are new for finding an approximate SOSP of nonconvex equality constrained optimization with high probability. Preliminary numerical results also demonstrate the superiority of our proposed methods over the ones in [56,60].

Deducing Kurdyka-Łojasiewicz exponent via inf-projection

Kurdyka-{\L}ojasiewicz (KL) exponent plays an important role in estimating the convergence rate of many contemporary first-order methods. In particular, a KL exponent of $\frac12$ is related to local linear convergence. Nevertheless, KL exponent is in general extremely hard to estimate. In this paper, we show under mild assumptions that KL exponent is preserved via inf-projection. Inf-projection is a fundamental operation that is ubiquitous when reformulating optimization problems via the lift-and-project approach. By studying its operation on KL exponent, we show that the KL exponent is $\frac12$ for several important convex optimization models, including some semidefinite-programming-representable functions and functions that involve $C^2$-cone reducible structures, under conditions such as strict complementarity. Our results are applicable to concrete optimization models such as group fused Lasso and overlapping group Lasso. In addition, for nonconvex models, we show that the KL exponent of many difference-of-convex functions can be derived from that of their natural majorant functions, and the KL exponent of the Bregman envelope of a function is the same as that of the function itself. Finally, we estimate the KL exponent of the sum of the least squares function and the indicator function of the set of matrices of rank at most $k$.

A successive difference-of-convex approximation method for a class of nonconvex nonsmooth optimization problems

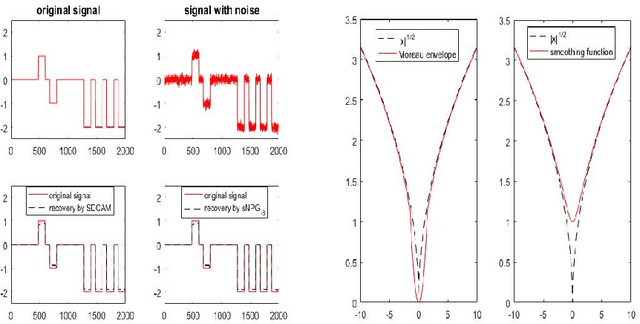
We consider a class of nonconvex nonsmooth optimization problems whose objective is the sum of a smooth function and a finite number of nonnegative proper closed possibly nonsmooth functions (whose proximal mappings are easy to compute), some of which are further composed with linear maps. This kind of problems arises naturally in various applications when different regularizers are introduced for inducing simultaneous structures in the solutions. Solving these problems, however, can be challenging because of the coupled nonsmooth functions: the corresponding proximal mapping can be hard to compute so that standard first-order methods such as the proximal gradient algorithm cannot be applied efficiently. In this paper, we propose a successive difference-of-convex approximation method for solving this kind of problems. In this algorithm, we approximate the nonsmooth functions by their Moreau envelopes in each iteration. Making use of the simple observation that Moreau envelopes of nonnegative proper closed functions are continuous {\em difference-of-convex} functions, we can then approximately minimize the approximation function by first-order methods with suitable majorization techniques. These first-order methods can be implemented efficiently thanks to the fact that the proximal mapping of {\em each} nonsmooth function is easy to compute. Under suitable assumptions, we prove that the sequence generated by our method is bounded and any accumulation point is a stationary point of the objective. We also discuss how our method can be applied to concrete applications such as nonconvex fused regularized optimization problems and simultaneously structured matrix optimization problems, and illustrate the performance numerically for these two specific applications.

A Non-monotone Alternating Updating Method for A Class of Matrix Factorization Problems

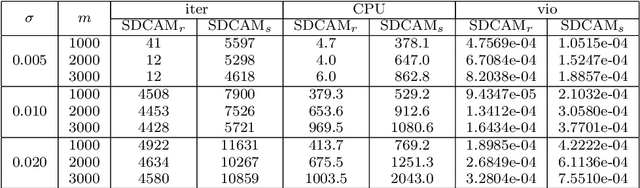
In this paper we consider a general matrix factorization model which covers a large class of existing models with many applications in areas such as machine learning and imaging sciences. To solve this possibly nonconvex, nonsmooth and non-Lipschitz problem, we develop a non-monotone alternating updating method based on a potential function. Our method essentially updates two blocks of variables in turn by inexactly minimizing this potential function, and updates another auxiliary block of variables using an explicit formula. The special structure of our potential function allows us to take advantage of efficient computational strategies for non-negative matrix factorization to perform the alternating minimization over the two blocks of variables. A suitable line search criterion is also incorporated to improve the numerical performance. Under some mild conditions, we show that the line search criterion is well defined, and establish that the sequence generated is bounded and any cluster point of the sequence is a stationary point. Finally, we conduct some numerical experiments using real datasets to compare our method with some existing efficient methods for non-negative matrix factorization and matrix completion. The numerical results show that our method can outperform these methods for these specific applications.

A refined convergence analysis of pDCA$_e$ with applications to simultaneous sparse recovery and outlier detection

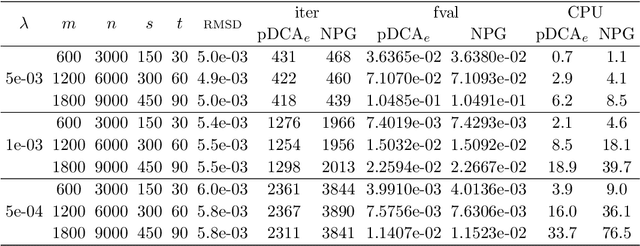
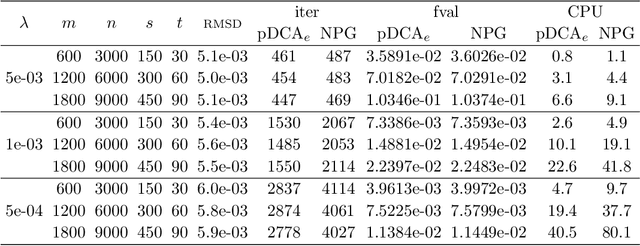
We consider the problem of minimizing a difference-of-convex (DC) function, which can be written as the sum of a smooth convex function with Lipschitz gradient, a proper closed convex function and a continuous possibly nonsmooth concave function. We refine the convergence analysis in [38] for the proximal DC algorithm with extrapolation (pDCA$_e$) and show that the whole sequence generated by the algorithm is convergent when the objective is level-bounded, {\em without} imposing differentiability assumptions in the concave part. Our analysis is based on a new potential function and we assume such a function is a Kurdyka-{\L}ojasiewicz (KL) function. We also establish a relationship between our KL assumption and the one used in [38]. Finally, we demonstrate how the pDCA$_e$ can be applied to a class of simultaneous sparse recovery and outlier detection problems arising from robust compressed sensing in signal processing and least trimmed squares regression in statistics. Specifically, we show that the objectives of these problems can be written as level-bounded DC functions whose concave parts are {\em typically nonsmooth}. Moreover, for a large class of loss functions and regularizers, the KL exponent of the corresponding potential function are shown to be 1/2, which implies that the pDCA$_e$ is locally linearly convergent when applied to these problems. Our numerical experiments show that the pDCA$_e$ usually outperforms the proximal DC algorithm with nonmonotone linesearch [24, Appendix A] in both CPU time and solution quality for this particular application.

Calculus of the exponent of Kurdyka-Łojasiewicz inequality and its applications to linear convergence of first-order methods

In this paper, we study the Kurdyka-{\L}ojasiewicz (KL) exponent, an important quantity for analyzing the convergence rate of first-order methods. Specifically, we develop various calculus rules to deduce the KL exponent of new (possibly nonconvex and nonsmooth) functions formed from functions with known KL exponents. In addition, we show that the well-studied Luo-Tseng error bound together with a mild assumption on the separation of stationary values implies that the KL exponent is $\frac12$. The Luo-Tseng error bound is known to hold for a large class of concrete structured optimization problems, and thus we deduce the KL exponent of a large class of functions whose exponents were previously unknown. Building upon this and the calculus rules, we are then able to show that for many convex or nonconvex optimization models for applications such as sparse recovery, their objective function's KL exponent is $\frac12$. This includes the least squares problem with smoothly clipped absolute deviation (SCAD) regularization or minimax concave penalty (MCP) regularization and the logistic regression problem with $\ell_1$ regularization. Since many existing local convergence rate analysis for first-order methods in the nonconvex scenario relies on the KL exponent, our results enable us to obtain explicit convergence rate for various first-order methods when they are applied to a large variety of practical optimization models. Finally, we further illustrate how our results can be applied to establishing local linear convergence of the proximal gradient algorithm and the inertial proximal algorithm with constant step-sizes for some specific models that arise in sparse recovery.

Iteratively reweighted $\ell_1$ algorithms with extrapolation

Iteratively reweighted $\ell_1$ algorithm is a popular algorithm for solving a large class of optimization problems whose objective is the sum of a Lipschitz differentiable loss function and a possibly nonconvex sparsity inducing regularizer. In this paper, motivated by the success of extrapolation techniques in accelerating first-order methods, we study how widely used extrapolation techniques such as those in [4,5,22,28] can be incorporated to possibly accelerate the iteratively reweighted $\ell_1$ algorithm. We consider three versions of such algorithms. For each version, we exhibit an explicitly checkable condition on the extrapolation parameters so that the sequence generated provably clusters at a stationary point of the optimization problem. We also investigate global convergence under additional Kurdyka-$\L$ojasiewicz assumptions on certain potential functions. Our numerical experiments show that our algorithms usually outperform the general iterative shrinkage and thresholding algorithm in [21] and an adaptation of the iteratively reweighted $\ell_1$ algorithm in [23, Algorithm 7] with nonmonotone line-search for solving random instances of log penalty regularized least squares problems in terms of both CPU time and solution quality.

Further properties of the forward-backward envelope with applications to difference-of-convex programming

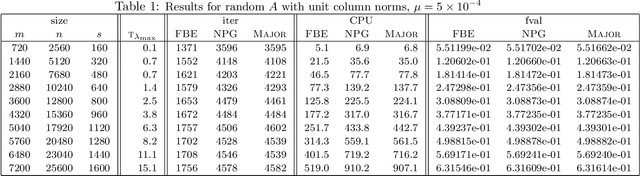
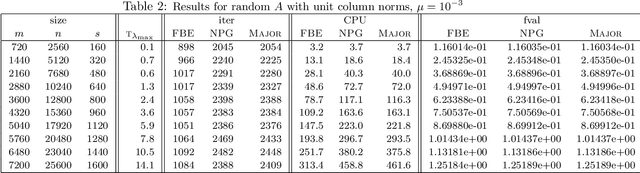
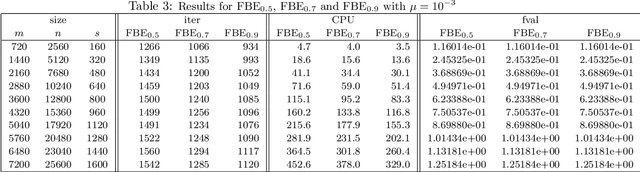
In this paper, we further study the forward-backward envelope first introduced in [28] and [30] for problems whose objective is the sum of a proper closed convex function and a twice continuously differentiable possibly nonconvex function with Lipschitz continuous gradient. We derive sufficient conditions on the original problem for the corresponding forward-backward envelope to be a level-bounded and Kurdyka-{\L}ojasiewicz function with an exponent of $\frac12$; these results are important for the efficient minimization of the forward-backward envelope by classical optimization algorithms. In addition, we demonstrate how to minimize some difference-of-convex regularized least squares problems by minimizing a suitably constructed forward-backward envelope. Our preliminary numerical results on randomly generated instances of large-scale $\ell_{1-2}$ regularized least squares problems [37] illustrate that an implementation of this approach with a limited-memory BFGS scheme usually outperforms standard first-order methods such as the nonmonotone proximal gradient method in [35].

Linear Convergence of Proximal Gradient Algorithm with Extrapolation for a Class of Nonconvex Nonsmooth Minimization Problems

In this paper, we study the proximal gradient algorithm with extrapolation for minimizing the sum of a Lipschitz differentiable function and a proper closed convex function. Under the error bound condition used in [19] for analyzing the convergence of the proximal gradient algorithm, we show that there exists a threshold such that if the extrapolation coefficients are chosen below this threshold, then the sequence generated converges $R$-linearly to a stationary point of the problem. Moreover, the corresponding sequence of objective values is also $R$-linearly convergent. In addition, the threshold reduces to $1$ for convex problems and, as a consequence, we obtain the $R$-linear convergence of the sequence generated by FISTA with fixed restart. Finally, we present some numerical experiments to illustrate our results.

Penalty methods for a class of non-Lipschitz optimization problems

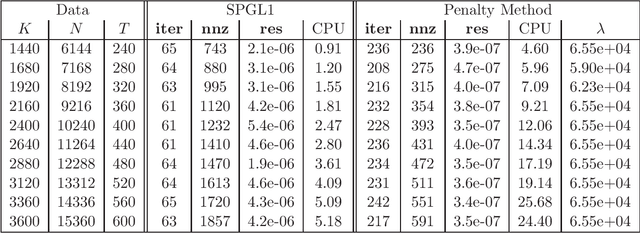
We consider a class of constrained optimization problems with a possibly nonconvex non-Lipschitz objective and a convex feasible set being the intersection of a polyhedron and a possibly degenerate ellipsoid. Such problems have a wide range of applications in data science, where the objective is used for inducing sparsity in the solutions while the constraint set models the noise tolerance and incorporates other prior information for data fitting. To solve this class of constrained optimization problems, a common approach is the penalty method. However, there is little theory on exact penalization for problems with nonconvex and non-Lipschitz objective functions. In this paper, we study the existence of exact penalty parameters regarding local minimizers, stationary points and $\epsilon$-minimizers under suitable assumptions. Moreover, we discuss a penalty method whose subproblems are solved via a nonmonotone proximal gradient method with a suitable update scheme for the penalty parameters, and prove the convergence of the algorithm to a KKT point of the constrained problem. Preliminary numerical results demonstrate the efficiency of the penalty method for finding sparse solutions of underdetermined linear systems.