Further properties of the forward-backward envelope with applications to difference-of-convex programming
Paper and Code
Oct 18, 2016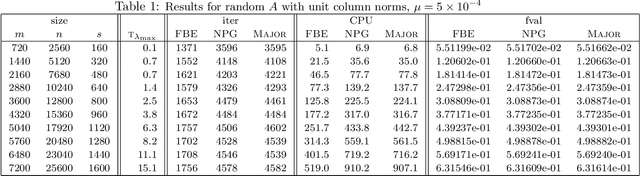
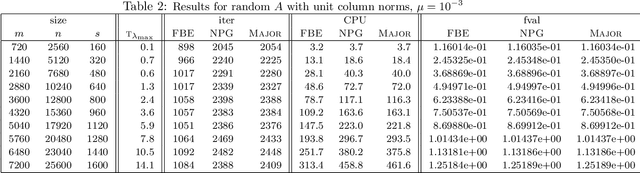
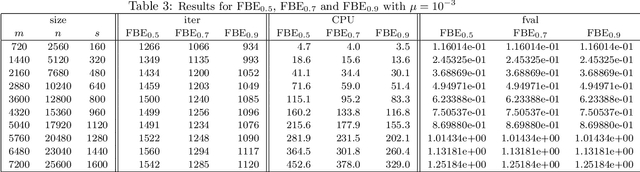

In this paper, we further study the forward-backward envelope first introduced in [28] and [30] for problems whose objective is the sum of a proper closed convex function and a twice continuously differentiable possibly nonconvex function with Lipschitz continuous gradient. We derive sufficient conditions on the original problem for the corresponding forward-backward envelope to be a level-bounded and Kurdyka-{\L}ojasiewicz function with an exponent of $\frac12$; these results are important for the efficient minimization of the forward-backward envelope by classical optimization algorithms. In addition, we demonstrate how to minimize some difference-of-convex regularized least squares problems by minimizing a suitably constructed forward-backward envelope. Our preliminary numerical results on randomly generated instances of large-scale $\ell_{1-2}$ regularized least squares problems [37] illustrate that an implementation of this approach with a limited-memory BFGS scheme usually outperforms standard first-order methods such as the nonmonotone proximal gradient method in [35].
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge