Modified K-means Algorithm with Local Optimality Guarantees

The K-means algorithm is one of the most widely studied clustering algorithms in machine learning. While extensive research has focused on its ability to achieve a globally optimal solution, there still lacks a rigorous analysis of its local optimality guarantees. In this paper, we first present conditions under which the K-means algorithm converges to a locally optimal solution. Based on this, we propose simple modifications to the K-means algorithm which ensure local optimality in both the continuous and discrete sense, with the same computational complexity as the original K-means algorithm. As the dissimilarity measure, we consider a general Bregman divergence, which is an extension of the squared Euclidean distance often used in the K-means algorithm. Numerical experiments confirm that the K-means algorithm does not always find a locally optimal solution in practice, while our proposed methods provide improved locally optimal solutions with reduced clustering loss. Our code is available at https://github.com/lmingyi/LO-K-means.

On the Role of Label Noise in the Feature Learning Process

Deep learning with noisy labels presents significant challenges. In this work, we theoretically characterize the role of label noise from a feature learning perspective. Specifically, we consider a signal-noise data distribution, where each sample comprises a label-dependent signal and label-independent noise, and rigorously analyze the training dynamics of a two-layer convolutional neural network under this data setup, along with the presence of label noise. Our analysis identifies two key stages. In Stage I, the model perfectly fits all the clean samples (i.e., samples without label noise) while ignoring the noisy ones (i.e., samples with noisy labels). During this stage, the model learns the signal from the clean samples, which generalizes well on unseen data. In Stage II, as the training loss converges, the gradient in the direction of noise surpasses that of the signal, leading to overfitting on noisy samples. Eventually, the model memorizes the noise present in the noisy samples and degrades its generalization ability. Furthermore, our analysis provides a theoretical basis for two widely used techniques for tackling label noise: early stopping and sample selection. Experiments on both synthetic and real-world setups validate our theory.

Efficient Optimization with Orthogonality Constraint: a Randomized Riemannian Submanifold Method

Optimization with orthogonality constraints frequently arises in various fields such as machine learning. Riemannian optimization offers a powerful framework for solving these problems by equipping the constraint set with a Riemannian manifold structure and performing optimization intrinsically on the manifold. This approach typically involves computing a search direction in the tangent space and updating variables via a retraction operation. However, as the size of the variables increases, the computational cost of the retraction can become prohibitively high, limiting the applicability of Riemannian optimization to large-scale problems. To address this challenge and enhance scalability, we propose a novel approach that restricts each update on a random submanifold, thereby significantly reducing the per-iteration complexity. We introduce two sampling strategies for selecting the random submanifolds and theoretically analyze the convergence of the proposed methods. We provide convergence results for general nonconvex functions and functions that satisfy Riemannian Polyak-Lojasiewicz condition as well as for stochastic optimization settings. Additionally, we demonstrate how our approach can be generalized to quotient manifolds derived from the orthogonal manifold. Extensive experiments verify the benefits of the proposed method, across a wide variety of problems.

Zeroth-Order Methods for Nonconvex Stochastic Problems with Decision-Dependent Distributions

In this study, we consider an optimization problem with uncertainty dependent on decision variables, which has recently attracted attention due to its importance in machine learning and pricing applications. In this problem, the gradient of the objective function cannot be obtained explicitly because the decision-dependent distribution is unknown. Therefore, several zeroth-order methods have been proposed, which obtain noisy objective values by sampling and update the iterates. Although these existing methods have theoretical convergence for optimization problems with decision-dependent uncertainty, they require strong assumptions about the function and distribution or exhibit large variances in their gradient estimators. To overcome these issues, we propose two zeroth-order methods under mild assumptions. First, we develop a zeroth-order method with a new one-point gradient estimator including a variance reduction parameter. The proposed method updates the decision variables while adjusting the variance reduction parameter. Second, we develop a zeroth-order method with a two-point gradient estimator. There are situations where only one-point estimators can be used, but if both one-point and two-point estimators are available, it is more practical to use the two-point estimator. As theoretical results, we show the convergence of our methods to stationary points and provide the worst-case iteration and sample complexity analysis. Our simulation experiments with real data on a retail service application show that our methods output solutions with lower objective values than the conventional zeroth-order methods.

SLTrain: a sparse plus low-rank approach for parameter and memory efficient pretraining

Large language models (LLMs) have shown impressive capabilities across various tasks. However, training LLMs from scratch requires significant computational power and extensive memory capacity. Recent studies have explored low-rank structures on weights for efficient fine-tuning in terms of parameters and memory, either through low-rank adaptation or factorization. While effective for fine-tuning, low-rank structures are generally less suitable for pretraining because they restrict parameters to a low-dimensional subspace. In this work, we propose to parameterize the weights as a sum of low-rank and sparse matrices for pretraining, which we call SLTrain. The low-rank component is learned via matrix factorization, while for the sparse component, we employ a simple strategy of uniformly selecting the sparsity support at random and learning only the non-zero entries with the fixed support. While being simple, the random fixed-support sparse learning strategy significantly enhances pretraining when combined with low-rank learning. Our results show that SLTrain adds minimal extra parameters and memory costs compared to pretraining with low-rank parameterization, yet achieves substantially better performance, which is comparable to full-rank training. Remarkably, when combined with quantization and per-layer updates, SLTrain can reduce memory requirements by up to 73% when pretraining the LLaMA 7B model.

A Framework for Bilevel Optimization on Riemannian Manifolds

Bilevel optimization has seen an increasing presence in various domains of applications. In this work, we propose a framework for solving bilevel optimization problems where variables of both lower and upper level problems are constrained on Riemannian manifolds. We provide several hypergradient estimation strategies on manifolds and study their estimation error. We provide convergence and complexity analysis for the proposed hypergradient descent algorithm on manifolds. We also extend the developments to stochastic bilevel optimization and to the use of general retraction. We showcase the utility of the proposed framework on various applications.

Convergence Error Analysis of Reflected Gradient Langevin Dynamics for Globally Optimizing Non-Convex Constrained Problems

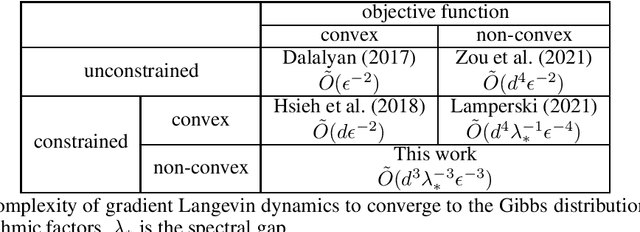
Non-convex optimization problems have various important applications, whereas many algorithms have been proven only to converge to stationary points. Meanwhile, gradient Langevin dynamics (GLD) and its variants have attracted increasing attention as a framework to provide theoretical convergence guarantees for a global solution in non-convex settings. The studies on GLD initially treated unconstrained convex problems and very recently expanded to convex constrained non-convex problems by Lamperski (2021). In this work, we can deal with non-convex problems with some kind of non-convex feasible region. This work analyzes reflected gradient Langevin dynamics (RGLD), a global optimization algorithm for smoothly constrained problems, including non-convex constrained ones, and derives a convergence rate to a solution with $\epsilon$-sampling error. The convergence rate is faster than the one given by Lamperski (2021) for convex constrained cases. Our proofs exploit the Poisson equation to effectively utilize the reflection for the faster convergence rate.

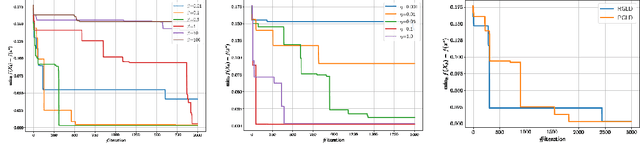
A Gradient Method for Multilevel Optimization

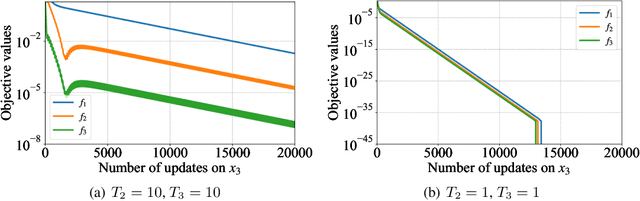
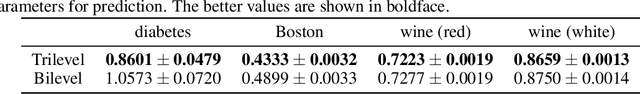
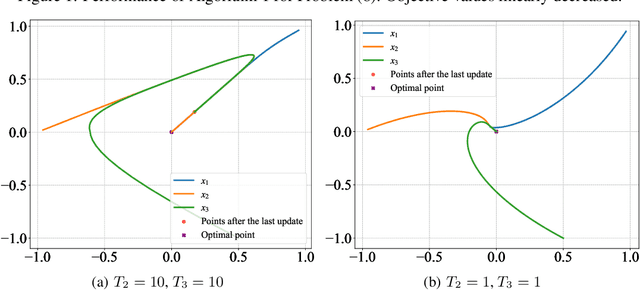
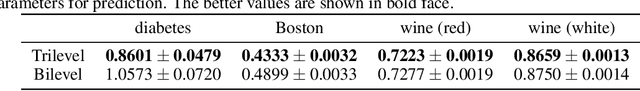
Although application examples of multilevel optimization have already been discussed since the '90s, the development of solution methods was almost limited to bilevel cases due to the difficulty of the problem. In recent years, in machine learning, Franceschi et al. have proposed a method for solving bilevel optimization problems by replacing their lower-level problems with the $T$ steepest descent update equations with some prechosen iteration number $T$. In this paper, we have developed a gradient-based algorithm for multilevel optimization with $n$ levels based on their idea and proved that our reformulation with $n T$ variables asymptotically converges to the original multilevel problem. As far as we know, this is one of the first algorithms with some theoretical guarantee for multilevel optimization. Numerical experiments show that a trilevel hyperparameter learning model considering data poisoning produces more stable prediction results than an existing bilevel hyperparameter learning model in noisy data settings.

BODAME: Bilevel Optimization for Defense Against Model Extraction

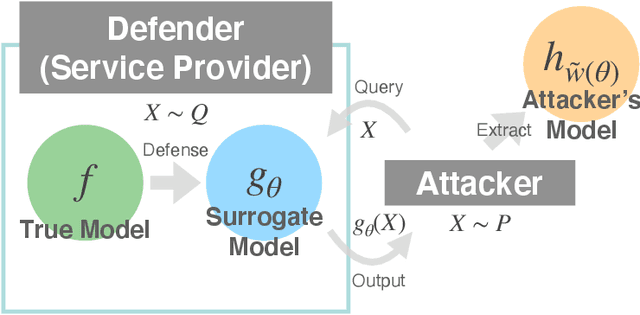
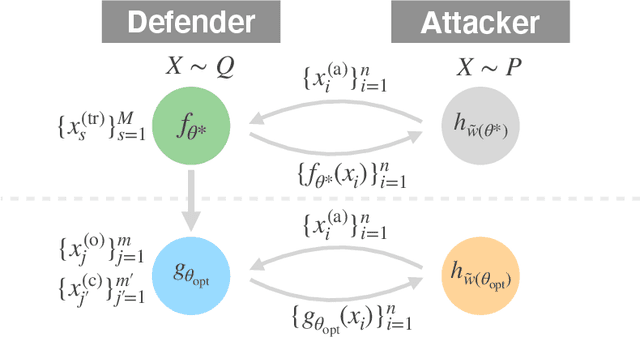
Model extraction attacks have become serious issues for service providers using machine learning. We consider an adversarial setting to prevent model extraction under the assumption that attackers will make their best guess on the service provider's model using query accesses, and propose to build a surrogate model that significantly keeps away the predictions of the attacker's model from those of the true model. We formulate the problem as a non-convex constrained bilevel optimization problem and show that for kernel models, it can be transformed into a non-convex 1-quadratically constrained quadratic program with a polynomial-time algorithm to find the global optimum. Moreover, we give a tractable transformation and an algorithm for more complicated models that are learned by using stochastic gradient descent-based algorithms. Numerical experiments show that the surrogate model performs well compared with existing defense models when the difference between the attacker's and service provider's distributions is large. We also empirically confirm the generalization ability of the surrogate model.

Theory and Algorithms for Shapelet-based Multiple-Instance Learning

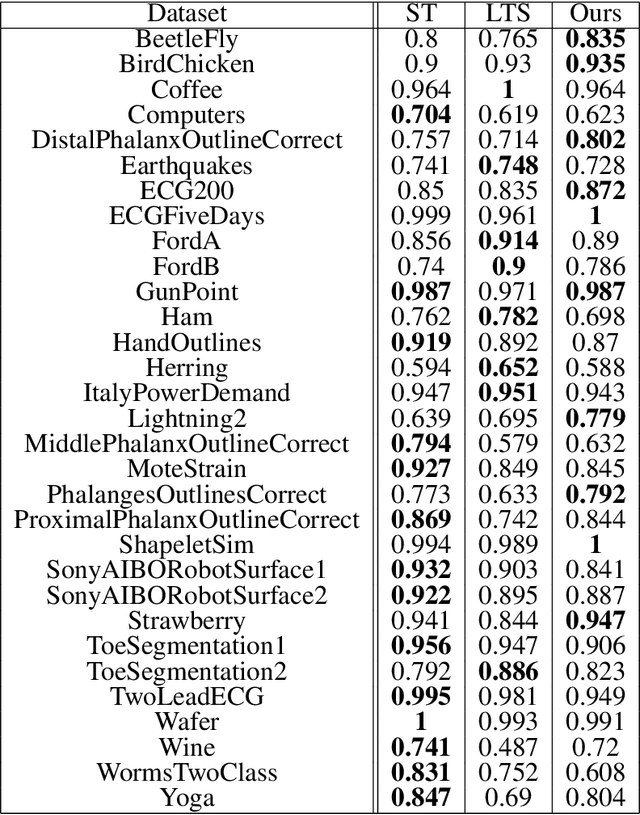
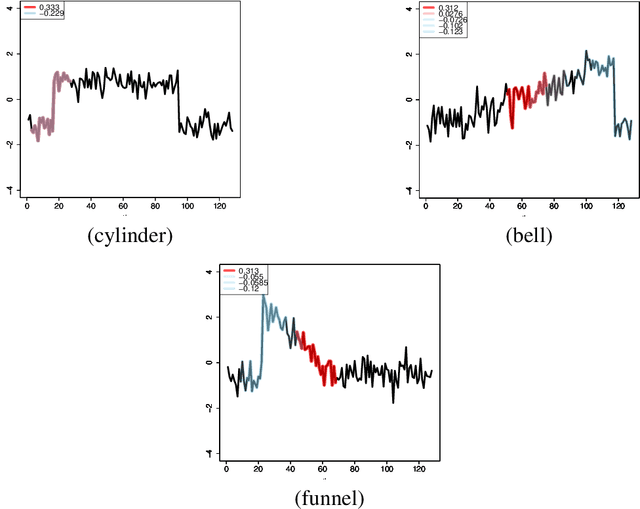
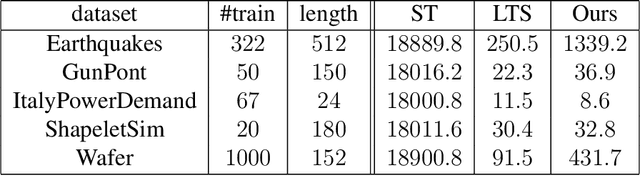
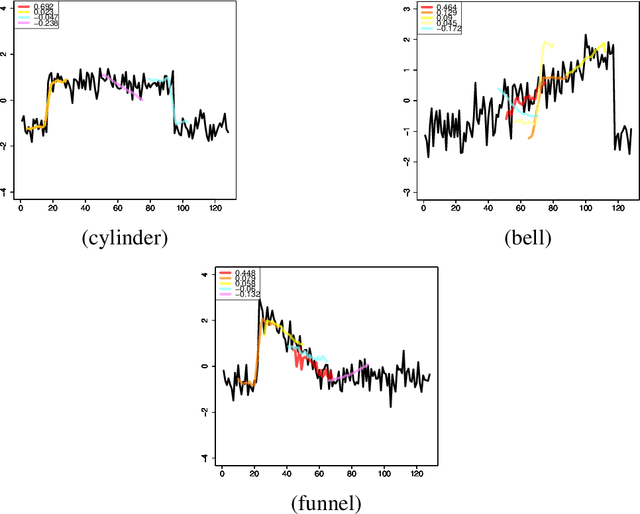
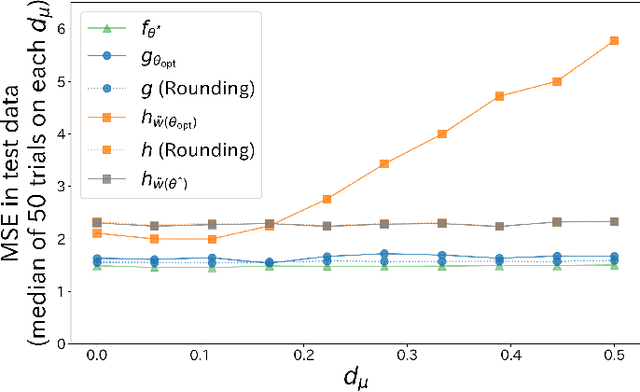
We propose a new formulation of Multiple-Instance Learning (MIL), in which a unit of data consists of a set of instances called a bag. The goal is to find a good classifier of bags based on the similarity with a "shapelet" (or pattern), where the similarity of a bag with a shapelet is the maximum similarity of instances in the bag. In previous work, some of the training instances are chosen as shapelets with no theoretical justification. In our formulation, we use all possible, and thus infinitely many shapelets, resulting in a richer class of classifiers. We show that the formulation is tractable, that is, it can be reduced through Linear Programming Boosting (LPBoost) to Difference of Convex (DC) programs of finite (actually polynomial) size. Our theoretical result also gives justification to the heuristics of some of the previous work. The time complexity of the proposed algorithm highly depends on the size of the set of all instances in the training sample. To apply to the data containing a large number of instances, we also propose a heuristic option of the algorithm without the loss of the theoretical guarantee. Our empirical study demonstrates that our algorithm uniformly works for Shapelet Learning tasks on time-series classification and various MIL tasks with comparable accuracy to the existing methods. Moreover, we show that the proposed heuristics allow us to achieve the result with reasonable computational time.