Shuji Yamamoto
Theory and Algorithms for Shapelet-based Multiple-Instance Learning
Jun 12, 2020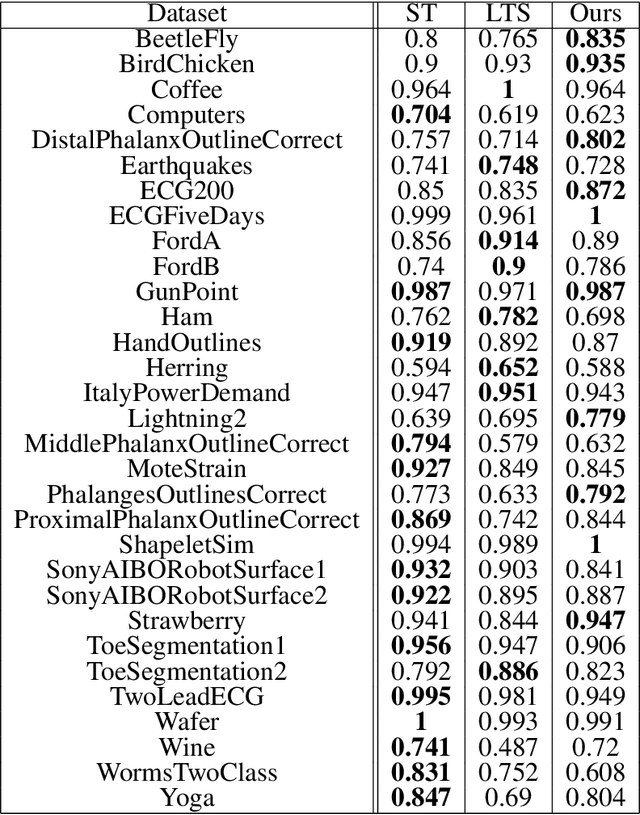
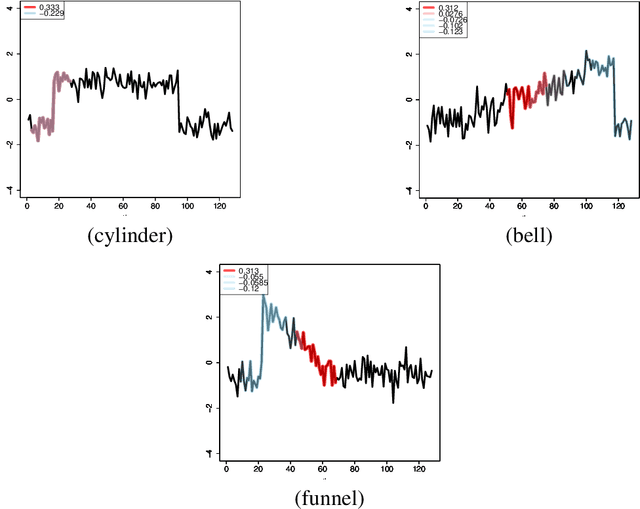
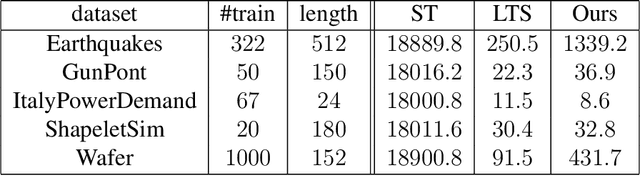
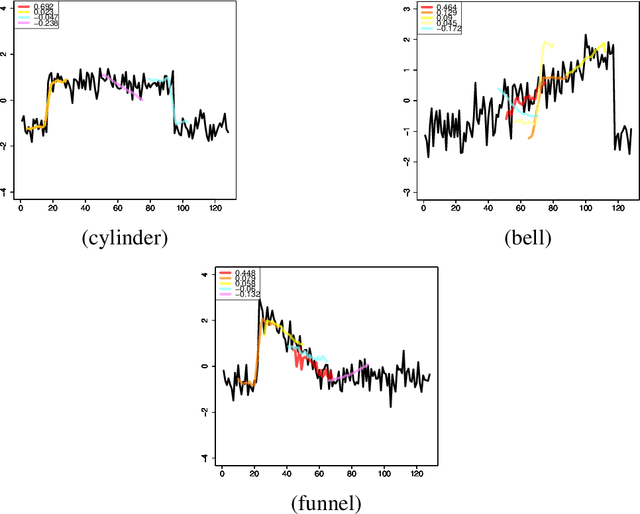
Abstract:We propose a new formulation of Multiple-Instance Learning (MIL), in which a unit of data consists of a set of instances called a bag. The goal is to find a good classifier of bags based on the similarity with a "shapelet" (or pattern), where the similarity of a bag with a shapelet is the maximum similarity of instances in the bag. In previous work, some of the training instances are chosen as shapelets with no theoretical justification. In our formulation, we use all possible, and thus infinitely many shapelets, resulting in a richer class of classifiers. We show that the formulation is tractable, that is, it can be reduced through Linear Programming Boosting (LPBoost) to Difference of Convex (DC) programs of finite (actually polynomial) size. Our theoretical result also gives justification to the heuristics of some of the previous work. The time complexity of the proposed algorithm highly depends on the size of the set of all instances in the training sample. To apply to the data containing a large number of instances, we also propose a heuristic option of the algorithm without the loss of the theoretical guarantee. Our empirical study demonstrates that our algorithm uniformly works for Shapelet Learning tasks on time-series classification and various MIL tasks with comparable accuracy to the existing methods. Moreover, we show that the proposed heuristics allow us to achieve the result with reasonable computational time.
Multiple-Instance Learning by Boosting Infinitely Many Shapelet-based Classifiers
Dec 10, 2018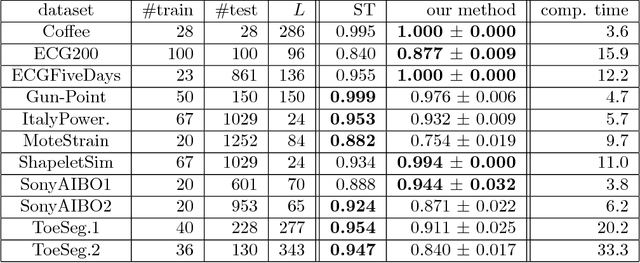

Abstract:We propose a new formulation of Multiple-Instance Learning (MIL). In typical MIL settings, a unit of data is given as a set of instances called a bag and the goal is to find a good classifier of bags based on similarity from a single or finitely many "shapelets" (or patterns), where the similarity of the bag from a shapelet is the maximum similarity of instances in the bag. Classifiers based on a single shapelet are not sufficiently strong for certain applications. Additionally, previous work with multiple shapelets has heuristically chosen some of the instances as shapelets with no theoretical guarantee of its generalization ability. Our formulation provides a richer class of the final classifiers based on infinitely many shapelets. We provide an efficient algorithm for the new formulation, in addition to generalization bound. Our empirical study demonstrates that our approach is effective not only for MIL tasks but also for Shapelet Learning for time-series classification.
Boosting the kernelized shapelets: Theory and algorithms for local features
Sep 07, 2017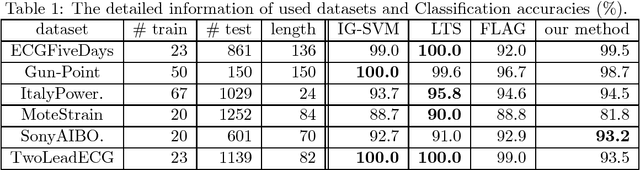
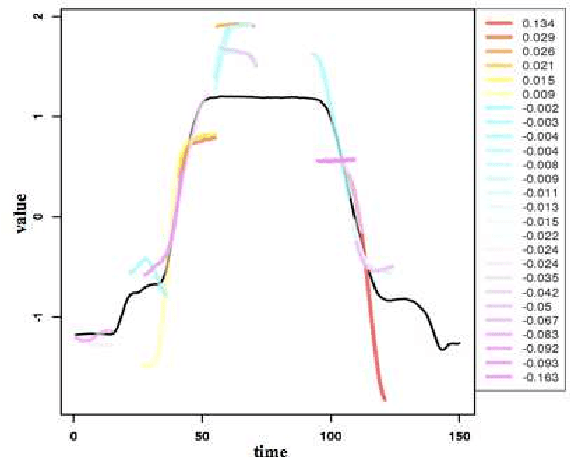
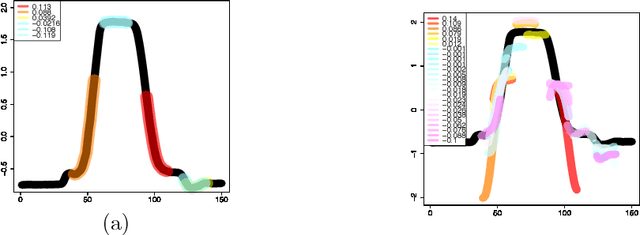
Abstract:We consider binary classification problems using local features of objects. One of motivating applications is time-series classification, where features reflecting some local closeness measure between a time series and a pattern sequence called shapelet are useful. Despite the empirical success of such approaches using local features, the generalization ability of resulting hypotheses is not fully understood and previous work relies on a bunch of heuristics. In this paper, we formulate a class of hypotheses using local features, where the richness of features is controlled by kernels. We derive generalization bounds of sparse ensembles over the class which is exponentially better than a standard analysis in terms of the number of possible local features. The resulting optimization problem is well suited to the boosting approach and the weak learning problem is formulated as a DC program, for which practical algorithms exist. In preliminary experiments on time-series data sets, our method achieves competitive accuracy with the state-of-the-art algorithms with small parameter-tuning cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge