Boosting the kernelized shapelets: Theory and algorithms for local features
Paper and Code
Sep 07, 2017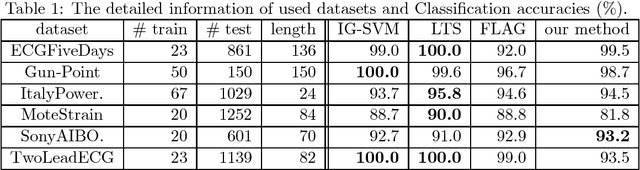
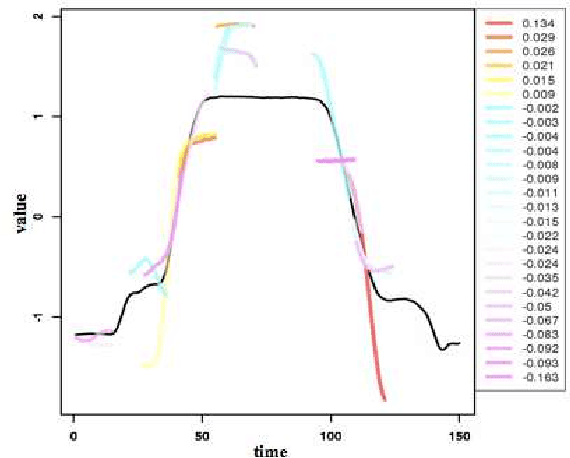
We consider binary classification problems using local features of objects. One of motivating applications is time-series classification, where features reflecting some local closeness measure between a time series and a pattern sequence called shapelet are useful. Despite the empirical success of such approaches using local features, the generalization ability of resulting hypotheses is not fully understood and previous work relies on a bunch of heuristics. In this paper, we formulate a class of hypotheses using local features, where the richness of features is controlled by kernels. We derive generalization bounds of sparse ensembles over the class which is exponentially better than a standard analysis in terms of the number of possible local features. The resulting optimization problem is well suited to the boosting approach and the weak learning problem is formulated as a DC program, for which practical algorithms exist. In preliminary experiments on time-series data sets, our method achieves competitive accuracy with the state-of-the-art algorithms with small parameter-tuning cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge