Convergence Error Analysis of Reflected Gradient Langevin Dynamics for Globally Optimizing Non-Convex Constrained Problems

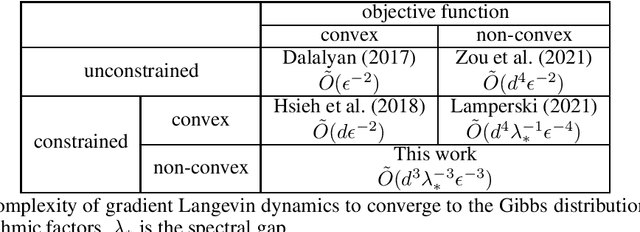
Non-convex optimization problems have various important applications, whereas many algorithms have been proven only to converge to stationary points. Meanwhile, gradient Langevin dynamics (GLD) and its variants have attracted increasing attention as a framework to provide theoretical convergence guarantees for a global solution in non-convex settings. The studies on GLD initially treated unconstrained convex problems and very recently expanded to convex constrained non-convex problems by Lamperski (2021). In this work, we can deal with non-convex problems with some kind of non-convex feasible region. This work analyzes reflected gradient Langevin dynamics (RGLD), a global optimization algorithm for smoothly constrained problems, including non-convex constrained ones, and derives a convergence rate to a solution with $\epsilon$-sampling error. The convergence rate is faster than the one given by Lamperski (2021) for convex constrained cases. Our proofs exploit the Poisson equation to effectively utilize the reflection for the faster convergence rate.