Intrinsic Muon: Spectral Optimization on Riemannian Matrix Manifolds

Muon and related norm-constrained matrix optimizers have become central to large-scale learning problems. They are formulated as a linear maximization oracle (LMO) over an ambient matrix-norm ball in unconstrained Euclidean space. However, these do not generalize cleanly to manifold-valued parameters such as low-rank factorizations, orthogonality constraints, or symmetric positive definite (SPD) matrices. Naively restricting the Muon LMO to the tangent space (i) breaks quotient symmetries and (ii) couples the tangent-space constraint with an ambient norm bound, thereby obstructing closed-form solutions on various manifolds of interest. We resolve both issues with a single observation: every Riemannian metric canonically lifts a unitarily invariant Euclidean norm to an intrinsic norm on each tangent space, and the resulting intrinsic norm constrained LMO is symmetry preserving. Building on this, we introduce intrinsic Muon (iMuon), a unified framework that yields closed-form updates on the fixed-rank, SPD, Stiefel, and Grassmann manifolds for any unitarily invariant norm, including the spectral, Frobenius, and nuclear norms. We establish convergence guarantees for both deterministic and stochastic iMuon with rate constants that depend only on the manifold dimension. Notably, on the fixed-rank manifold this constant depends only on the rank, making the rate independent of factor conditioning and removing the runtime factor-rescaling required by prior work. Experiments on LoRA finetuning of LLMs, image classification, and subspace learning illustrate the efficacy of the proposed approach.

Contrastive Identification and Generation in the Limit

In the classical identification in the limit model of Gold [1967], a stream of positive examples is presented round by round, and the learner must eventually recover the target hypothesis. Recently, Kleinberg and Mullainathan [2024] introduced generation in the limit, where the learner instead must eventually output novel elements of the target's support. Both lines of work focus on positive-only or fully labeled data. Yet many natural supervision signals are inherently relational rather than singleton, which encode relationships between examples rather than labels of individual ones. We initiate the study of contrastive identification and generation in the limit, where the learner observes a contrastive presentation of data: a stream of unordered pairs $\{x,y\}$ satisfying $h(x)\ne h(y)$ for an unknown target binary hypothesis $h$, but which element is positive is hidden from the learner. We first present three results in the noiseless setting: an exact characterization of contrastive identifiable classes (a one-line geometric refinement of Angluin [1980]'s tell-tale condition), a combinatorial dimension called contrastive closure dimension (a contrasitive analogue of the closure dimension in Raman et al. [2025]) and exactly characterizing uniform contrastive generation with tight sample complexity, and a strict hierarchy in which contrastive generation and text identification are mutually incomparable. We then prove a sharp reversal under finite adversarial corruption: there exist classes identifiable from contrastive pairs under any finite corruption budget by a single budget-independent algorithm, yet not identifiable from positive examples under even one corrupted observation. The unifying technical object is the common crossing graph, which encodes pairwise ambiguity, family-level generation obstructions, and corruption defects in a single coverage-and-incidence language.

DPRM: A Plug-in Doob h transform-induced Token-Ordering Module for Diffusion Language Models

Diffusion language models generate without a fixed left-to-right order, making token ordering a central algorithmic choice: which tokens should be revealed, retained, revised or verified at each step? Existing systems mainly use random masking or confidence-driven ordering. Random masking creates train--test mismatch, while confidence-only rules are efficient but can be myopic and suppress useful exploration. We introduce DPRM (Doob h-transform Process Reward Model), a plug-in token-ordering module for diffusion language models. DPRM keeps the host architecture, denoising objective and supervision unchanged, and changes only the ordering policy. It starts from confidence-driven progressive ordering and gradually shifts to Doob h transform Process Reward guided ordering through online estimates. We characterize the exact DPRM policy as a reward-tilted Gibbs reveal law, prove O(1/N) convergence of the stagewise Soft-BoN approximation, and show that the online bucketized controller tracks the exact DPRM score at empirical-Bernstein rates. Under tractable optimization assumptions, DPRM also yields a sample-complexity advantage over random and confidence-only ordering. DPRM improves over confidence-based baselines in pretraining, post-training, test-time scaling, and single-cell masked diffusion, with particularly strong gains on harder reasoning subsets. In protein, molecular generation and DNA design, the effect is more multi-objective: ordering-aware variants significantly improve selected structural or fragment-constrained metrics while not uniformly dominating the host baseline on every quality metric. These results identify token ordering as a fundamental control axis in diffusion language models and establish DPRM as a general-purpose module for improving it. Code is available at https://github.com/DakeBU/DPRM-DLLM.

On the Price of Privacy for Language Identification and Generation

As large language models (LLMs) are increasingly trained on sensitive user data, understanding the fundamental cost of privacy in language learning becomes essential. We initiate the study of differentially private (DP) language identification and generation in the agnostic statistical setting, establishing algorithms and matching lower bounds that precisely quantify the cost of privacy. For both tasks, approximate $(\varepsilon, δ)$-DP with constant $\varepsilon > 0$ recovers the non-private error rates: $\exp(-r(n))$ for identification (for any $r(n) = o(n)$) and $\exp(-Ω(n))$ for generation. Under pure $\varepsilon$-DP, the exponents degrade by a multiplicative factor of $\min\{1, \varepsilon\}$, which we show is tight up to constants. Notably, for generation under pure DP with mild assumptions, the upper bound $\exp(-\min\{1,\varepsilon\} \cdot Ω(n))$ matches the lower bound up to some constants, establishing an optimal rate. Our results show that the cost of privacy in language learning is surprisingly mild: absent entirely under approximate DP, and exactly a $\min\{1,\varepsilon\}$ factor in the exponent under pure DP.

On the Learning Dynamics of Two-layer Linear Networks with Label Noise SGD

One crucial factor behind the success of deep learning lies in the implicit bias induced by noise inherent in gradient-based training algorithms. Motivated by empirical observations that training with noisy labels improves model generalization, we delve into the underlying mechanisms behind stochastic gradient descent (SGD) with label noise. Focusing on a two-layer over-parameterized linear network, we analyze the learning dynamics of label noise SGD, unveiling a two-phase learning behavior. In \emph{Phase I}, the magnitudes of model weights progressively diminish, and the model escapes the lazy regime; enters the rich regime. In \emph{Phase II}, the alignment between model weights and the ground-truth interpolator increases, and the model eventually converges. Our analysis highlights the critical role of label noise in driving the transition from the lazy to the rich regime and minimally explains its empirical success. Furthermore, we extend these insights to Sharpness-Aware Minimization (SAM), showing that the principles governing label noise SGD also apply to broader optimization algorithms. Extensive experiments, conducted under both synthetic and real-world setups, strongly support our theory. Our code is released at https://github.com/a-usually/Label-Noise-SGD.

Wiener Chaos Expansion based Neural Operator for Singular Stochastic Partial Differential Equations

In this paper, we explore how our recently developed Wiener Chaos Expansion (WCE)-based neural operator (NO) can be applied to singular stochastic partial differential equations, e.g., the dynamic $\boldsymbolΦ^4_2$ model simulated in the recent works. Unlike the previous WCE-NO which solves SPDEs by simply inserting Wick-Hermite features into the backbone NO model, we leverage feature-wise linear modulation (FiLM) to appropriately capture the dependency between the solution of singular SPDE and its smooth remainder. The resulting WCE-FiLM-NO shows excellent performance on $\boldsymbolΦ^4_2$, as measured by relative $L_2$ loss, out-of-distribution $L_2$ loss, and autocorrelation score; all without the help of renormalisation factor. In addition, we also show the potential of simulating $\boldsymbolΦ^4_3$ data, which is more aligned with real scientific practice in statistical quantum field theory. To the best of our knowledge, this is among the first works to develop an efficient data-driven surrogate for the dynamical $\boldsymbolΦ^4_3$ model.

Expanding the Chaos: Neural Operator for Stochastic (Partial) Differential Equations

Stochastic differential equations (SDEs) and stochastic partial differential equations (SPDEs) are fundamental tools for modeling stochastic dynamics across the natural sciences and modern machine learning. Developing deep learning models for approximating their solution operators promises not only fast, practical solvers, but may also inspire models that resolve classical learning tasks from a new perspective. In this work, we build on classical Wiener chaos expansions (WCE) to design neural operator (NO) architectures for SPDEs and SDEs: we project the driving noise paths onto orthonormal Wick Hermite features and parameterize the resulting deterministic chaos coefficients with neural operators, so that full solution trajectories can be reconstructed from noise in a single forward pass. On the theoretical side, we investigate the classical WCE results for the class of multi-dimensional SDEs and semilinear SPDEs considered here by explicitly writing down the associated coupled ODE/PDE systems for their chaos coefficients, which makes the separation between stochastic forcing and deterministic dynamics fully explicit and directly motivates our model designs. On the empirical side, we validate our models on a diverse suite of problems: classical SPDE benchmarks, diffusion one-step sampling on images, topological interpolation on graphs, financial extrapolation, parameter estimation, and manifold SDEs for flood prediction, demonstrating competitive accuracy and broad applicability. Overall, our results indicate that WCE-based neural operators provide a practical and scalable way to learn SDE/SPDE solution operators across diverse domains.

ACT as Human: Multimodal Large Language Model Data Annotation with Critical Thinking

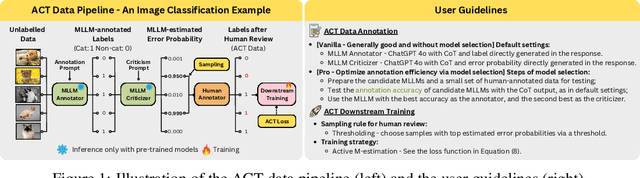
Supervised learning relies on high-quality labeled data, but obtaining such data through human annotation is both expensive and time-consuming. Recent work explores using large language models (LLMs) for annotation, but LLM-generated labels still fall short of human-level quality. To address this problem, we propose the Annotation with Critical Thinking (ACT) data pipeline, where LLMs serve not only as annotators but also as judges to critically identify potential errors. Human effort is then directed towards reviewing only the most "suspicious" cases, significantly improving the human annotation efficiency. Our major contributions are as follows: (1) ACT is applicable to a wide range of domains, including natural language processing (NLP), computer vision (CV), and multimodal understanding, by leveraging multimodal-LLMs (MLLMs). (2) Through empirical studies, we derive 7 insights on how to enhance annotation quality while efficiently reducing the human cost, and then translate these findings into user-friendly guidelines. (3) We theoretically analyze how to modify the loss function so that models trained on ACT data achieve similar performance to those trained on fully human-annotated data. Our experiments show that the performance gap can be reduced to less than 2% on most benchmark datasets while saving up to 90% of human costs.

Generalized infinite dimensional Alpha-Procrustes based geometries

This work extends the recently introduced Alpha-Procrustes family of Riemannian metrics for symmetric positive definite (SPD) matrices by incorporating generalized versions of the Bures-Wasserstein (GBW), Log-Euclidean, and Wasserstein distances. While the Alpha-Procrustes framework has unified many classical metrics in both finite- and infinite- dimensional settings, it previously lacked the structural components necessary to realize these generalized forms. We introduce a formalism based on unitized Hilbert-Schmidt operators and an extended Mahalanobis norm that allows the construction of robust, infinite-dimensional generalizations of GBW and Log-Hilbert-Schmidt distances. Our approach also incorporates a learnable regularization parameter that enhances geometric stability in high-dimensional comparisons. Preliminary experiments reproducing benchmarks from the literature demonstrate the improved performance of our generalized metrics, particularly in scenarios involving comparisons between datasets of varying dimension and scale. This work lays a theoretical and computational foundation for advancing robust geometric methods in machine learning, statistical inference, and functional data analysis.

Consistency Is Not Always Correct: Towards Understanding the Role of Exploration in Post-Training Reasoning

Foundation models exhibit broad knowledge but limited task-specific reasoning, motivating post-training strategies such as RLVR and inference scaling with outcome or process reward models (ORM/PRM). While recent work highlights the role of exploration and entropy stability in improving pass@K, empirical evidence points to a paradox: RLVR and ORM/PRM typically reinforce existing tree-like reasoning paths rather than expanding the reasoning scope, raising the question of why exploration helps at all if no new patterns emerge. To reconcile this paradox, we adopt the perspective of Kim et al. (2025), viewing easy (e.g., simplifying a fraction) versus hard (e.g., discovering a symmetry) reasoning steps as low- versus high-probability Markov transitions, and formalize post-training dynamics through Multi-task Tree-structured Markov Chains (TMC). In this tractable model, pretraining corresponds to tree expansion, while post-training corresponds to chain-of-thought reweighting. We show that several phenomena recently observed in empirical studies arise naturally in this setting: (1) RLVR induces a squeezing effect, reducing reasoning entropy and forgetting some correct paths; (2) population rewards of ORM/PRM encourage consistency rather than accuracy, thereby favoring common patterns; and (3) certain rare, high-uncertainty reasoning paths by the base model are responsible for solving hard problem instances. Together, these explain why exploration -- even when confined to the base model's reasoning scope -- remains essential: it preserves access to rare but crucial reasoning traces needed for difficult cases, which are squeezed out by RLVR or unfavored by inference scaling. Building on this, we further show that exploration strategies such as rejecting easy instances and KL regularization help preserve rare reasoning traces. Empirical simulations corroborate our theoretical results.