SMART: Semantic Matching Contrastive Learning for Partially View-Aligned Clustering

Multi-view clustering has been empirically shown to improve learning performance by leveraging the inherent complementary information across multiple views of data. However, in real-world scenarios, collecting strictly aligned views is challenging, and learning from both aligned and unaligned data becomes a more practical solution. Partially View-aligned Clustering aims to learn correspondences between misaligned view samples to better exploit the potential consistency and complementarity across views, including both aligned and unaligned data. However, most existing PVC methods fail to leverage unaligned data to capture the shared semantics among samples from the same cluster. Moreover, the inherent heterogeneity of multi-view data induces distributional shifts in representations, leading to inaccuracies in establishing meaningful correspondences between cross-view latent features and, consequently, impairing learning effectiveness. To address these challenges, we propose a Semantic MAtching contRasTive learning model (SMART) for PVC. The main idea of our approach is to alleviate the influence of cross-view distributional shifts, thereby facilitating semantic matching contrastive learning to fully exploit semantic relationships in both aligned and unaligned data. Extensive experiments on eight benchmark datasets demonstrate that our method consistently outperforms existing approaches on the PVC problem.

Refinement Contrastive Learning of Cell-Gene Associations for Unsupervised Cell Type Identification

Unsupervised cell type identification is crucial for uncovering and characterizing heterogeneous populations in single cell omics studies. Although a range of clustering methods have been developed, most focus exclusively on intrinsic cellular structure and ignore the pivotal role of cell-gene associations, which limits their ability to distinguish closely related cell types. To this end, we propose a Refinement Contrastive Learning framework (scRCL) that explicitly incorporates cell-gene interactions to derive more informative representations. Specifically, we introduce two contrastive distribution alignment components that reveal reliable intrinsic cellular structures by effectively exploiting cell-cell structural relationships. Additionally, we develop a refinement module that integrates gene-correlation structure learning to enhance cell embeddings by capturing underlying cell-gene associations. This module strengthens connections between cells and their associated genes, refining the representation learning to exploiting biologically meaningful relationships. Extensive experiments on several single-cell RNA-seq and spatial transcriptomics benchmark datasets demonstrate that our method consistently outperforms state-of-the-art baselines in cell-type identification accuracy. Moreover, downstream biological analyses confirm that the recovered cell populations exhibit coherent gene-expression signatures, further validating the biological relevance of our approach. The code is available at https://github.com/THPengL/scRCL.

Consistency Is Not Always Correct: Towards Understanding the Role of Exploration in Post-Training Reasoning

Foundation models exhibit broad knowledge but limited task-specific reasoning, motivating post-training strategies such as RLVR and inference scaling with outcome or process reward models (ORM/PRM). While recent work highlights the role of exploration and entropy stability in improving pass@K, empirical evidence points to a paradox: RLVR and ORM/PRM typically reinforce existing tree-like reasoning paths rather than expanding the reasoning scope, raising the question of why exploration helps at all if no new patterns emerge. To reconcile this paradox, we adopt the perspective of Kim et al. (2025), viewing easy (e.g., simplifying a fraction) versus hard (e.g., discovering a symmetry) reasoning steps as low- versus high-probability Markov transitions, and formalize post-training dynamics through Multi-task Tree-structured Markov Chains (TMC). In this tractable model, pretraining corresponds to tree expansion, while post-training corresponds to chain-of-thought reweighting. We show that several phenomena recently observed in empirical studies arise naturally in this setting: (1) RLVR induces a squeezing effect, reducing reasoning entropy and forgetting some correct paths; (2) population rewards of ORM/PRM encourage consistency rather than accuracy, thereby favoring common patterns; and (3) certain rare, high-uncertainty reasoning paths by the base model are responsible for solving hard problem instances. Together, these explain why exploration -- even when confined to the base model's reasoning scope -- remains essential: it preserves access to rare but crucial reasoning traces needed for difficult cases, which are squeezed out by RLVR or unfavored by inference scaling. Building on this, we further show that exploration strategies such as rejecting easy instances and KL regularization help preserve rare reasoning traces. Empirical simulations corroborate our theoretical results.

Provable Benefit of Curriculum in Transformer Tree-Reasoning Post-Training

Recent curriculum techniques in the post-training stage of LLMs have been widely observed to outperform non-curriculum approaches in enhancing reasoning performance, yet a principled understanding of why and to what extent they work remains elusive. To address this gap, we develop a theoretical framework grounded in the intuition that progressively learning through manageable steps is more efficient than directly tackling a hard reasoning task, provided each stage stays within the model's effective competence. Under mild complexity conditions linking consecutive curriculum stages, we show that curriculum post-training avoids the exponential complexity bottleneck. To substantiate this result, drawing insights from the Chain-of-Thoughts (CoTs) solving mathematical problems such as Countdown and parity, we model CoT generation as a states-conditioned autoregressive reasoning tree, define a uniform-branching base model to capture pretrained behavior, and formalize curriculum stages as either depth-increasing (longer reasoning chains) or hint-decreasing (shorter prefixes) subtasks. Our analysis shows that, under outcome-only reward signals, reinforcement learning finetuning achieves high accuracy with polynomial sample complexity, whereas direct learning suffers from an exponential bottleneck. We further establish analogous guarantees for test-time scaling, where curriculum-aware querying reduces both reward oracle calls and sampling cost from exponential to polynomial order.

Model Adaptation: Unsupervised Domain Adaptation without Source Data

In this paper, we investigate a challenging unsupervised domain adaptation setting -- unsupervised model adaptation. We aim to explore how to rely only on unlabeled target data to improve performance of an existing source prediction model on the target domain, since labeled source data may not be available in some real-world scenarios due to data privacy issues. For this purpose, we propose a new framework, which is referred to as collaborative class conditional generative adversarial net to bypass the dependence on the source data. Specifically, the prediction model is to be improved through generated target-style data, which provides more accurate guidance for the generator. As a result, the generator and the prediction model can collaborate with each other without source data. Furthermore, due to the lack of supervision from source data, we propose a weight constraint that encourages similarity to the source model. A clustering-based regularization is also introduced to produce more discriminative features in the target domain. Compared to conventional domain adaptation methods, our model achieves superior performance on multiple adaptation tasks with only unlabeled target data, which verifies its effectiveness in this challenging setting.

Discrete Prior-based Temporal-coherent Content Prediction for Blind Face Video Restoration

Blind face video restoration aims to restore high-fidelity details from videos subjected to complex and unknown degradations. This task poses a significant challenge of managing temporal heterogeneity while at the same time maintaining stable face attributes. In this paper, we introduce a Discrete Prior-based Temporal-Coherent content prediction transformer to address the challenge, and our model is referred to as DP-TempCoh. Specifically, we incorporate a spatial-temporal-aware content prediction module to synthesize high-quality content from discrete visual priors, conditioned on degraded video tokens. To further enhance the temporal coherence of the predicted content, a motion statistics modulation module is designed to adjust the content, based on discrete motion priors in terms of cross-frame mean and variance. As a result, the statistics of the predicted content can match with that of real videos over time. By performing extensive experiments, we verify the effectiveness of the design elements and demonstrate the superior performance of our DP-TempCoh in both synthetically and naturally degraded video restoration.

Provably Transformers Harness Multi-Concept Word Semantics for Efficient In-Context Learning

Transformer-based large language models (LLMs) have displayed remarkable creative prowess and emergence capabilities. Existing empirical studies have revealed a strong connection between these LLMs' impressive emergence abilities and their in-context learning (ICL) capacity, allowing them to solve new tasks using only task-specific prompts without further fine-tuning. On the other hand, existing empirical and theoretical studies also show that there is a linear regularity of the multi-concept encoded semantic representation behind transformer-based LLMs. However, existing theoretical work fail to build up an understanding of the connection between this regularity and the innovative power of ICL. Additionally, prior work often focuses on simplified, unrealistic scenarios involving linear transformers or unrealistic loss functions, and they achieve only linear or sub-linear convergence rates. In contrast, this work provides a fine-grained mathematical analysis to show how transformers leverage the multi-concept semantics of words to enable powerful ICL and excellent out-of-distribution ICL abilities, offering insights into how transformers innovate solutions for certain unseen tasks encoded with multiple cross-concept semantics. Inspired by empirical studies on the linear latent geometry of LLMs, the analysis is based on a concept-based low-noise sparse coding prompt model. Leveraging advanced techniques, this work showcases the exponential 0-1 loss convergence over the highly non-convex training dynamics, which pioneeringly incorporates the challenges of softmax self-attention, ReLU-activated MLPs, and cross-entropy loss. Empirical simulations corroborate the theoretical findings.

Provably Neural Active Learning Succeeds via Prioritizing Perplexing Samples

Neural Network-based active learning (NAL) is a cost-effective data selection technique that utilizes neural networks to select and train on a small subset of samples. While existing work successfully develops various effective or theory-justified NAL algorithms, the understanding of the two commonly used query criteria of NAL: uncertainty-based and diversity-based, remains in its infancy. In this work, we try to move one step forward by offering a unified explanation for the success of both query criteria-based NAL from a feature learning view. Specifically, we consider a feature-noise data model comprising easy-to-learn or hard-to-learn features disrupted by noise, and conduct analysis over 2-layer NN-based NALs in the pool-based scenario. We provably show that both uncertainty-based and diversity-based NAL are inherently amenable to one and the same principle, i.e., striving to prioritize samples that contain yet-to-be-learned features. We further prove that this shared principle is the key to their success-achieve small test error within a small labeled set. Contrastingly, the strategy-free passive learning exhibits a large test error due to the inadequate learning of yet-to-be-learned features, necessitating resort to a significantly larger label complexity for a sufficient test error reduction. Experimental results validate our findings.

Towards a Mathematical Foundation of Immunology and Amino Acid Chains

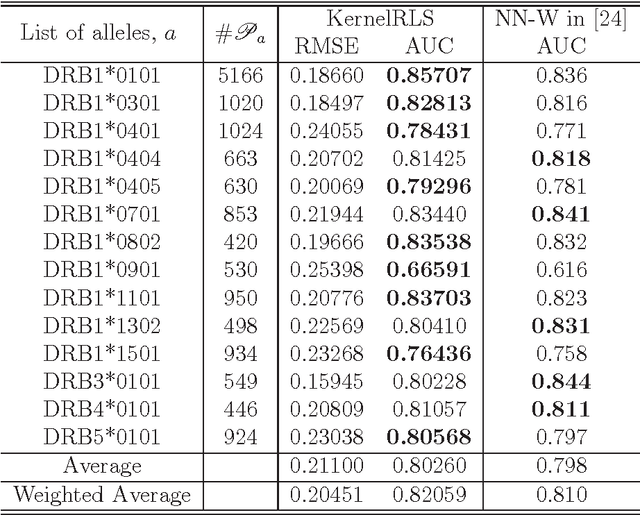
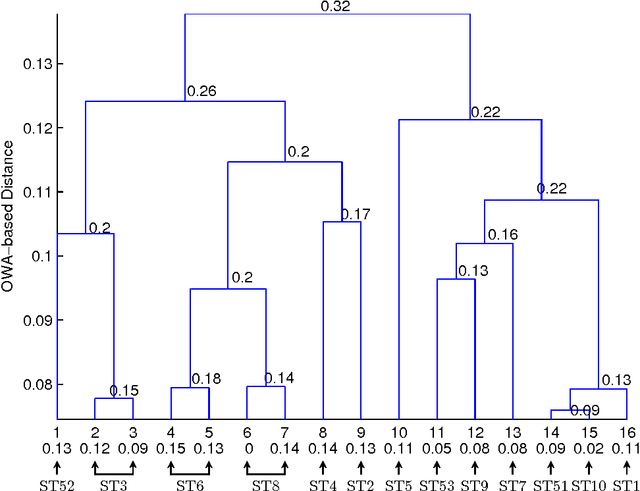
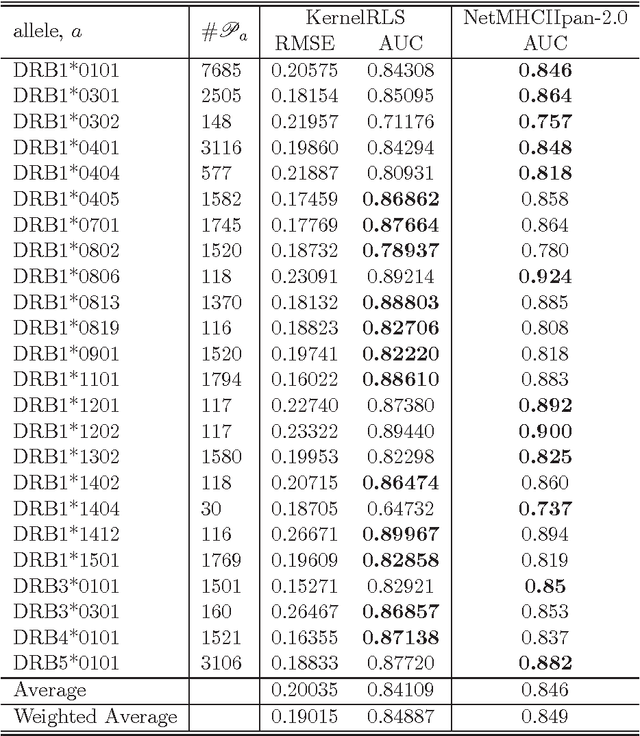
We attempt to set a mathematical foundation of immunology and amino acid chains. To measure the similarities of these chains, a kernel on strings is defined using only the sequence of the chains and a good amino acid substitution matrix (e.g. BLOSUM62). The kernel is used in learning machines to predict binding affinities of peptides to human leukocyte antigens DR (HLA-DR) molecules. On both fixed allele (Nielsen and Lund 2009) and pan-allele (Nielsen et.al. 2010) benchmark databases, our algorithm achieves the state-of-the-art performance. The kernel is also used to define a distance on an HLA-DR allele set based on which a clustering analysis precisely recovers the serotype classifications assigned by WHO (Nielsen and Lund 2009, and Marsh et.al. 2010). These results suggest that our kernel relates well the chain structure of both peptides and HLA-DR molecules to their biological functions, and that it offers a simple, powerful and promising methodology to immunology and amino acid chain studies.