An Introduction to Bi-level Optimization: Foundations and Applications in Signal Processing and Machine Learning

Recently, bi-level optimization (BLO) has taken center stage in some very exciting developments in the area of signal processing (SP) and machine learning (ML). Roughly speaking, BLO is a classical optimization problem that involves two levels of hierarchy (i.e., upper and lower levels), wherein obtaining the solution to the upper-level problem requires solving the lower-level one. BLO has become popular largely because it is powerful in modeling problems in SP and ML, among others, that involve optimizing nested objective functions. Prominent applications of BLO range from resource allocation for wireless systems to adversarial machine learning. In this work, we focus on a class of tractable BLO problems that often appear in SP and ML applications. We provide an overview of some basic concepts of this class of BLO problems, such as their optimality conditions, standard algorithms (including their optimization principles and practical implementations), as well as how they can be leveraged to obtain state-of-the-art results for a number of key SP and ML applications. Further, we discuss some recent advances in BLO theory, its implications for applications, and point out some limitations of the state-of-the-art that require significant future research efforts. Overall, we hope that this article can serve to accelerate the adoption of BLO as a generic tool to model, analyze, and innovate on a wide array of emerging SP and ML applications.

Zeroth-Order SciML: Non-intrusive Integration of Scientific Software with Deep Learning

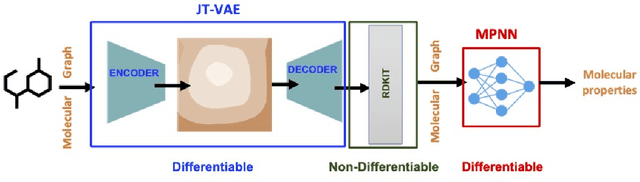
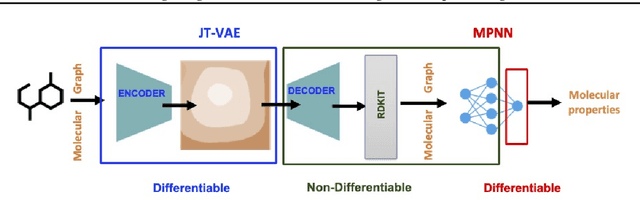
Using deep learning (DL) to accelerate and/or improve scientific workflows can yield discoveries that are otherwise impossible. Unfortunately, DL models have yielded limited success in complex scientific domains due to large data requirements. In this work, we propose to overcome this issue by integrating the abundance of scientific knowledge sources (SKS) with the DL training process. Existing knowledge integration approaches are limited to using differentiable knowledge source to be compatible with first-order DL training paradigm. In contrast, our proposed approach treats knowledge source as a black-box in turn allowing to integrate virtually any knowledge source. To enable an end-to-end training of SKS-coupled-DL, we propose to use zeroth-order optimization (ZOO) based gradient-free training schemes, which is non-intrusive, i.e., does not require making any changes to the SKS. We evaluate the performance of our ZOO training scheme on two real-world material science applications. We show that proposed scheme is able to effectively integrate scientific knowledge with DL training and is able to outperform purely data-driven model for data-limited scientific applications. We also discuss some limitations of the proposed method and mention potentially worthwhile future directions.

Hybrid Block Successive Approximation for One-Sided Non-Convex Min-Max Problems: Algorithms and Applications

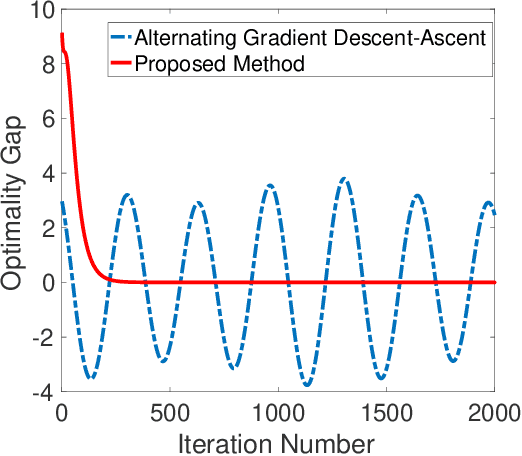
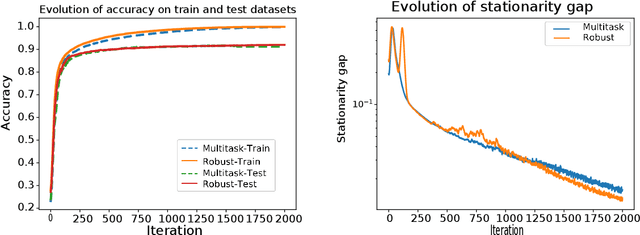
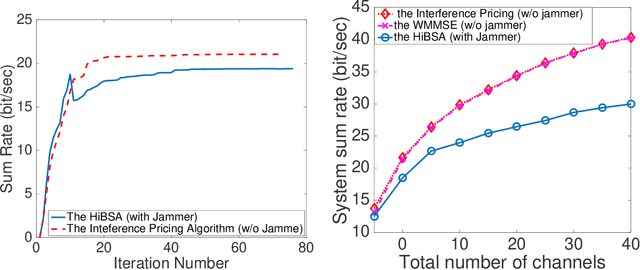
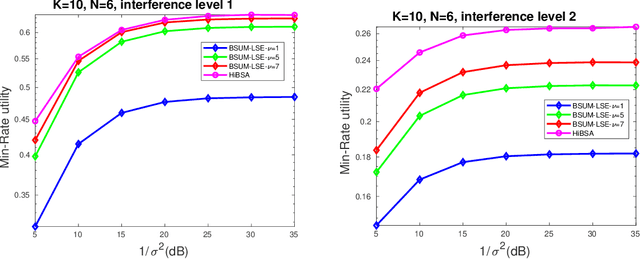
The min-max problem, also known as the saddle point problem, is a class of optimization problems in which we minimize and maximize two subsets of variables simultaneously. This class of problems can be used to formulate a wide range of signal processing and communication (SPCOM) problems. Despite its popularity, existing theory for this class has been mainly developed for problems with certain special convex-concave structure. Therefore, it cannot be used to guide the algorithm design for many interesting problems in SPCOM, where some kind of non-convexity often arises. In this work, we consider a general block-wise one-sided non-convex min-max problem, in which the minimization problem consists of multiple blocks and is non-convex, while the maximization problem is (strongly) concave. We propose a class of simple algorithms named Hybrid Block Successive Approximation (HiBSA), which alternatingly performs gradient descent-type steps for the minimization blocks and one gradient ascent-type step for the maximization problem. A key element in the proposed algorithm is the introduction of certain properly designed regularization and penalty terms, which are used to stabilize the algorithm and ensure convergence. For the first time, we show that such simple alternating min-max algorithms converge to first-order stationary solutions, with quantifiable global rates. To validate the efficiency of the proposed algorithms, we conduct numerical tests on a number of information processing and wireless communication problems, including the robust learning problem, the non-convex min-utility maximization problems, and certain wireless jamming problem arising in interfering channels.