Hybrid Block Successive Approximation for One-Sided Non-Convex Min-Max Problems: Algorithms and Applications

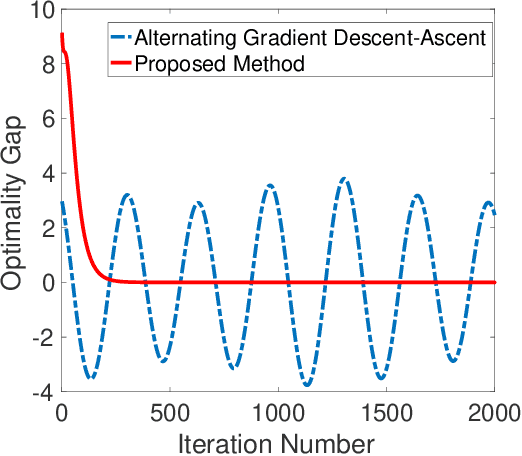
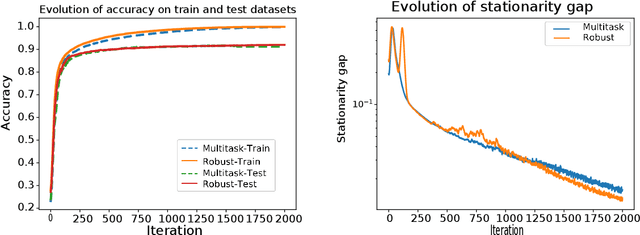
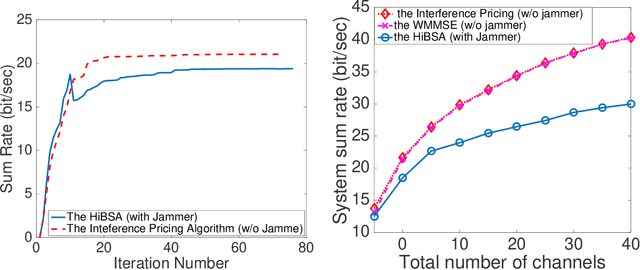
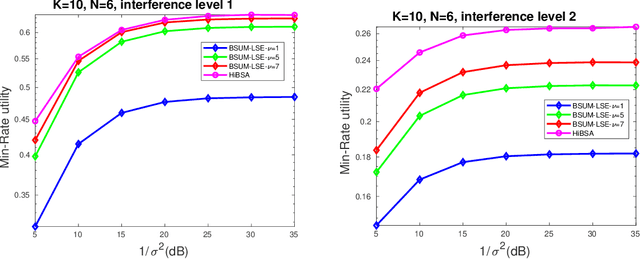
The min-max problem, also known as the saddle point problem, is a class of optimization problems in which we minimize and maximize two subsets of variables simultaneously. This class of problems can be used to formulate a wide range of signal processing and communication (SPCOM) problems. Despite its popularity, existing theory for this class has been mainly developed for problems with certain special convex-concave structure. Therefore, it cannot be used to guide the algorithm design for many interesting problems in SPCOM, where some kind of non-convexity often arises. In this work, we consider a general block-wise one-sided non-convex min-max problem, in which the minimization problem consists of multiple blocks and is non-convex, while the maximization problem is (strongly) concave. We propose a class of simple algorithms named Hybrid Block Successive Approximation (HiBSA), which alternatingly performs gradient descent-type steps for the minimization blocks and one gradient ascent-type step for the maximization problem. A key element in the proposed algorithm is the introduction of certain properly designed regularization and penalty terms, which are used to stabilize the algorithm and ensure convergence. For the first time, we show that such simple alternating min-max algorithms converge to first-order stationary solutions, with quantifiable global rates. To validate the efficiency of the proposed algorithms, we conduct numerical tests on a number of information processing and wireless communication problems, including the robust learning problem, the non-convex min-utility maximization problems, and certain wireless jamming problem arising in interfering channels.