Dai Shi
Expanding the Chaos: Neural Operator for Stochastic (Partial) Differential Equations
Jan 03, 2026Abstract:Stochastic differential equations (SDEs) and stochastic partial differential equations (SPDEs) are fundamental tools for modeling stochastic dynamics across the natural sciences and modern machine learning. Developing deep learning models for approximating their solution operators promises not only fast, practical solvers, but may also inspire models that resolve classical learning tasks from a new perspective. In this work, we build on classical Wiener chaos expansions (WCE) to design neural operator (NO) architectures for SPDEs and SDEs: we project the driving noise paths onto orthonormal Wick Hermite features and parameterize the resulting deterministic chaos coefficients with neural operators, so that full solution trajectories can be reconstructed from noise in a single forward pass. On the theoretical side, we investigate the classical WCE results for the class of multi-dimensional SDEs and semilinear SPDEs considered here by explicitly writing down the associated coupled ODE/PDE systems for their chaos coefficients, which makes the separation between stochastic forcing and deterministic dynamics fully explicit and directly motivates our model designs. On the empirical side, we validate our models on a diverse suite of problems: classical SPDE benchmarks, diffusion one-step sampling on images, topological interpolation on graphs, financial extrapolation, parameter estimation, and manifold SDEs for flood prediction, demonstrating competitive accuracy and broad applicability. Overall, our results indicate that WCE-based neural operators provide a practical and scalable way to learn SDE/SPDE solution operators across diverse domains.
ACT as Human: Multimodal Large Language Model Data Annotation with Critical Thinking
Nov 13, 2025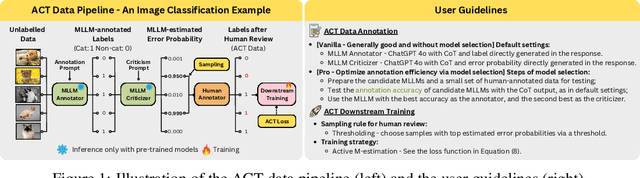



Abstract:Supervised learning relies on high-quality labeled data, but obtaining such data through human annotation is both expensive and time-consuming. Recent work explores using large language models (LLMs) for annotation, but LLM-generated labels still fall short of human-level quality. To address this problem, we propose the Annotation with Critical Thinking (ACT) data pipeline, where LLMs serve not only as annotators but also as judges to critically identify potential errors. Human effort is then directed towards reviewing only the most "suspicious" cases, significantly improving the human annotation efficiency. Our major contributions are as follows: (1) ACT is applicable to a wide range of domains, including natural language processing (NLP), computer vision (CV), and multimodal understanding, by leveraging multimodal-LLMs (MLLMs). (2) Through empirical studies, we derive 7 insights on how to enhance annotation quality while efficiently reducing the human cost, and then translate these findings into user-friendly guidelines. (3) We theoretically analyze how to modify the loss function so that models trained on ACT data achieve similar performance to those trained on fully human-annotated data. Our experiments show that the performance gap can be reduced to less than 2% on most benchmark datasets while saving up to 90% of human costs.
MAGI-1: Autoregressive Video Generation at Scale
May 19, 2025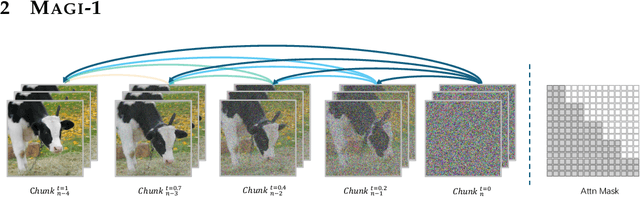
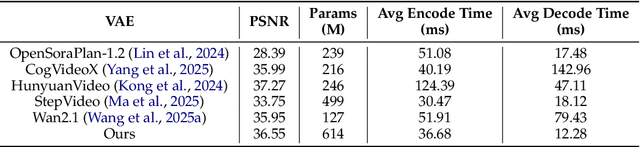
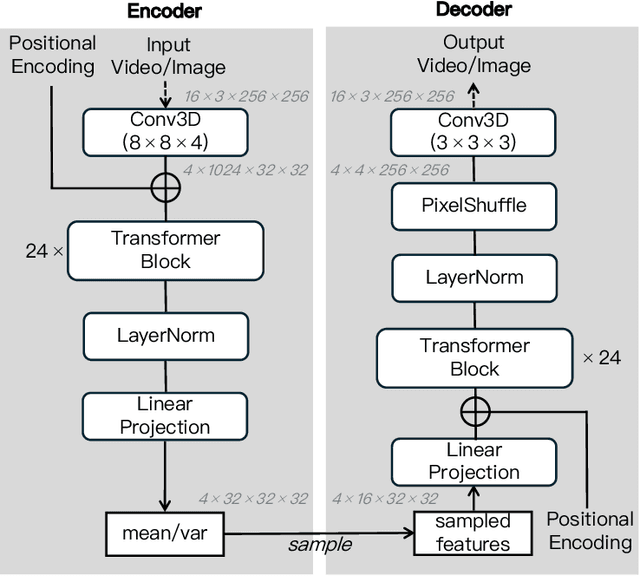
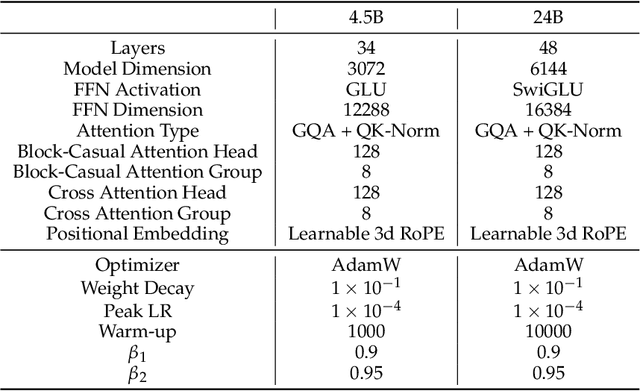
Abstract:We present MAGI-1, a world model that generates videos by autoregressively predicting a sequence of video chunks, defined as fixed-length segments of consecutive frames. Trained to denoise per-chunk noise that increases monotonically over time, MAGI-1 enables causal temporal modeling and naturally supports streaming generation. It achieves strong performance on image-to-video (I2V) tasks conditioned on text instructions, providing high temporal consistency and scalability, which are made possible by several algorithmic innovations and a dedicated infrastructure stack. MAGI-1 facilitates controllable generation via chunk-wise prompting and supports real-time, memory-efficient deployment by maintaining constant peak inference cost, regardless of video length. The largest variant of MAGI-1 comprises 24 billion parameters and supports context lengths of up to 4 million tokens, demonstrating the scalability and robustness of our approach. The code and models are available at https://github.com/SandAI-org/MAGI-1 and https://github.com/SandAI-org/MagiAttention. The product can be accessed at https://sand.ai.
Graph Pseudotime Analysis and Neural Stochastic Differential Equations for Analyzing Retinal Degeneration Dynamics and Beyond
Feb 10, 2025Abstract:Understanding disease progression at the molecular pathway level usually requires capturing both structural dependencies between pathways and the temporal dynamics of disease evolution. In this work, we solve the former challenge by developing a biologically informed graph-forming method to efficiently construct pathway graphs for subjects from our newly curated JR5558 mouse transcriptomics dataset. We then develop Graph-level Pseudotime Analysis (GPA) to infer graph-level trajectories that reveal how disease progresses at the population level, rather than in individual subjects. Based on the trajectories estimated by GPA, we identify the most sensitive pathways that drive disease stage transitions. In addition, we measure changes in pathway features using neural stochastic differential equations (SDEs), which enables us to formally define and compute pathway stability and disease bifurcation points (points of no return), two fundamental problems in disease progression research. We further extend our theory to the case when pathways can interact with each other, enabling a more comprehensive and multi-faceted characterization of disease phenotypes. The comprehensive experimental results demonstrate the effectiveness of our framework in reconstructing the dynamics of the pathway, identifying critical transitions, and providing novel insights into the mechanistic understanding of disease evolution.
When Graph Neural Networks Meet Dynamic Mode Decomposition
Oct 08, 2024



Abstract:Graph Neural Networks (GNNs) have emerged as fundamental tools for a wide range of prediction tasks on graph-structured data. Recent studies have drawn analogies between GNN feature propagation and diffusion processes, which can be interpreted as dynamical systems. In this paper, we delve deeper into this perspective by connecting the dynamics in GNNs to modern Koopman theory and its numerical method, Dynamic Mode Decomposition (DMD). We illustrate how DMD can estimate a low-rank, finite-dimensional linear operator based on multiple states of the system, effectively approximating potential nonlinear interactions between nodes in the graph. This approach allows us to capture complex dynamics within the graph accurately and efficiently. We theoretically establish a connection between the DMD-estimated operator and the original dynamic operator between system states. Building upon this foundation, we introduce a family of DMD-GNN models that effectively leverage the low-rank eigenfunctions provided by the DMD algorithm. We further discuss the potential of enhancing our approach by incorporating domain-specific constraints such as symmetry into the DMD computation, allowing the corresponding GNN models to respect known physical properties of the underlying system. Our work paves the path for applying advanced dynamical system analysis tools via GNNs. We validate our approach through extensive experiments on various learning tasks, including directed graphs, large-scale graphs, long-range interactions, and spatial-temporal graphs. We also empirically verify that our proposed models can serve as powerful encoders for link prediction tasks. The results demonstrate that our DMD-enhanced GNNs achieve state-of-the-art performance, highlighting the effectiveness of integrating DMD into GNN frameworks.
Diffusing to the Top: Boost Graph Neural Networks with Minimal Hyperparameter Tuning
Oct 08, 2024



Abstract:Graph Neural Networks (GNNs) are proficient in graph representation learning and achieve promising performance on versatile tasks such as node classification and link prediction. Usually, a comprehensive hyperparameter tuning is essential for fully unlocking GNN's top performance, especially for complicated tasks such as node classification on large graphs and long-range graphs. This is usually associated with high computational and time costs and careful design of appropriate search spaces. This work introduces a graph-conditioned latent diffusion framework (GNN-Diff) to generate high-performing GNNs based on the model checkpoints of sub-optimal hyperparameters selected by a light-tuning coarse search. We validate our method through 166 experiments across four graph tasks: node classification on small, large, and long-range graphs, as well as link prediction. Our experiments involve 10 classic and state-of-the-art target models and 20 publicly available datasets. The results consistently demonstrate that GNN-Diff: (1) boosts the performance of GNNs with efficient hyperparameter tuning; and (2) presents high stability and generalizability on unseen data across multiple generation runs. The code is available at https://github.com/lequanlin/GNN-Diff.
A Riemannian Approach to Ground Metric Learning for Optimal Transport
Sep 16, 2024Abstract:Optimal transport (OT) theory has attracted much attention in machine learning and signal processing applications. OT defines a notion of distance between probability distributions of source and target data points. A crucial factor that influences OT-based distances is the ground metric of the embedding space in which the source and target data points lie. In this work, we propose to learn a suitable latent ground metric parameterized by a symmetric positive definite matrix. We use the rich Riemannian geometry of symmetric positive definite matrices to jointly learn the OT distance along with the ground metric. Empirical results illustrate the efficacy of the learned metric in OT-based domain adaptation.
Machine Learning-Based Prediction of Key Genes Correlated to the Subretinal Lesion Severity in a Mouse Model of Age-Related Macular Degeneration
Sep 08, 2024



Abstract:Age-related macular degeneration (AMD) is a major cause of blindness in older adults, severely affecting vision and quality of life. Despite advances in understanding AMD, the molecular factors driving the severity of subretinal scarring (fibrosis) remain elusive, hampering the development of effective therapies. This study introduces a machine learning-based framework to predict key genes that are strongly correlated with lesion severity and to identify potential therapeutic targets to prevent subretinal fibrosis in AMD. Using an original RNA sequencing (RNA-seq) dataset from the diseased retinas of JR5558 mice, we developed a novel and specific feature engineering technique, including pathway-based dimensionality reduction and gene-based feature expansion, to enhance prediction accuracy. Two iterative experiments were conducted by leveraging Ridge and ElasticNet regression models to assess biological relevance and gene impact. The results highlight the biological significance of several key genes and demonstrate the framework's effectiveness in identifying novel therapeutic targets. The key findings provide valuable insights for advancing drug discovery efforts and improving treatment strategies for AMD, with the potential to enhance patient outcomes by targeting the underlying genetic mechanisms of subretinal lesion development.
Unleash Graph Neural Networks from Heavy Tuning
May 21, 2024



Abstract:Graph Neural Networks (GNNs) are deep-learning architectures designed for graph-type data, where understanding relationships among individual observations is crucial. However, achieving promising GNN performance, especially on unseen data, requires comprehensive hyperparameter tuning and meticulous training. Unfortunately, these processes come with high computational costs and significant human effort. Additionally, conventional searching algorithms such as grid search may result in overfitting on validation data, diminishing generalization accuracy. To tackle these challenges, we propose a graph conditional latent diffusion framework (GNN-Diff) to generate high-performing GNNs directly by learning from checkpoints saved during a light-tuning coarse search. Our method: (1) unleashes GNN training from heavy tuning and complex search space design; (2) produces GNN parameters that outperform those obtained through comprehensive grid search; and (3) establishes higher-quality generation for GNNs compared to diffusion frameworks designed for general neural networks.
Design Your Own Universe: A Physics-Informed Agnostic Method for Enhancing Graph Neural Networks
Feb 05, 2024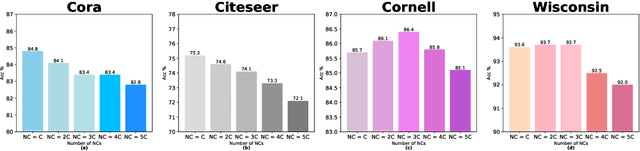
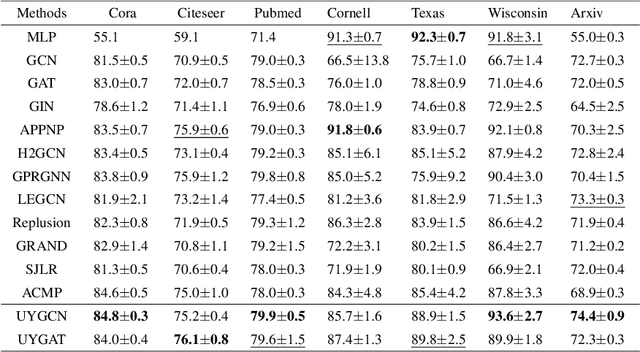
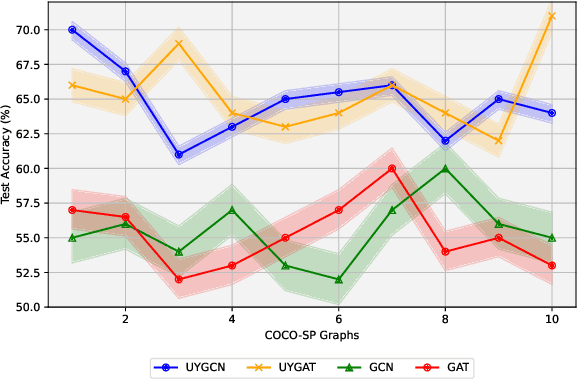
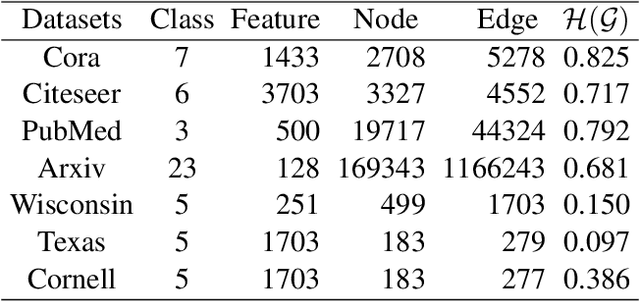
Abstract:Physics-informed Graph Neural Networks have achieved remarkable performance in learning through graph-structured data by mitigating common GNN challenges such as over-smoothing, over-squashing, and heterophily adaption. Despite these advancements, the development of a simple yet effective paradigm that appropriately integrates previous methods for handling all these challenges is still underway. In this paper, we draw an analogy between the propagation of GNNs and particle systems in physics, proposing a model-agnostic enhancement framework. This framework enriches the graph structure by introducing additional nodes and rewiring connections with both positive and negative weights, guided by node labeling information. We theoretically verify that GNNs enhanced through our approach can effectively circumvent the over-smoothing issue and exhibit robustness against over-squashing. Moreover, we conduct a spectral analysis on the rewired graph to demonstrate that the corresponding GNNs can fit both homophilic and heterophilic graphs. Empirical validations on benchmarks for homophilic, heterophilic graphs, and long-term graph datasets show that GNNs enhanced by our method significantly outperform their original counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge